3. Уравнение плоскости по трем точкам:

В векторном виде:

В координатах: 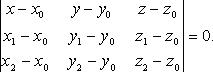или

4. Уравнение плоскости по точке и двум неколлинеарным векторам

В векторном виде:

В координатах:

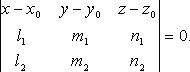
5. Общее уравнение: Ax+By+Cz+D=0

Билет 26. Прямая и плоскость.

Всякое уравнение первой степени относительно координат x, y, z

Ax + By + Cz +D = 0, задает плоскость, и наоборот: всякая плоскость может быть представлена данным уравнением, которое называется уравнением плоскости.

Вектор n (A, B, C ), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении коэффициенты A, B, C одновременно не равны 0.

Особые случаи уравнения плоскости:

1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.

2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.

3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.

4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей: x = 0, y = 0, z = 0.

Прямая в пространстве может быть задана:

1) как линия пересечения двух плоскостей,т.е. системой уравнений:

A₁ x + B₁ y + C₁ z + D₁ = 0, A₂ x + B₂ y + C₂ z + D₂ = 0;

2) двумя своими точками M₁(x₁, y₁, z₁) и M₂(x₂, y₂, z₂), тогда прямая, через них проходящая, задается уравнениями:

= ;

3) точкой M₁(x₁, y₁, z₁), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:

Данное уравнения называются каноническими уравнениями прямой.

Вектор a называется направляющим вектором прямой.

x = x₁ +mt, y = y₁ + nt, z = z₁ + рt.

Решая систему, как систему линейных уравнений относительно неизвестных x и y, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой:

x = mz + a, y = nz + b.

Теперь можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:

.

Билет 27. Поверхности 2-го порядка.

Алгебраическим уравнением 2ой степени наз. уравнение вида Ax²+Bxy+Cy²+Dx+Ey+F=0, где A,B,C,D,E,F - действительные числа. Линии, которые в системе декартовых координат определяются алгебраическим уравнением 2ой степени наз. линиями 2го порядка.

Э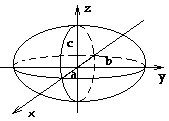 ллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

О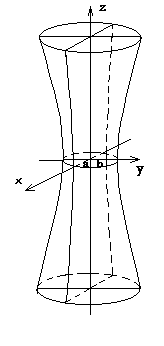 днополосный гиперболоид

Д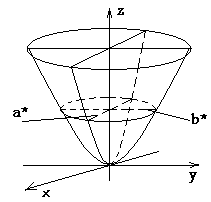 вуполостный гиперболоид

Эллиптический параболоид

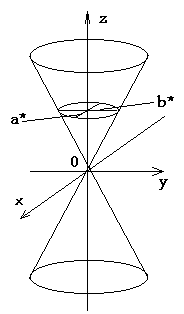
Конус

Билет 28. Действия над комплексными числами.

Итак, всякое комплексное число записывается в виде , где — вещественные числа. При этом предполагается, что:

1. в том и только том случае, если и .

2.

Сложение комплексных чисел.

Суммой комплексных чисел z₁ = a + bi и z₂ = с + di называется комплексное число (a + c) + (b + d)i.

Таким образом:

z₁ + z₂ = (a + bi) + (c + di) = (a + c) + (b + d)i.

Сумма комплексных чисел обладает свойствами:

- коммутативности: z1 + z2 = z2 + z1

- ассоциативности: (z1 + z2) + z3 = z1 + (z2 + z3)

Произведение комплексных чисел.

Произведением комплексных чисел z1 = a + bi и z2 = c + di называется комплексное число (ac - bd)+(ad + bc)i. Определение произведения устанавливается с таким расчетом, чтобы (a + bi) и (c + di) можно было перемножить как алгебраические двучлены, считая при этом, что i*i = -1.

Произведение комплексных чисел обладает свойствами:

коммутативности: z1 * z2 = z2 * z1

ассоциативности: (z1 * z2) * z3 = z1 * (z2 * z3)

дистрибутивности: z1 * (z2 + z3) = z1 * z2 + z1 * z3

На основании определения произведения комплексных чисел можно определить натуральную степень комплексного числа: zⁿ = z * z * ... * z n раз.

Разность комплексных чисел.

Разностью комплексных чисел z1 = a + bi и z2 = c + di называется комплексное число z = z1 - z2 = (a - c) + (b - d)i.

Частное.

Частным от деления комплексного числа z1 на комплексное число z2 называется такое число z, которое удовлетворяет условию z? z2 = z2 ? z= = z1.

Билет 29. Геометрическое изображение комплексных чисел. Модуль и аргумент.

Действительные числа можно изобразить точками прямой линии, как показано на рисунке, где точка A изображает число 4, а точка B число -5. Эти же числа можно изображать также отрезками OA, OB, учитывая не только их длину, но и направление.

Каждая точка M числовой прямой изображает некоторое действительное число (рациональное, если отрезок OM соизмерим с единицей длины, и иррациональное если несоизмерим). Таким образом, на числовой прямой не остается места для комплексных чисел.

Но комплексные числа можно изображать на числовой плоскости. Для этого мы выбираем на плоскости прямоугольную систему координат, с одинаковым масштабом на обеих осях.

Комплексное число a + b·i изображается точкой M, у которой абсцисса x равна абсциссе a комплексного числа, а ордината y равна ординате b комплексного числа.

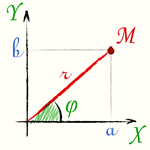
Длина вектора, изображающего комплексное число, называется модулем комплексного числа. Модуль любого комплексного числа, не равного нулю, есть положительное число. Модуль комплексного числа a + b·i обозначается |a + b·i|, а также буквой r. Из чертежа видно, что:

Модуль действительного числа, совпадает с его абсолютным значением. Сопряженные комплексные числа a + b·i и a - b·i имеют один и тотже модуль.

Угол φ между осью абсцисс и вектором OM, изображающим комплексное число a + b·i, называется аргументом комплексного числа a + b·i

Каждое не равное нулю комплексное число имеет бесчисленное множество аргументов, отлючающихся друг от друга на целое число полных оборотов (т.е. на 360°·k, где k - любое целое число). Аргумент комплексного числа связан с его координатами следующими формулами:

Однако ни одна из этих формул в отдельности не позволяет найти аргумент. Для того чтобы найти аргумент комплексного числа, эти формулы надо использовать в совокупности, а также учитывать номер четверти, на координатной плоскости, в которой находится комплексное число.

Билет 30. Тригонометрическая форма комплексного числа. Формула Муавра.

Абсцисса a и ордината b комплексного числа a + b·i выражаются через модуль r и аргумент φ формулами:

1. a = r*cos(φ)

2. b = r*sin(φ)

Поэтому всякое комплексное число можно представить в виде:

a+b*i = r*(cos (φ) + i*sin (φ))

Это так называемая, нормальная тригонометрическая форма, или просто, тригонометрическая форма комплексного числа.

В противоположность тригонометрической форме выражение вида a + b·i называется алгебраической или координатной формой комплексного числа.

Формула Муавра для комплексных чисел , заданная в тригонометрической форме — формула

Формула Муавра сразу следует из формулы Эйлера и правила для экспонент , верного, если b — целое число. (Если b — не целое, то — многозначная функция переменной a и — одно из её значений.)

Открыта французским математиком Абрахамом де Муавро

Билет 31. Корень n-ой степени из комплексного числа.

Корнем n -ой степени из комплексного числа называется такое комплексное число, n-я степень которого равна подкоренному числу.

Из этого определения следует, что из равенства следует равенство .

Из равенства комплексных чисел следует , а аргументы отличаются на число, кратное ; . Отсюда , . Здесь есть арифметическое значение корня, а k – любое целое число. Таким образом, получается формула

.

В этой формуле число k может принимать всевозможные целые значения, но различных значений корня будет только n и они соответствуют значениям k = 0, 1, 2, … , n - 1.

Докажем этот факт. Действительно, правые части в этой формуле различны тогда, когда аргументы и отличаются на величину, не кратную , и будут одинаковыми, если указанные аргументы отличаются на величину, кратную . Поэтому разность не может быть кратна . Из этого результата и следует, что любым подряд взятым n целым числам k соответствуют n различных значений корня.

Пусть теперь k3– целое число, не входящее в эту последовательность подряд взятых значений k . Это число можно представить в виде k3= gn + ki, где g – целое число, а ki – одно из чисел этого ряда, поэтому 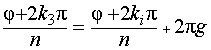, то есть значению k3 соответствует то же значение корня, что и значению ki.

Вывод: корень n -ой степени из комплексного числа имеет n различных значений. Исключением из этого правила является лишь частный случай, когда извлекается корень из нуля. В этом случае все значения корня равны нулю.

Основные определения и задачи линейного программирования.

Задачи оптимального планирования, связанные с отысканием оптимума заданной целевой функции (линейной формы) при наличии ограничений в виде линейных уравнений или линейных неравенств относятся к задачам линейного программирования.

Линейное программирование - наиболее разработанный и широко применяемый раздел математического программирования. Это объясняется следующим:

• математические модели очень большого числа экономических задач линейны относительно искомых переменных;

• эти типы задач в настоящее время наиболее изучены;

• для них разработаны специальные конечные методы, с помощью которых эти задачи решаются, и соответствующие стандартные программы для их решения на ЭВМ;

• многие задачи линейного программирования, будучи решенными, нашли уже сейчас широкое практическое применение в народном хозяйстве;

• некоторые задачи, которые в первоначальной формулировке не являются линейными, после ряда дополнительных ограничений и допущений могут стать линейными или могут быть приведены к такой форме, что их можно решать методами линейного программирования.

Итак, Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.

Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.

Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующих систему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи.

Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального).

В общей постановке задача линейного программирования выглядит следующим образом:

Имеются какие-то переменные х = (х₁ , х₂ , … х_n ) и функция этих переменных f(x) = f (х₁ , х₂ , … х_n ), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G:

В зависимости от вида функции f(x) и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что  а) функция f(x) является линейной функцией переменных х₁ , х₂ , … х_n б) область G определяется системой линейных равенств или неравенств.

Математическая модель любой задачи линейного программирования включает в себя:

• максимум или минимум целевой функции (критерий оптимальности);

• систему ограничений в форме линейных уравнений и неравенств;

• требование неотрицательности переменных.

Или

Задачи.

Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции

(8)

при условиях

(9)

(10)

(11)

где  - заданные постоянные величины и  .

Определение 2.

Функция (8) называется целевой функцией (или линейной формой) задачи (8) – (11), а условия (9) – (11) – ограничениями данной задачи.

Определение 3.

Стандартной (или симметричной} задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (9) и (11), где k = m и l = n.

Определение 4.

Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (10) и (11), где k = 0 и l = п.

Определение 5.

Совокупность чисел  , удовлетворяющих ограничениям задачи (9) – (11), называется допустимым решением (или планом).

Определение 6.

План  , при котором целевая функция задачи (8) принимает свое максимальное (минимальное) значение, называется оптимальным.

Значение целевой функции (8) при плане Х будем обозначать через  . Следовательно, X^*– оптимальный план задачи, если для любого Х выполняется неравенство  [соответственно  ].

Указанные выше три формы задачи линейного программирования эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи. Это означает, что если имеется способ нахождения решения одной из указанных задач, то тем самым может быть определен оптимальный план любой из трех задач.

Чтобы перейти от одной формы записи задачи линейного программирования к другой, нужно уметь, во-первых, сводить задачу минимизации функции к задаче максимизации; во-вторых, переходить от ограничений-неравенств к ограничениям-равенствам и наоборот; в-третьих, заменять переменные, которые не подчинены условию неотрицательности.

В том случае, когда требуется найти минимум функции  , можно перейти к нахождению максимума функции  , поскольку  .

Ограничение-неравенство исходной задачи линейного программирования, имеющее вид “ ”, можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида “ ” – в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство

преобразуется в ограничение-равенство

(12)

а ограничение-неравенство

– в ограничение-равенство

(13)

В то же время каждое уравнение системы ограничений

можно записать в виде неравенств:

(14)

Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.

Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса.

Отметим, наконец, что если переменная  , не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными  и  , приняв  .

Билет 33. Графический метод решения задач линейного программирования.

Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно.

Пусть задача линейного программирования задана в двумерном пространстве, то есть ограничения содержат две переменные. Найти минимальное значение функции

При

Допустим, что система (2) при условии (3) совместна и её многоугольник решений ограничен. Каждое из неравенств (2) и (3), как отмечалось выше, определяет полуплоскость с граничными прямыми:

. Линейная функция (1) при фиксированных значениях является уравнением прямой линии: . Построим многоугольник решений системы ограничений (2) и график линейной функции (1) при . Тогда поставленной задаче линейного программирования можно дать следующую интерпретацию. Найти точку многоугольника решений, в которой прямая опорная и функция при этом достигает минимума.

Значения возрастают в направлении вектора , поэтому прямую передвигаем параллельно самой себе в направлении вектора . Прямая дважды становится опорной по отношению к многоугольнику решений (в точках и ), причем минимальное значение принимает в точке . Координаты точки находим, решая систему уравнений прямых и .

Алгоритм графического метода решения задач линейного программирования с двумя переменными:

1. Построить область допустимых решений.

2. Если область допустимых решений является пустым множеством, то задача не имеет решения ввиду несовместно­сти системы ограничений.

3. Если область допустимых решений является непустым множеством, построить нормаль линий уровня n = (c₁ ,c₂) и одну из линий уровня, имеющую общие точки с этой областью.

4. Линию уровня переместить до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум - в противоположном направлении.

5. Если при перемещении линии уровня по области допус­тимых решений в направлении, соответствующем приближе­нию к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения ввиду неограни­ченности целевой функции.

6. Если задача линейного программирования имеет опти­мальное решение, то для его нахождения нужно решить сис­тему уравнений для прямых, ограничивающих область допус­тимых решений и имеющих общие точки с соответствующей опорной прямой. Если целевая функция задачи достигает мак­симума (минимума) в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек.

Билет 34. Статистическое классическое геометрическое определение вероятности.

Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике же весьма часто встречаются испытания, число возможных исходов которых бесконечно. В таких случаях классическое определение неприменимо. Уже это обстоятельство указывает на ограниченность классического определения.

Наиболее слабая сторона классического определения состоит в том, что очень часто невозможно представить результат испытания в виде совокупности элементарных событий. Еще труднее указать основания, позволяющие считать элементарные события равновозможными. Обычно о равновозможности элементарных исходов испытания говорят из соображений симметрии. Так, например, предполагают, что игральная кость имеет форму правильного многогранника (куба) и изготовлена из однородного материала. Однако задачи, в которых можно исходить из соображений симметрии, на практике встречаются весьма редко. По этой причине наряду с классическим определением вероятности используют и другие определения, в частности статистическое определение: в качестве статистической вероятности события принимают относительную частоту или число, близкое к ней. Например, если в результате достаточно большого числа испытаний оказалось, что относительная частота весьма близка к числу 0,4, то это число можно принять за статистическую вероятность события.

Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности — вероятности попадания точки в область (отрезок, часть плоскости и т. д.).

Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством

Р = Длина l / Длина L.

Билет 35. Вероятность сложных событий. Теорема сложения и умножения вероятностей.

Сложные события представляют собой серию опытов и комбинацию всех возможных исходов. Очень важно учесть все возможные исходы, для чего составляется «дерево вероятностей», на котором отражаются последовательность экспериментов и их результаты.

Дерево вероятностей

Опыты представлены здесь последовательностью кружков, а каждый исход — «ветвью» (линией) от соответствующего кружка. Вероятность соответствующего исхода указана около «ветви», а вероятность всего сложного события в ее конце.

Правило сложения вероятностей

Для простоты рассмотрим лишь два события — А и В. Правило сложения вероятностей применяется для подсчета вероятности осуществления событий А или В, или их обоих сразу:

Р(А + В) = Р(А) + А(В) - Р(АВ).

Если события А и В несовместимы, то:

Р(А+В) = Р(А) + Р(В).

Так как события А и В — несовместимые, то они не могут произойти одновременно, значит:

Р(АВ) = 0.

Правило умножения вероятностей

Это правило применяется, когда требуется найти вероятность того, что события А и В произойдут одновременно. Правило умножения вероятностей состоит в следующем:

Р (АВ ) = Р (А ) х Р (В/А ).

Если А и В независимы, то Р (В/А) = Р (В), и правило выглядит так:

Р (АВ ) = Р (А ) х Р (В ).

Билет 36. Формула полной вероятности и формула Байеса.

Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.

Если событие А может произойти только при выполнении одного из событий , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле

Эта формула называется формулой полной вероятности.

Вновь рассмотрим полную группу несовместных событий , вероятности появления которых . Событие А может произойти только вместе с каким-либо из событий , которые будем называть гипотезами. Тогда по формуле полной вероятности

Если событие А произошло, то это может изменить вероятности гипотез .

По теореме умножения вероятностей:

Откуда:

Аналогично для остальных гипотез:

Полученная формула называется формулой Байеса.

Билет 37. Формула Бернулли и формула Пуассона.

Формула Бернулли определяет вероятность появления ровно m раз события А в серии из n независимых испытаний, в каждом из которых P(A)=p, q=1-p - вероятность противоположного события, и имеет вид:

Pn(m)=C(сверху m снизу n)*p^m*q^(n-m).

Вероятность появления события А:

1)менее m раз P(X<m)=Pn(0)+Pn(1)+..+Pn(m-1)

2)более m раз P(X>m)=Pn(m+1)+Pn(m+2)+..+Pn(n)

3)не менее m раз P(X≥m)=Pn(m)+Pn(m+1)+..+Pn(n)

4)не более m раз P(X≤m)=Pn(0)+Pn(1)+..+Pn(m)

При больших n и маленьких р используется формула Пуассона:

Pn(m)=(λ^m/m!)*e^(-λ), где λ = np.

Билет 38. Отображения и функции. Типы отображений.

Отображением множества E в множество F, или функцией, определенной на E со значениями в F, называется правило, или закон f, который каждому элементу ставит в соответствие определенный элемент .

Отображение (функцию) обычно обозначают буквой f или символом , указывая тем самым, что f отображает множество E в F. Употребляется также обозначение , указывающее, что элементу x соответствует элемент f(x). Иногда функцию удобно задавать посредством равенства, в котором содержится закон соответствия. Например, можно говорить, что "функция f определена равенством

= ". Если "y" - общее наименование элементов множества F, т. е. F = {y}, то отображение записывают в виде равенства y = f(x) и говорят, что это отображение задано явно.

Типы

отображений: Отображения на-ся

сюръективными («на»), если f(A)=B, т.е.

каждый Эл. мн-ва B явл образом хотя б 1

эл мн-ва А Инъективным мн-вом, если

различаются: x1¹x2Þf(x1)¹f(x2).

Биекция, если оно одновременно

сюръективно и инъективно.

Предел последовательности. Геометрический смысл предела.

Пусть каждому  по некоторому закону поставлено в соответствие действительное число x_n. Тогда говорят, что определена последовательность чисел x₁,x₂,…,x_n  или {x_n}.

         Число x_n –элемент последовательности.

 

Пример 17.2.

1)  ;

         2)  .

 

Если x_n=const, то последовательность называется постоянной.

 

Последовательность {x_n} ограничена, если  .

 

Определение 17.3.

Число а называется пределом числовой последовательности {x_n}, если для любого положительного числа  ε существует номер N такой,  что при всех n>N  выполняется неравенство  .

 

Обозначение:   или  .

Последовательность, имеющая предел называется сходящейся, не имеющая его – расходящейся.

 

Пример 17.3.

Определить предел последовательности  .

(Ответ:  .)