64 Вопрос. Частные производные и дифференциалы высших порядков. Матрица Гессе.

Если функция , определенная в некоторой области , имеет частную производную по переменной , то эта частная производная вновь является некоторой функцией, которая в свою очередь может иметь частную производную . Эта функция называется второй производной функции по переменным и обозначается символом . Аналогичным образом определяются частные производные .

Мы определили частные производные второго порядка. Третьи частные производные есть производные по соответствующим переменным от вторых производных. Вторые или третьи частные производные часто обозначаются следующим образом: и так далее.

Возникает вопрос о том, влияет ли порядок дифференцирования на вычисленную частную производную. В общем случае влияет, но если функция удовлетворяет некоторым условиям, то нет. Сформулируем соответствующую теорему для случая функции двух переменных.

Теорема (Шварца). Если функция непрерывна вместе со своими вторыми частными производными в некоторой окрестности , точки , то

.

Дифференциалы высших порядков.

Пусть в области задана некоторая функция , имеющая непрерывные частные производные первого порядка. Тогда она будет дифференцируема в этой области, и ее дифференциал имеет вид

,

где - произвольные приращения независимых переменных .

Видим, что также является функцией от . Если существуют непрерывные частные производные второго порядка функции для , то можно говорить о дифференциале от первого дифференциала , который называется дифференциалом второго порядка от и обозначается символом .

Приращения при этом рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему.

Запишем формулу второго дифференциала для функции двух переменных :

.

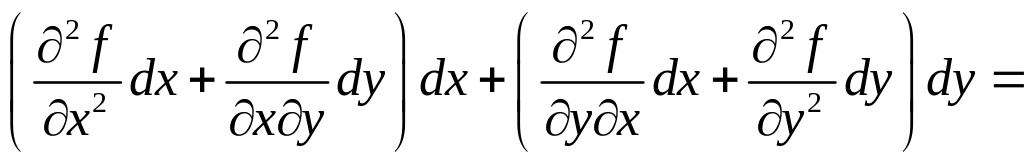
Если первый дифференциал символически записать следующим образом

,

то второй будет иметь вид

.

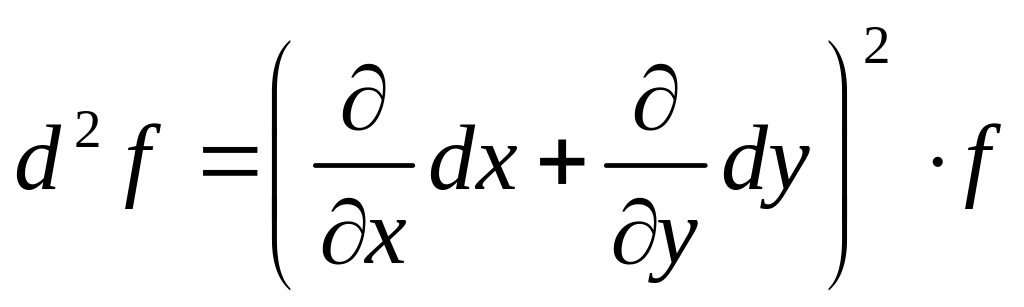Можно показать, что аналогичная формула справедлива для дифференциалов любого порядка:

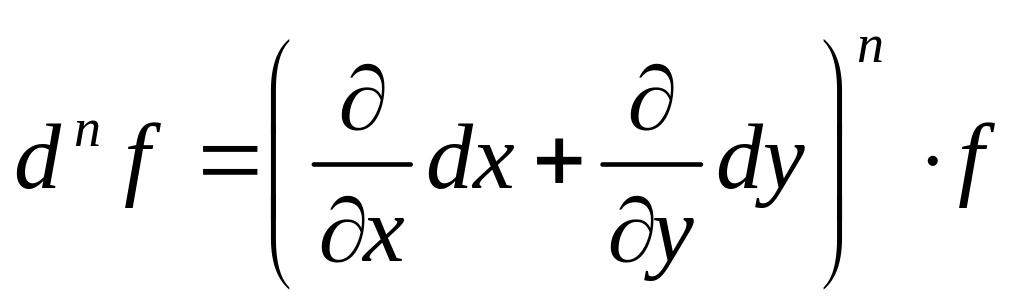
Формула Тейлора.

Теорема. Если функция определена и непрерывна вместе со своими частными производными до порядка включительно в некоторой окрестности точки , то для приращения справедлива формула

.

Матрица Гессе.

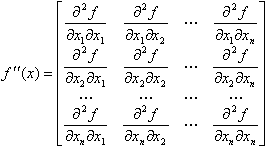
Билет 65. Экстремум функции двух переменных.

Функция имеет максимум (минимум) в точке , если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке некоторой окрестности точки , то есть (соответственно ) для всех точек , принадлежащих этой окрестности. Максимум и минимум функции называется ее экстремумом. Точка , в которой функция имеет экстремум, называется точкой экстремума.

Необходимое условие экстремума: если дифференцируемая функция достигает экстремума в точке , то ее частные производные первого порядка в этой точке равны нулю, то есть: , .

Точки, в которых частные производные равны нулю, называются стационарными точками. Стационарные точки и точки, в которых производные не существуют и которые лежат внутри области определения функции, называются критическими точками. Не всякая критическая точка является точкой экстремума.

Пусть стационарная точка функции . Обозначим , , и составим дискриминант . Тогда:

если , то функция имеет в точке экстремум, а именно минимум, при (или ) и максимум, при (или );

если , то в точке экстремума нет;

если , то требуется дальнейшее исследование (сомнительный случай).