66 Экстремум функции нескольких переменных
О:
Точка
называется
точкой максимума (минимума)
функции
(х,
у), если
Максимумы и минимумы функции называются ее экстремумами (рис. 12.1).
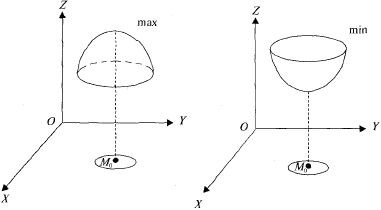
Рис. 12.1
Примеры:
1)
Очевидно т. (1, 2) является т. mm, так как все остальные значения х и у дадут z > -1
2)
В
данном случае т.
(0,
0) является т. max, так как
Т: (необходимое условие экстремума)
Если
функция г =
(х,у)
имеет экстремум в т.
то
или
обращаются в нуль, или не существуют
Пусть
у =
тогда
—
функция одной переменной. Так как при
х =
она
имеет экстремум, то
Доказательство
при х =
аналогично
Эти условия не являются достаточными.
Пример:
обращаются
в нуль в т. О(0,0),
но ху > 0 при х > 0, у > 0, ху < 0 при х < 0, у > 0, т.е. определение экстремума не выполняется.
Приведем достаточные условия экстремума для стационарных
т.
в
которых
Т:
(достаточные условия экстремума) Пусть
в некоторой области, содержащей
т.
функция
имеет
непрерывные частные производные до
третьего порядка включительно и эта
точка является стационарной.
Пусть
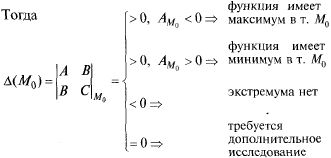
Доказательство см. в [11. С. 419].
Пример:
Исследовать на экстремум
—
стационарные
точки,
1)
—
точка минимума,
2)т.
—
точка
максимума,
3)
экстремума
нет,
4)
экстремума
нет
Для
функции п переменных
определение
экстремума и
необходимые
условия сохраняются. Необходимое условие
в случае дифференцируемой функции
кратко
запишется в виде:
Сформулируем достаточные условия экстремума.
Т:
Если в стационарной т.
второй
дифферен-
циал
является
положительно (отрицательно) определенной
квадратичной формой, то
—
точка min (max)
Доказательство см. в [11. С. 424].
Сформулированные
ранее достаточные условия экстремума
для функции
являются
следствием данной теоремы.
Билет 67. Условный экстремум. Метод множителей Лагранжа
Пусть рассматривается функция z = f(x,y), аргументы х и у которой удовлетворяют условию g (x,y) = С, называемому уравнением связи.
Определение. Точка (х0, у0) называется точкой условного максимума (минимума), если существует такая окрестность этой точки, что для всех точек (х,у) из этой окрестности удовлетворяющих условию g (x,y) — С, выполняется неравенство
f(xo, yo) ≥f(x,y) (fxо, уо) ≤f(х,у)
Наиболее простым способом нахождения условного экстремума функции двух переменных является сведение задачи к отысканию экстремума функции одной переменной. Допустим уравнение связи g(x,y) = С удалось разрешить относительно одной из переменных, например, выразить у через х: у = φ>(х). Подставив полученное выражение в функцию двух переменных, получим z = f(x,y) = f(x, φ(х)), т.е. функцию одной переменной. Ее экстремум и будет условным экстремумом функции z=f(x,y).
Для отыскания условного экстремума в общем случае используется метод множителей Лагранжа.
Рассмотрим функцию трех переменных L(х, у, λ) = f(х, у) +x[g(x,y) – C].
Эта функция называется функцией Лагранжа, а λ — множителем Лагранжа. Верна следующая теорема.
Теорема. Если точка (x0 , у0) является точкой условного экстремума функции z =f(х,у) при условии g (х,у) = С, то существует значение λ0 такое, что точка (x0, у0, λ 0) является точкой экстремума функции L(х,у, λ).
Таким образом, для нахождения условного экстремума функции z = f (х,у) при условии g(x,y) = С требуется найти решение системы
L`x=f `x(х,у)+λg'х(х,у) = 0,
L`y=f `y(x,y)+λ g'y(x,y)=0,
L'λ=g(x,y)-C=0.
Последнее из этих уравнений совпадает с уравнением связи. Первые два уравнения системы можно переписать в виде gradf = -X grad g,
т.е. в точке условного экстремума градиенты функций f (x,y) и g(x,y) коллинеарны.
В случае, если число переменных более двух, может рассматриваться и несколько уравнений связи. Соответственно в этом случае будет и несколько множителей Лагранжа.
Мы не рассматриваем здесь достаточные условия условного экстремума. Отметим только, что во многих задачах критическая точка функции Лагранжа оказывается единственной и соответствует не только локальному, но и глобальному условному минимуму или максимуму.
68. Функции полезности. Кривые безразличия.
Функция полезности (функция предпочтений) – в широком смысле зависимость полезности, т. е. результата, эффекта некоторого действия от уровня (интенсивности) этого действия.
Изучая в теории потребительского спроса кривые безразличия (линии, вдоль которых полезность двух благ х и у одна и та же), например задаваемые в виде ху=U и линию бюджетного ограничения рхх+руу=I при ценах благ рх и ру и доходе потребителя I, мы можем установить оптимальные количества благ х0 и у0, имеющих максимальную полезность U0.
Линии уровня функции полезности (кривые безразличия) позволяют рассматривать вопросы замещения одного товара другим и иллюстрировать решение задачи об оптимальном потреблении (потребительского выбора).
Оптимальное потребление обеспечивается значением (х0, у0) – координатами точки касания кривой безразличия и линии уровня затрат. В этой точке заданная полезность достигается наиболее экономичным образом.
Другой пример кривых безразличия возникает в теории инвестиций.
Портфель ценных бумаг (под портфелем понимается совокупность определенных ценных бумаг в определенных количествах) характеризуется двумя основными параметрами – ожидаемой доходностью r и риском σ. Каждому портфелю можно поставить в соответствие точку на координатной плоскости (σ, r), и тогда множество всех возможных портфелей представляет некоторую область D.
Очевидно, что при равных доходностях инвестор предпочтет портфель с меньшим риском. Т. о., кривые безразличия – линии уровня функции предпочтения U=U(σ, r) – выпуклы вниз. Точка Т, в которой линия безразличия касается области D, соответствует наиболее предпочтительному для данного инвестора портфелю. Эта теория в 1952 г. была предложена америк. экономистом Харри Марковицем.
68. Функции полезности. Кривые безразличия.
Функция полезности (функция предпочтений) – в широком смысле зависимость полезности, т. е. результата, эффекта некоторого действия от уровня (интенсивности) этого действия.
Изучая в теории потребительского спроса кривые безразличия (линии, вдоль которых полезность двух благ х и у одна и та же), например задаваемые в виде ху=U и линию бюджетного ограничения рхх+руу=I при ценах благ рх и ру и доходе потребителя I, мы можем установить оптимальные количества благ х0 и у0, имеющих максимальную полезность U0.
Линии уровня функции полезности (кривые безразличия) позволяют рассматривать вопросы замещения одного товара другим и иллюстрировать решение задачи об оптимальном потреблении (потребительского выбора).
Оптимальное потребление обеспечивается значением (х0, у0) – координатами точки касания кривой безразличия и линии уровня затрат. В этой точке заданная полезность достигается наиболее экономичным образом.
Другой пример кривых безразличия возникает в теории инвестиций.
Портфель ценных бумаг (под портфелем понимается совокупность определенных ценных бумаг в определенных количествах) характеризуется двумя основными параметрами – ожидаемой доходностью r и риском σ. Каждому портфелю можно поставить в соответствие точку на координатной плоскости (σ, r), и тогда множество всех возможных портфелей представляет некоторую область D.
Очевидно, что при равных доходностях инвестор предпочтет портфель с меньшим риском. Т. о., кривые безразличия – линии уровня функции предпочтения U=U(σ, r) – выпуклы вниз. Точка Т, в которой линия безразличия касается области D, соответствует наиболее предпочтительному для данного инвестора портфелю. Эта теория в 1952 г. была предложена америк. экономистом Харри Марковицем.
Билет 69. Метод наименьших квадратов.
Согласно наиболее распространенному и теоретически обоснованному методу наименьших квадратов в качестве неизвестных параметров функции f(x) выбирают такие значения, чтобы сумма квадратов невязок δi , или отклонений "теоретических" значений f(xi), найденных по эмпирической формуле y=f(x), от соответствующих опытных значений уi, т.е. была минимальной.
Пусть в качестве функции у = f(х) взята линейная функция y=ax+b, и задача сводится к отысканию таких значений параметров а и Ь, при которых функция принимает наименьшее значение. Заметим, что функция S=S(a; b) есть функция двух переменных а и b до тех пор, пока мы не нашли, а затем зафиксировали их "наилучшие" (в смысле метода наименьших квадратов) значения, а хi , уi, — постоянные числа, найденные экспериментально.