
- •9. Вырожденные и невырожденные матрицы. Ранг матрицы. Теорема о ранге матрицы.
- •Уравнение плоскости по трем точкам:
- •4. Уравнение плоскости по точке и двум неколлинеарным векторам
- •Геометрический смысл предела числовой последовательности
- •Основные свойства сходящихся последовательностей
- •Арифметические действия над последовательностями, имеющими предел
- •1. Бесконечно малые функции при х
- •2. Предел функции при х и его свойства.
- •1. Бесконечно малые функции при х а
- •2. Предел функции в точке
- •3. Односторонние пределы
- •44 Вопрос. Глобальные свойства непрерывных функций.
- •Формула конечных приращений
- •Понятие дифференциала
- •Свойства дифференциала. Инвариантность формы дифференциала
- •51Производные основных элементарных функций
- •53 Вопрос. Логарифмическая производная. Производная функции u(X)V(X).
- •56 Вопрос. Направление вогнутости. Точки перегиба.
- •64 Вопрос. Частные производные и дифференциалы высших порядков. Матрица Гессе.
- •66 Экстремум функции нескольких переменных
- •Билет 70. Неопределенный интеграл. Простейшие свойства.
- •Для неопределённого интеграла
- •Для определённого
- •Метод замены переменной (метод подстановки)
- •72Интегрирование дробно-рациональных функций
Билет 1. Множества. Основные понятия. Операции над мн-вами. Декартово произведение множеств.
Множество и элемент множества относятся к числу первичных понятий, для которых не существует определений в строгом смысле слова. Поэтому обычно говорят о множестве как о наборе предметов ( элементов множества ), наделённых определёнными общими свойствами. Множество книг в библиотеке, множество автомобилей на стоянке, множество звёзд на небосводе, растительный и животный мир Земли – всё это примеры множеств.
Над множествами определены следующие операции:
-
объединение (или сумма) (обозначается
как
![]() );
);
-
разность (обозначается как
![]() реже
реже
![]() );
);
-
дополнение (обозначается как
![]() или
или
![]() );
);
-
пересечение (или произведение)
(обозначается как
![]() );
);
-
симметрическая разность (обозначается
как
![]() реже
реже
![]() ).
).
ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ — множество А × В всех упорядоченных пар элементов (a, b), из которых a принадлежит множеству A, b — множеству B. Порядок следования пар может быть любым, но расположение элементов в каждой паре (векторе, кортеже) определяется порядком следования перемножаемых элементов. Поэтому A × B ≠ B × A, если B ≠ A.
Если обобщить сказанное на любое количество множеств A1, A2, ..., An, то Д. п. записывается так:

Если перемножаются одинаковые множества, используется обозначение степени: An = A × A × A ×...× А при n сомножителях.
2 Линейное пространство. Основные понятия.Аксиомы.
Пусть ![]()
![]() множество
элементов произвольной природы, для
которых определены операции сложения
и умножения на действительное число:
множество
элементов произвольной природы, для
которых определены операции сложения
и умножения на действительное число:
паре
элементов множества ![]() ,
, ![]() отвечает
элемент
отвечает
элемент ![]() ,
называемый суммой
,
называемый суммой ![]() и
и ![]() ;
;
паре
, ![]() отвечает
элемент
отвечает
элемент ![]() ,
называемый произведением числа
,
называемый произведением числа ![]() и
элемента
.
и
элемента
.
Будем
называть множество
линейным
пространством,
если для всех его элементов определены
операции сложения и умножения на
действительное число и для любых
элементов ![]() и
произвольных чисел
и
произвольных чисел ![]() справедливо:
справедливо:
 ,
сложение коммутативно;
,
сложение коммутативно;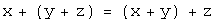 ,
сложение ассоциативно;
,
сложение ассоциативно;существует единственный нулевой элемент
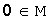 такой,
что
такой,
что 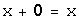 ,
, 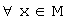 ;
;для каждого элемента существует единственный противоположный элемент
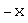 такой,
что
такой,
что  ,
,
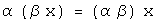 ,
умножение на число ассоциативно;
,
умножение на число ассоциативно;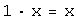 ,
;
,
; ,
умножение на число дистрибутивно
относительно сложения элементов;
,
умножение на число дистрибутивно
относительно сложения элементов;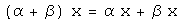 ,
умножение вектора на число дистрибутивно
относительно сложения чисел.
,
умножение вектора на число дистрибутивно
относительно сложения чисел.
Равенства 1--8 называют аксиомами линейного пространства.
Линейное пространство часто называют векторным пространством, а его элементы -- векторами.
Базис и размерность линейного пространства. Координаты вектора в заданном базисе
Говорят,
что элемент (вектор)
линейного
пространства ![]() линейно
выражается через
элементы (векторы)
линейно
выражается через
элементы (векторы) ![]() ,
если его можно представить в виде линейной
комбинацииэтих
элементов, т.е. представить в виде
,
если его можно представить в виде линейной
комбинацииэтих
элементов, т.е. представить в виде ![]() .
.
Если
любой вектор системы ![]() векторов
линейного пространства
линейно
выражается через остальные векторы
системы, то система векторов
называется линейно
зависимой.
векторов
линейного пространства
линейно
выражается через остальные векторы
системы, то система векторов
называется линейно
зависимой.
Система векторов, которая не является линейно зависимой, называется линейно независимой.
Справедливо следующее утверждение.
Система
векторов
линейного пространства
линейно
независима тогда и только тогда, когда
из равенства ![]() следует
равенство нулю всех коэффициентов
следует
равенство нулю всех коэффициентов ![]() .
.
Если
в линейном пространстве
существует
линейно независимая система из ![]() векторов,
а любая система из
векторов,
а любая система из ![]() -го
вектора линейно зависима, то
число
называется размерностью
пространства
и
обозначается
-го
вектора линейно зависима, то
число
называется размерностью
пространства
и
обозначается ![]() .
В этом случае пространство
называют
.
В этом случае пространство
называют ![]() -мерным
линейным пространством или
-мерным
векторным пространством.
-мерным
линейным пространством или
-мерным
векторным пространством.
Любая
упорядоченная линейно независимая
система
векторов ![]() линейного
пространства
образует базис
пространства и
любой вектор
линейного
пространства
образует базис
пространства и
любой вектор ![]() единственным
образом выражается через векторы
базиса:
единственным
образом выражается через векторы
базиса: ![]() .
.
Числа ![]() называют координатами
вектора
в
базисе
и
обозначают
называют координатами
вектора
в
базисе
и
обозначают ![]() .
При этом для любых двух произвольных
векторов
-мерного
линейного пространства
,
.
При этом для любых двух произвольных
векторов
-мерного
линейного пространства
, ![]() и
произвольного числа
справедливо:
и
произвольного числа
справедливо: ![]() и
и ![]() .
.
Это
означает, что все
-мерные
линейные пространства “устроены”
одинаково -- как пространство ![]() векторов-столбцов
из
действительных
чисел, т.е. что все они изоморфны
пространству
.
векторов-столбцов
из
действительных
чисел, т.е. что все они изоморфны
пространству
.
Линейные
пространства ![]() и
и ![]() называются изоморфными,
если между их элементами можно установить
такое взаимно однозначное соответствие,
что если векторам
и
называются изоморфными,
если между их элементами можно установить
такое взаимно однозначное соответствие,
что если векторам
и ![]() из
соответствуют
векторы
и
из
соответствуют
векторы
и ![]() из
,
то вектору
из
,
то вектору ![]() соответствует
вектор
соответствует
вектор ![]() и
при любом
вектору
и
при любом
вектору ![]() соответствует
вектор
соответствует
вектор ![]() .
.
Изоморфизм -мерных линейных пространств пространству означает, что соотношения между элементами -мерного линейного пространства и операции с ними можно изучать как соотношения между векторами из и операции с ними и что всякое утверждение относительно векторов из справедливо для соответствующих элементов любого -мерного линейного пространства.
Например, доказано, что система векторов из
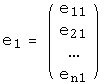 ,
, 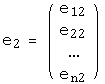 ,...,
,..., 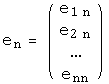
образует базис в тогда и только тогда, когда отличен от нуля определитель матрицы, со столбцами :

Для векторов из это означает, что они образуют базис в тогда и только тогда, когда отличен от нуля определитель матрицы, столбцами которой являются компоненты векторов .
Пусть
и ![]() --
два базиса в
. Матрицей
перехода от
базиса
к
базису
называется
матрица
--
два базиса в
. Матрицей
перехода от
базиса
к
базису
называется
матрица ![]() ,
столбцами которой являются координаты
векторов
в
базисе
:
,
столбцами которой являются координаты
векторов
в
базисе
:
|
|
|
|
... |
... |
|
|
![]()
 ,
, ![]()
Вектор
линейно
выражается через векторы обоих базисов.
Тогда, если ![]() ,
то координаты вектора
в
базисе
,
и его координаты в базисе
связаны
соотношениями
,
то координаты вектора
в
базисе
,
и его координаты в базисе
связаны
соотношениями

3Билет Пространство R*n. Экономическая
интерпретация (пространство благ и
товаров). Упорядоченная совокупность n вещественных
чисел наз n-мерным арифвектором а числа
координатами Мн-во всех n-мерных векторов на
котором введены операции сложения и умножения на
числа наз-ся n-мерным векторным пространством.
(R*n), экономическая интерпретация благ и товаров.
Товар-определённое благо или услуга, поступившая в
продажу в определённом месте и в опред время.
Предположим что сущ-ет конечное число товаров n;
кол-во каждого из них хар-ся набором товаров
x=(x1.x2...xn) Тк может б куплено любое неотркол-во
любого товара то все наборы явл-ся векторами прост-ва
товаров Тогда обозначая ч/з х и Т кол-во I-того товара,
мы получаем пространство благ и товаров:
T=x1,x2…xn/ xi0, i=1.n2) если истолков как точки:
Н-р (а,b) задает вектор и точку. Любая упоряд пара
чисел: арифметич точка, а числа a1…an координаты
точка (000) начало коор-т. Обозначение точек ч\з
большие буквы. Пусть A и B точки. Вектор AB ариф-й
вектор. Мнво всех ариф точек с n корд в кот двум
точкам сопоставлен вектор ABR*n n-МЕРНОЕ
АРИФ ТОЧЕЧНОЕ ПР-ВО А*n Мн-во ВЫПУКЛО если
вместе с любыми двумя точками оно содержит весь
отрезок. ПОЛУПР-ВО-мн-во точек X=(x1,x2///) корд
кот удовл-ют заданному линейному нер-ву: a1x1+a2x2+…+b СКАЛЯР ПРОИЗ-Е-число
=сумме произв-ий одноименных компонентов этих
векторов xy=x1y1+x2y2+… ДЛИНА-выражение
||x||=корень из x1*2+x2*2… Если k1,k2… вещ числа,
а1,а2…n-мерные векторы то b=k1a1+k2a2+… -линейная
комбин Сис-ма векторов ЛИНЕЙНО ЗАВИС, если есть
лямда…нерво1а1+2ф2…=0 Сис-ма векторов из
Rn –базис прост-ва если:-векторы линейно независ. –
любой вектор из Rn явл линейной комбин ывекторов
данной сис
4 Билет 4. Переход к новому базису.
Пусть
в пространстве
![]() имеется два базиса:
имеется два базиса:
![]() и
и
![]() .
.
Первый условимся называть старым базисом, второй – новым. Каждый из векторов нового базиса, по Теореме, можно линейно выразить через векторы старого базиса:
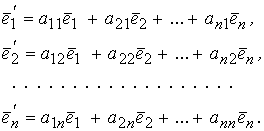
Новые базисные векторы получаются из старых с помощью матрицы

При этом коэффициенты их разложений по старым базисным векторам образуют столбцы этой матрицы. Матрица А называется матрицей перехода от базиса к базису .
Определитель матрицы А не равен нулю, так как в противном случае ее столбцы, а следовательно и векторы , были бы линейно зависимы.
Обратно,
если
![]() ,
то столбцы матрицы линейно независимы,
и следовательно векторы
,
получающиеся из базисных векторов
с помощью матрицы А, линейно независимы
и значит образуют некоторый базис. Таким
образом, матрицей перехода может служить
любая квадратная матрица порядка n
с отличным от нуля определителем.
,
то столбцы матрицы линейно независимы,
и следовательно векторы
,
получающиеся из базисных векторов
с помощью матрицы А, линейно независимы
и значит образуют некоторый базис. Таким
образом, матрицей перехода может служить
любая квадратная матрица порядка n
с отличным от нуля определителем.
Рассмотрим
теперь, как связаны между собой координаты
одного и того же вектора в старом и новом
базисах. Пусть
![]() в старом базисе и
в старом базисе и
![]() - в новом. Подставляя в последнее равенство
вместо
их выражение , получим, что
- в новом. Подставляя в последнее равенство
вместо
их выражение , получим, что
 Таким образом,
старые координаты вектора
Таким образом,
старые координаты вектора
![]() получатся из новых его координат с
помощью той же матрицы А, только
коэффициенты соответствующих разложений
образуют строки этой матрицы.
получатся из новых его координат с
помощью той же матрицы А, только
коэффициенты соответствующих разложений
образуют строки этой матрицы.
Билет 5. Евклидово пространство. Норма вектора в евклидовом пространстве.
Евклидово
пространство - пространство, свойства
которого описываются аксиомами евклидовой
геометрии. В более общем смысле Е. п.
называется n-мepное векторное пространство,
в котором возможно ввести некоторые
специальные координаты (декартовы) так,
что метрика его будет определена
следующим образом: если точка М имеет
координаты (х1, х2,..., xn), а точка М* —
координаты (x1*, x2*,..., xn*), то расстояние
между этими точками
![]()
Нормой
вектора
в
![]() назовем корень квадратный из его
скалярного квадрата
назовем корень квадратный из его
скалярного квадрата
![]()
Векторы
и
![]() ,
для которых
,
для которых
![]() ,
назовем ортогональными. В этом случае
будем писать
,
назовем ортогональными. В этом случае
будем писать
![]() .
.
В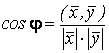 евклидовом пространстве
угол
евклидовом пространстве
угол
![]() между ненулевыми векторами
и
будем определять по формуле
между ненулевыми векторами
и
будем определять по формуле
Легко
видеть, что в силу неравенства
Коши-Буняковского
![]() .
.
Билет 6. Матрицы, действия с матрицами
Матрица – это совокупность mn чисел, расположенных в виде прямоугольной таблицы, где m строк и n столбцов.
Матрица размера mn, где элемент = 0 - нулевая матрица.
Матрицы обычно обозначают прописными латинскими буквами А, В, С…
Когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».
Если в матрице один столбец или одна строка , то такие матрицы называют векторами.
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной.
Действия с матрицами:
Вынесение минуса из матрицы (внесение минуса в матрицу).
Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:
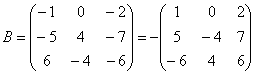 .
Внесение минуса производится аналогично!
.
Внесение минуса производится аналогично!
2Умножение матрицы на число.
3Транспонирование матрицы.
Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.
Т ранспонированная
матрица обычно обозначается надстрочным
индексом или штрихом справа вверху.
ранспонированная
матрица обычно обозначается надстрочным
индексом или штрихом справа вверху.
4 Сумма (разность) матриц.
5Умножение матриц.
6Нахождение обратной матрицы.
7 билет. Определители. Свойства определителей.
Понятие определителя водится только для квадратной матрицы.
Определителем n-го порядка квадратной матрицы называется число, равное алгебраической сумме n!слагаемых, каждое из которых представляет собой произведение n элементов матрицы А, взятых из разных строк и разных столбцов со знаком «+» («-»), если подстановка, составленная из индексов сомножителей чётная( нечётная).
Свойства:
1. определители не меняются при транспонировании.
2. если одна из строк определителя состоит из нулей, то определитель равен нулю
3. если в определители переставить две строки, то определитель меняет знак
4. определитель, содержащий две одинаковые строки, равен нулю
5. если все элементы некоторой строки определителя умножить на некоторое число К, то сам определитель умножится на К.
6. определитель, содержащий две пропорциональные строки, равен нулю
7. если все элементы i-й строки определителя n-го порядка представлены в виде суммы двух слагаемых: aij= bj+cj (j= 1,n),- то определитель равен сумме двух определителей, у которых все строки, кроме i-й,- такие же, как и в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в других- из элементов cj
8. определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженных на одно и то же число
Билет 8. Миноры и алгебраические дополнения элементов матрицы. Разложение определителя по строке или столбцу.
Минором Mi j элемента ai j определителя d n-го порядка называется определитель порядка n-1, который получается из d вычеркиванием строки и столбца, содержащих данный элемент.
Алгебраическим дополнением элемента ai j определителя d называется его минор Mi j, взятый со знаком (-1) i + j. Алгебраическое дополнение элемента ai j будем обозначать Ai j. Таким образом, Ai j = (-1) i + j Mi j.
Способы практического вычисления определителей, основанные на том, что определитель порядка n может быть выражен через определители более низких порядков, дает следующая теорема.
Теорема (разложение определителя по строке или столбцу).
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки
d = ai
1
Ai
1
+ ai
2
Ai
2
+... + ai
n
Ai
n
(i =
![]() )
)
или j- го столбца
d = a1 j A1 j + a2 j A2 j +... + an j An j (j = ).
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.

9. Вырожденные и невырожденные матрицы. Ранг матрицы. Теорема о ранге матрицы.
Матрица называется вырожденной, если ее определитель равен нулю, и невырожденной, если определитель матрицы отличен от нуля.
Пример:
![]()
![]()
Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка.
Теорема о ранге матрицы: ранг матрицы = макс числу ее линейно независимых строк или столбцов, через кот линейно выражаются все ост ее строки(столбцы)
Доказательство.
Рассмотрим образ отображения
![]() . Образ состоит из всевозможных линейных
комбинаций строк матрицы А, следовательно,
размерность образа равна строчному
рангу матрицы А.
. Образ состоит из всевозможных линейных
комбинаций строк матрицы А, следовательно,
размерность образа равна строчному
рангу матрицы А.
Из
представления
![]() ,
следует, что ядро
,
следует, что ядро
![]() имеет размерность равную (n – столбцовый
ранг), значит, размерность образа равна
n-(n-столбцовый ранг) = столбцовый ранг.
имеет размерность равную (n – столбцовый
ранг), значит, размерность образа равна
n-(n-столбцовый ранг) = столбцовый ранг.
Таким образом строчный и столбцовый ранги матрицы совпадают.
Что и требовалось доказать.
Билет 10. Обратная матрица, теорема о ней.
Матрица В называется обратной матрицей для квадратной матрицы А , если АВ=ВА=Е.
Обратная матрица для матрицы А обозначается А-1. Таким образом, если А-1 существует, то АА-1= А-1А=Е.
Из определения обратной матрицы следует, что матрица А является обратной для матрицы А-1, то есть (А-1)-1=А. Про матрицы А и А-1 можно говорить, что они обратны друг другу или взаимно обратны.
Теорема.
Если
матрица А имеет обратную, то
![]() и
и
![]() .
.
Доказательство.
Так
как определитель произведения матриц
равен произведению определителей, то
![]() .
.
![]() поэтому
поэтому
![]() , что невозможно при
, что невозможно при
![]() . Из предыдущего равенства следует также
.
. Из предыдущего равенства следует также
.
Последнее предложение можно сформулировать в следующем виде.
Если определитель матрицы равен нулю, то обратная к ней не существует.
Так как для нахождения обратной матрицы важно, равен ли определитель матрицы нулю или нет, то введем следующие определения.
Билет 11. Методы решения систем n линейных уравнений с n неизвестными.
С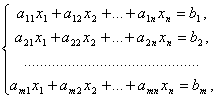 истемой
m линейных уравнений с n неизвестными
называется система вида:
истемой
m линейных уравнений с n неизвестными
называется система вида:
где aij и bi (i=1,…,m; b=1,…,n) – некоторые известные числа, а x1,…,xn – неизвестные.
В обозначении коэффициентов aij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений:
Билет 12. С-мы линейных уравнений общего вида, базисные и свободные переменные.
Если система оказалась совместной, т. е. матрицы A и ` A имеют один и тот же ранг, то могут представиться две возможности - a) r = n; б) r < n:
а) если r = n, то имеем n независимых уравнений с n неизвестными, причем определитель D этой системы отличен от нуля. Такая система имеет единственное решение, получаемое по формулам Крамера;
б) если r < n, то число независимых уравнений меньше числа неизвестных.
Перенесем лишние неизвестные x r+1, x r+2,..., x n, которые принято называть свободными, в правые части; наша система линейных уравнений примет вид:
a 11 x 1 + a 12 x 2 +... + a 1r x r = b 1 - a 1, r+1 x r+1 -... - a 1n x n,
a 21 x 1 + a 22 x 2 +... + a 2r x r = b 2 - a 2, r+1 x r+1 -... - a 2n x n,
... ... ... ... ... ... ... ... ... ...
a r1 x 1 + a r2 x 2 +... + a rr x r = b r - a r, r+1 x r+1 -... - a rn x n.
Ее можно решить относительно x 1, x 2,..., x r, так как определитель этой системы (r-го порядка) отличен от нуля. Придавая свободным неизвестным произвольные числовые значения, получим по формулам Крамера соответствующие числовые значения для x 1, x 2,..., x r. Таким образом, при r < n имеем бесчисленное множество решений.
Билет 13. Системы линейных однородных уравнений. Фундаментальная система решений.
Система из Б.6 называется однородной, если все b i = 0, т. е. она имеет вид:
Из т. Кронекера-Капелли следует, что она всегда совместна, т.к. добавление столбца из нулей не может повысить ранга матрицы. Это видно и непосредственно - система выше обладает нулевым решением x 1 = x 2 =... = x n = 0.
Пусть матрица А системы выше имеет ранг r. Если r = n, то нулевое решение будет ед. решением с-мы выше при r < n с-ма обладает реш-ями, отличными от нулевого, и для их разыскания применяют тот же прием, как и в производственной системе уравнений ФСР.
Фундаментальная система решения - любые линейно независимых решений линейного однородного дифференциального уравнения -ного порядка называется фундаментальной системой решений этого уравнения.
Билет 14. Линейный оператор.
Линейный оператор - обобщение понятия линейного преобразования на линейные пространства. Линейным оператором F на линейном пространстве Е называют функцию F(x), определённую для всех х Î Е, значения которой суть элементы линейного пространства E1, и обладающую свойством линейности:
F((x + (у) = (F(x) + (F(y),
где
х и у — любые элементы из Е, a и b — числа.
Если пространства Е и E1 нормированы
и величина
![]() ограничена, то Л. о. F называют ограниченным,
а
его нормой.
ограничена, то Л. о. F называют ограниченным,
а
его нормой.
Важнейшими конкретными примерами Л. о. в функциональных пространствах являются дифференциальные Л. о.
![]()
и интегральные Л. о.
![]()
примером Л. о. функций многих переменных может служить Лапласа оператор. Теория Л. о. находит большое применение в различных вопросах математической физики и прикладной математики.
15. Собственные векторы и собственное значение матрицы.
относится только к квадр матр: A=(aij)i,j=1,n (наверху черта)
Ненулевой вектор Х наз собств. вектором матр А, if: AX = X
(х Не равен 0-собств вектор, лямбда-любое знач- собств значение).
для нахождения собств знач: (A-E)X=0, получаем с-му ур и составляем по ней опр-ль: a11-λ a12 ... a1n
( A-E) = a21 a22-λ ... a2n = 0
an1 an2 ... ann-λ
это ур-е n-й степени относительно λ – характеристич. ур-е А, (A-E)-характерист многочлен, а его корни – собств знач А. Для нахождения собств векторов в (A-E)X=0 – подставляем найденные знач и решать обычным образом
Билет 16. Линейные и квадратичные формы. Критерий Сильвестра.
Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой.
Пусть квадратичная форма имеет в каком-то базисе матрицу
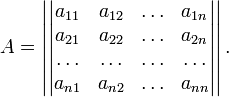
Тогда эта форма положительно определена, если и только если все её главные (угловые) миноры Δi положительны. Форма отрицательно определена, если и только если знаки Δi чередуются, причём Δ1 < 0. Здесь главными минорами матрицы A называются определители вида
![]()

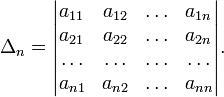
Для неотрицательно определённых матриц критерий действует только в одну сторону: если форма неотрицательно определена, то главные миноры неотрицательны. Обратное неверно. Например, матрица
 не
является неотрицательно определённой
— так как, например, (Mv,v) = − 2 для v = (0,1,
− 1). В то же время все её главные миноры
равны 0, то есть неотрицательны.
не
является неотрицательно определённой
— так как, например, (Mv,v) = − 2 для v = (0,1,
− 1). В то же время все её главные миноры
равны 0, то есть неотрицательны.
Билет 17. Балансовая модель Леонтьева.
Межотраслевой баланс (МОБ, метод «затраты-выпуск») — экономико-математическая балансовая модель, характеризующая межотраслевые производственные взаимосвязи в экономике страны. Характеризует связи между выпуском продукции в одной отрасли и затратами, расходованием продукции всех участвующих отраслей, необходимым для обеспечения этого выпуска. Межотраслевой баланс составляется в денежной и натуральной формах.
Межотраслевой баланс представлен в виде системы линейных уравнений. Межотраслевой баланс (МОБ) представляет собой таблицу, в которой отражен процесс формирования и использования совокупного общественного продукта в отраслевом разрезе. Таблица показывает структуру затрат на производство каждого продукта и структуру его распределения в экономике. По столбцам отражается стоимостный состав валового выпуска отраслей экономики по элементам промежуточного потребления и добавленной стоимости. По строкам отражаются направления использования ресурсов каждой отрасли.
В Модели МОБ выделяются четыре квадранта. В первом отражается промежуточное потребление и система производственных связей, во втором — структура конечного использования ВВП, в третьем — стоимостная структура ВВП, а в четвёртом - перераспределение национального дохода.
Билет 18. Модель международной торговли.
Используемая в настоящее время стандартная модель международной торговли объединяет различные теории, развивающие фундаментальные положения классических теорий на основе использования концепций предельных величин и общего равновесия экономической системы.
Базовые понятия стандартной модели были разработаны английскими экономистами Френсисом Эджуортом и Альфредом Маршаллом и американским экономистом австрийского происхождения Готфридом Хаберлером.
Основы стандартной модели
Стандартная модель, также как и классические теории международной торговли, исходит из того, что мировая экономика представлена двумя странами, в каждой из которых производятся два товара: Х и Y. Кроме того, в стандартной модели используются следующие допущения: покупатели в процессе потребления стремятся обеспечить максимум эффекта (графически это изображается с помощью кривых безразличия), а производители стремятся извлечь максимум прибыли; на внутреннем и мировом рынках существует совершенная конкуренция, в условиях которой равновесная цена устанавливается на уровне, соответствующем предельным издержкам производства
Билет 19. Скалярное, векторное и смешанное произведение векторов.
Скалярное произведение векторов - это операция над двумя векторами, результатом которой является число (не вектор).
Определяется скалярное произведение, как правило, следующим образом:
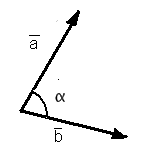
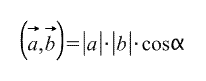
Иными словами, скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними . Необходимо заметить, что угол между двумя векторами - это угол, который они образуют, если отложить их от одной точки, то есть начала векторов должны совпадать.
Векторное произведение двух векторов а и b - это операция над ними, определенная лишь в трехмерном пространстве, результатом которой является вектор со следующими свойствами:

Для большей ясности приведем пример - на рисунке справа вектор [a,b] - векторное произведение векторов а и b. Как сказано в определении, мы привели все три вектора к общему началу, и тогда, если смотреть на вектора a и b с конца вектора [a,b], кратчайший поворот от вектора а до вектора b будет против часовой стрелки .
Смешанное
произведение векторов
![]() — скалярное произведение вектора
— скалярное произведение вектора
![]() на векторное произведение векторов
на векторное произведение векторов
![]() и
и
![]() :
:
![]() .
.
.
Билет 20. Различные виды уравнения прямой на плоскости. Полярная система координат.
Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 не равно 0. Это уравнение первого порядка называют общим уравнением прямой.
В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• А = 0, В ≠0, С ≠0 { By + C = 0} - прямая параллельна оси Ох
• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0 — это уравнение прямой по точке и вектору нормали.
Каждый ненулевой вектор (a1, a2), компоненты которого удовлетворяют условию Аa1 + Вa2 = 0 называется направляющим вектором прямой Ах + Ву + С = 0.
Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом.
Полярная система
координат задаётся лучом, который
называют нулевым или полярной осью.
Точка, из которой выходит этот луч
называется началом координат или
полюсом. Любая точка на плоскости
определяется двумя полярными координатами:
радиальной и угловой. Радиальная
координата (обычно обозначается r)
соответствует расстоянию от точки до
начала координат. Угловая координата,
также называется полярным углом или
азимутом и обозначается
![]() ,
равна углу, на который нужно повернуть
против часовой стрелки полярную ось
для того, чтобы попасть в эту точку.
,
равна углу, на который нужно повернуть
против часовой стрелки полярную ось
для того, чтобы попасть в эту точку.
Билет 21. Угол м/у прямыми. Условия перпендикулярности и параллельности двух прямых.
Условия параллельности двух прямых:
а) Если прямые заданы уравнениями (xcos(альфа)+ysin(альфа)-p=0) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:
k1 = k2.
б) Для случая, когда прямые заданы уравнениями в общем виде (A1x + B1y + C1 = 0, A2x + B2y + C2 = 0), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
![]()
![]()
![]()
Условия перпендикулярности двух прямых:
а) В случае, когда прямые заданы уравнениями (xcos(альфа)+ysin(альфа)-p=0) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
![]()
![]()
![]() k1k2
= -1.
k1k2
= -1.
б) Если уравнения прямых заданы в общем виде (A1x + B1y + C1 = 0, A2x + B2y + C2 = 0), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства A1A2 + B1B2 = 0.
Билет 22. Расстояние от данной точки до данной прямой.
Теорема. Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как
Доказательство. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1:
![]() (1)
(1)
Координаты x1 и у1 могут быть найдены как решение системы уравнений:

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М0 перпендикулярно заданной прямой.
Если преобразовать первое уравнение системы к виду:
A(x – x0) + B(y – y0) + Ax0 + By0 + C = 0,
то, решая, получим:
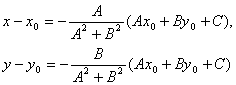
Подставляя эти выражения в уравнение (1), находим:

Теорема доказана!
Билет 23. Кривые второго порядка.
Кривые второго порядка – кривые, описываемые уравнениями второй степени с двумя переменными.
Алгебраической кривой второго порядка называется кривая Г, уравнение которой в декартовой системе координат имеет вид:
Аx2 + 2Вxy + Сy2 + 2Dx + 2Еy + F = 0, где не все коэффициенты А, В и С равны одновременно нулю.
Эллипс - геометрическое место точек, для которых сумма расстояний до двух фиксированных точек (фокусов) есть для всех точек эллипса одна и та же постоянная величина (эта постоянная величина должна быть больше, чем расстояние между фокусами).
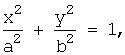
Окружность - замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра).
Гипербола - геометрическое место точек, разность расстояний которых от двух данных фиксированных точек (фокусов) гиперболы есть одна и та же постоянная величина. Предполагается, что эта постоянная величина не равна нулю и меньше, чем расстояние между фокусами.
Простейшее
уравнение гиперболы:
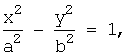
Парабола - геометрическое место точек, каждая из которых одинаково удалена от заданной фиксированной точки и от заданной фиксированной прямой. Точка, о которой идет речь в определении, называется фокусом параболы, а прямая - ее директрисой.
Простейшее уравнение параболы: y2 = 2px.
Билет 24. Каноническое уравнение прямой в пространстве.
Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:
![]()
где
![]() — координаты
— координаты
![]() и
и
![]() направляющего вектора прямой,
направляющего вектора прямой,
![]() и
и
![]() координаты точки, принадлежащей прямой.
координаты точки, принадлежащей прямой.
Вывод:

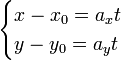
![]()
Билет 25. Плоскость, виды уравнений плоскости.
Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки.
Уравнения плоскости:
Уравнение плоскости в отрезках:
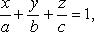 где a, b, c - величины отрезков, отсекаемых
плоскостью на осях координат.
где a, b, c - величины отрезков, отсекаемых
плоскостью на осях координат.
Нормальное уравнение плоскости:
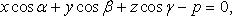 где
где
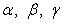 -
углы, образуемые нормальным вектором
плоскости с осями координат; p - расстояние
от начала координат до плоскости.
-
углы, образуемые нормальным вектором
плоскости с осями координат; p - расстояние
от начала координат до плоскости.
