
- •9. Вырожденные и невырожденные матрицы. Ранг матрицы. Теорема о ранге матрицы.
- •Уравнение плоскости по трем точкам:
- •4. Уравнение плоскости по точке и двум неколлинеарным векторам
- •Геометрический смысл предела числовой последовательности
- •Основные свойства сходящихся последовательностей
- •Арифметические действия над последовательностями, имеющими предел
- •1. Бесконечно малые функции при х
- •2. Предел функции при х и его свойства.
- •1. Бесконечно малые функции при х а
- •2. Предел функции в точке
- •3. Односторонние пределы
- •44 Вопрос. Глобальные свойства непрерывных функций.
- •Формула конечных приращений
- •Понятие дифференциала
- •Свойства дифференциала. Инвариантность формы дифференциала
- •51Производные основных элементарных функций
- •53 Вопрос. Логарифмическая производная. Производная функции u(X)V(X).
- •56 Вопрос. Направление вогнутости. Точки перегиба.
- •64 Вопрос. Частные производные и дифференциалы высших порядков. Матрица Гессе.
- •66 Экстремум функции нескольких переменных
- •Билет 70. Неопределенный интеграл. Простейшие свойства.
- •Для неопределённого интеграла
- •Для определённого
- •Метод замены переменной (метод подстановки)
- •72Интегрирование дробно-рациональных функций
2. Предел функции в точке
Определение
3. Число b называют пределом
функции f(х)
при х
а, если f(х)—b является
бесконечно малой функцией при х
а; пишут ![]()
Воспользовавшись для бесконечно малой функции f(х)—b определениями
1 и 2, получим еще два определения, эквивалентные предыдущему.
Определение 4. Число b называют пределом функции f(х) при х а, если для любого > О существует > 0 такое, что из неравенства О < |х—а| < следует неравенство |f(х)—b| < . Короче:
(
>0)(
>0)(![]() :0<|х-а|<
)|f(x)-b|<
.
:0<|х-а|<
)|f(x)-b|<
.
Определение 5. Число b называют пределом функции f(х) при х а, если для любого >0 можно указать такую проколотую -окрестность точки а, в которой выполняется неравенство |f(х) —b|< .
Определение 3 условимся называть определением предела функции в точке «на языке бесконечно малых», определение 4—«на языке е— »,определение 5 — «на языке окрестностей».
3. Односторонние пределы
Определение 6. Число b называется левосторонним пределом функции f(х) при х а, если для любого >0 существует >0 такое, что при всех х из неравенства 0<а—х< следует неравенство |f(x)-b|< .
Число b называется правосторонним пределом функции f(х) при х а, если для любого > 0 существует > 0 такое, что при всех хиз неравенства 0<x—а < следует неравенство |f(x)-b|< .
Билет 42. Непрерывность функции. Классификация точек разрыва.
Функция
![]()
![]() ,
называется непрерывной в точке
,
называется непрерывной в точке
![]() ,
если выполняется одно из эквивалентных
условий:
,
если выполняется одно из эквивалентных
условий:
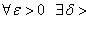
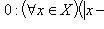

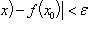 ;
;для произвольной последовательности (xn) значений
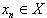 ,
сходящейся при n → ∞ к
точке x0, соответствующая
последовательность (f(xn))
значений функции сходится при n
→ ∞ к f(x0);
,
сходящейся при n → ∞ к
точке x0, соответствующая
последовательность (f(xn))
значений функции сходится при n
→ ∞ к f(x0);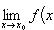
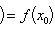 или f(x)
- f(x0)
→ 0 при x - x0
→ 0;
или f(x)
- f(x0)
→ 0 при x - x0
→ 0;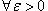
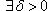 такое,
что
такое,
что
![]()
![]()
![]()
Из определения непрерывности функции f в точке x0 следует, что
![]()
![]()
Если функция f непрерывна в каждой точке интервала ]a, b[, то функция f называется непрерывной на этом интервале.
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
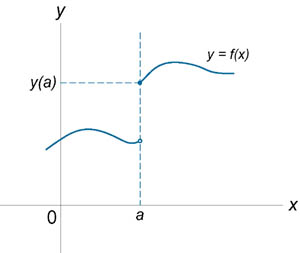
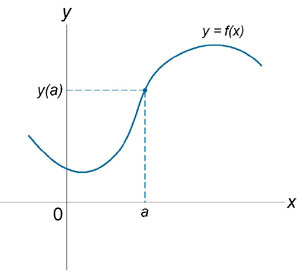
Непрерывна при x = a. Имеет разрыв при x = a.
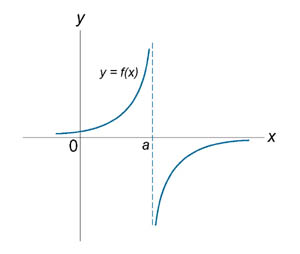
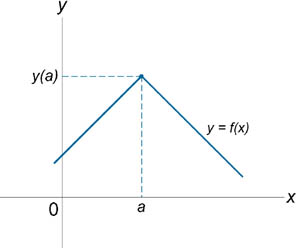
Непрерывна при x = a. Имеет разрыв при x = a.
Классификация точек разрыва функции.
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке.
- Существуют
левосторонний предел
![]() и правосторонний предел
и правосторонний предел
![]() ;
;
- Эти односторонние пределы конечны.
При этом возможно следующие два случая:
- Левосторонний предел и правосторонний предел равны друг другу:
![]()
Такая точка называется точкой устранимого разрыва.
- Левосторонний предел и правосторонний предел не равны друг другу:
![]()
Такая точка
называется точкой конечного разрыва.
Модуль разности значений односторонних
пределов
![]() называется скачком функции.
называется скачком функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
Билет 43. Первый замечательный предел.
Первый
замечательный предел имеет вид:
![]()
На практике чаще встречаются модификации первого замечательного предела в виде
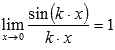 где, k – коэффициент.
где, k – коэффициент.
Пояснение:
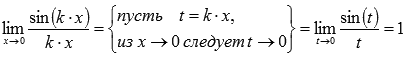
Следствия первого замечательного предела:
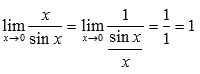
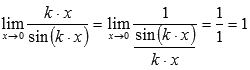
2.
Эти следствия очень просто доказываются, если использовать правило Лопиталя или замену эквивалентных бесконечно малых функций.
