Оценка результатов измерений. Оценка генерального среднего

Предположим, что значение генеральной дисперсии σ известно. Если под случайной величиной Х произведено n измерений, то для оценки генерального среднего используется среднее выборки. Также как и результат единичного измерения, среднее выборки имеет нормальный закон распределения с генеральным средним а и дисперсией σ / n . Строим величину

Она имеет стандартное нормальное распределение. Поэтому при уровне значимости р для этой величины выполняется оценка:

Так как нормальное распределение является симметричным, то

Подставляем сюда значение для U

На практике величина σ не известна. А используется выборочная дисперсия ρ, которая вычисляется по результатам выборки.

Рассмотрим величину

Так как х и ρ есть случайные величины, то и величина t также случайна, но закон распределения для случайной величины t не является нормальным. Этот закон зависит от числа степеней свободы ∂ и называется этот закон распределения распределением Стьюдента. Квантиль этого распределения имеется в таблицах. Т.к. распределение Стьюдента является симметричным, то при данном уровне значимости p справедлива такая оценка:

- число степеней свободы

Подставим сюда значение для t и получим оценку

Если используется односторонняя оценка, то оценка может принимать такой вид:

При больших значениях n, различие между величинами t и u не существенно.

Оценка генеральной дисперсии

Для оценки генеральной дисперсии используется выборочная дисперсия.

В силу случайности выборки выборочная дисперсия S² так же является случайной величиной. Распределение этой случайной величины есть распределение Пирсона или .

В этой сумме есть связь накладываемая на , поэтому число степеней свободы . Именно эта величина имеет распределение Пирсона. Имеются таблицы квантилей этого распределения, с помощью которых мы найдём, что при уровне значимости p, т.е. при доверительной вероятности 1-p для оценки истинного значения величины можно использовать следующее соотношение:

Т.к. выборочную дисперсию можно представить в виде

Отсюда оценку можно представить в виде:

Сравнение дисперсий

Часто возникает вопрос можно ли считать сравниваемые выборочные дисперсии, принадлежащие одной и той же генеральной совокупности. Предположим, сравниваются две выборочные дисперсии S₁² и S₂², которым соответствует ν₁ и ν₂ , пусть первой выборочной дисперсии (S₁²) соответствует σ₁², а второй (S₂²) – σ₂². Выдвигается гипотеза о равенстве дисперсий, чтобы отвергнуть эту гипотезу надо установить значимость различия между выборочными дисперсиями. Рассмотрим величину:

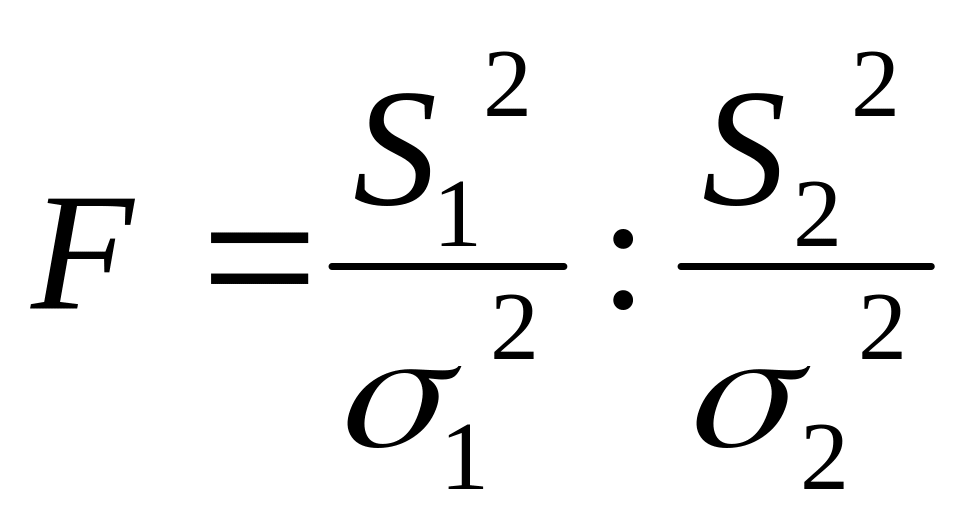
Эта величина случайная, распределение этой случайной величины не является нормальным, а называется распределением Фишера. Оно зависит от двух значений степеней свободы. Для квантилей этого распределения справедливо свойство:

В предположении справедливости этой гипотезы

;

;

Возможны односторонние оценки, например

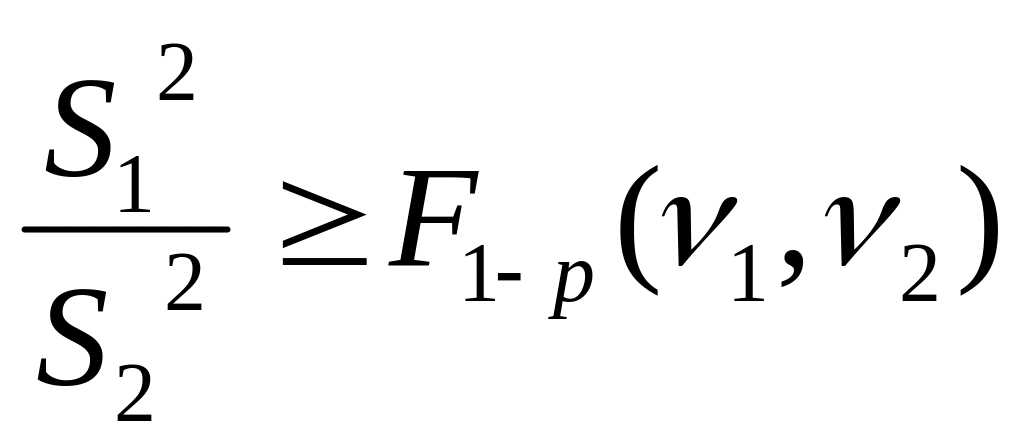
Если эти оценки не выполняются, то нулевая гипотеза отвергается, т.е. считается доказанным, что дисперсии не равны. Если же это условие выполняется, то основания для отвержения гипотезы нет.

Сравнение среднего

Пусть даны две выборки:

x₁, x₂, … x_n;

y₁, y₂, … y_m;

Этим выборкам соответствуют генеральные средние а₁ и а₂ , и генеральные дисперсии σ₁ и σ₂.

Рассмотрим величину:

Эта случайная величина имеет нормальный закон распределения со следующими характеристиками:

Отсюда следует, что величина

является нормированной случайной величиной, имеющей нормальное распределение, поэтому будит справедливо соотношение:

Отсюда получим оценку для разности а₁-а₂

Аналогичным образом можно получить одностороннюю оценку.

Если это соотношение выполняется, то это говорит, что различие между средними является незначимым. Эта оценка применяется в том случае, если известны значения генеральных дисперсий.

Если генеральные дисперсии не известны, то вместо нормального распределения используется распределение Стьюдента.

Предположим вначале, что σ₁²=σ₂². Эта гипотеза проверяется по известным значениям выборочных дисперсий по критерию Фишера.

Для оценки генеральной дисперсии можно брать средневзвешенную выборочную дисперсию.

;

Величина

является нормальной случайной величиной. Заменяя в этой величине генеральную дисперсию (σ) на выборочную (S), мы получим случайную величину, имеющую распределение Стьюдента и в этом случае будет справедлива оценка:

Если

,

то это соотношение говорит, что различие между этими величинами значимы и . Эту оценку можно использовать только в том случае, если генеральные дисперсии равны. Если же на самом деле , то полученные критерии оказываются непригодными. В этом случае для проверки гипотезы о равенстве средних можно поступить следующим образом:

Вычисляется две величины

, ,

а затем вычисляется величина

Нулевая гипотеза отвергается, если выполняется соотношение

.

В отличие от предыдущего метода , такой способ оценки является более грубым.