Проведение факторного эксперимента и обработка его результатов

После того как составлена матрица планирования эксперимента, приступают к его проведению при этом необходимо учитывать погрешность измерений. Оценить погрешность можно по парным опытам. Каждое значение у находится несколько раз, и находится среднее всех результатов.

Затем для каждой серии опытов оценивается дисперсия

Если требуется, то необходимо исключить результаты, содержащие грубую ошибку. Для этого возможно использование τ-критерия.

Матрицу планирования можно использовать для оценки дисперсии всех опытов. Если число повторных измерений одинаково, то для оценки результирующей дисперсии можно использовать:

На практике число повторных измерений может различаться. Это может происходить из-за отбрасывания результатов содержащих грубую ошибку. В этом случае результирующую средневзвешенную дисперсию вычисляем таким образом:

ν_i-число степеней свободы для опыта с N_i

При вычислении дисперсий представляется их однородность. Это справедливо когда среди дисперсий σ_i нет сильно различающихся. Если возникают сомнения то необходимо проверить гипотезу о неоднородности дисперсии, используя критерий Фишера.

Если дисперсии однородны, то рассчитывается погрешность воспроизводимости и погрешности для коэффициентов модели. Для устранения или уменьшения систематических погрешностей необходимо производить рандомизацию порядка проведения опытов.

Продемонстрируем значение рандомизации на следующем опыте. Пусть проводится ПФЭ типа 2³. В матрице планирования будет записано 8 опытов. Пусть первые 4 опыта проводятся в 1 день, а остальные 4 в другой. Изменившиеся условия могут привести к тому, что во второй день возникает системная погрешность = Е.

№	Х0	Х1	Х2	Х3	У
1	+	+	+	+	У1+Е
2	+	-	+	+	У2+Е
3	+	+	-	+	У3+Е
4	+	-	-	+	У4+Е
5	+	+	+	-	У5
6	+	-	+	-	У6
7	+	+	-	-	У7
8	+	-	-	-	У8

В результате для коэффициента а₃ линейной модели получается значение:

а₃=1/8(у₁+Е+ у₂+Е+ у₃+Е+ у₄+Е-у₅- у₆- у₇- у₈)=1/8(у₁+ у₂+ у₃+ у₄-у₅- у₆- у₇- у₈)+Е/2

После проведения всех опытов вычисляются коэффициенты модели. Для этого используется метод наименьших квадратов, который приводит к формулам вида:

После вычисления коэффициентов а_i необходимо проверить адекватность полученной модели, ее пригодность. Для этого вычисляется дисперсия адекватности с помощью формулы:

где N-число опытов

n-число коэффициентов в модели

у_i-значение полученное экспериментально

у_im= а₀+а₁х₁⁽²⁾+ а₂х₂⁽²⁾+…

Для проверки гипотезы об адекватности модели вычисляется величина

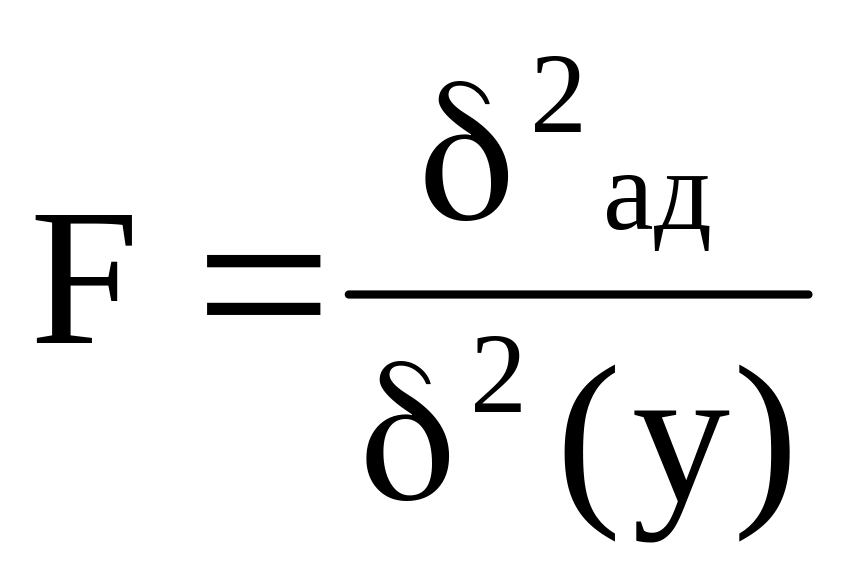
и сравнивается с соответствующим квантилем распределения Фишера. Если величина меньше квантиля то полученная модель является адекватной, в противном случае модель необходимо уточнить, включая в нее новые члены, учтенные эффекты более высокого порядка или дополнительные факторы.

После получения адекватной модели необходимо проверить

Шалимов

Значимость отдельных коэффициентов модели. Для этого в качестве оценки дисперсии для коэффициентов регрессии

Далее вычисляют критерий Стьюдента

И сравнивают его с табличным значением.

Если эта величина оказывается меньше соответствующего квантиля.

Планирование эксперимента при поиске оптимальных условий

Эффективность некоторого процесса, например, производственной деятельности может характеризоваться с помощью некоторой функции, называемой целевой функцией или функцией отклика, зависящей от ряда параметров y = y(x₁, x₂, x₃, …, x_к).

Задачей оптимизации является нахождение значений параметра х_1oп, x_2oп, … x_коп обеспечивающих максимум целевой функции. Возможно, при выполнении дополнительных условий, которые запишем следующим образом:

Возможный путь нахождения решения в проведении факторного эксперимента для определения параметров функции отклика, после чего производить поиск экстремума этой функции. Однако, в этом случае требуется построение поверхности отклика в широком интервале варьирования. При этом функция отклика становится существенно нелинейной и требует построения сложной математической модели. Что требует большой объем эксперимента и трудоемкие вычисления.

В этом случае используют методы последовательного пошагового измерения поверхности отклика.

Схема такая:

Выбирается исходная точка проведения эксперимента и ставится небольшая серия опытов с целью изучения экспериментального участка поверхности отклика, т. к. рассматриваемый участок небольшой, то для поверхности отклика можно использовать линейную модель.

А для построения линейной модели достаточно проведения факторного эксперимента на двух уровнях.

После нахождения параметров линейной модели, определяется направление движения к оптимальному решению, оно совпадает с направлением градиента целевой функции (или имеет противоположное направление).

Для линейной модели компоненты градиента совпадают с коэффициентами линейной модели.

После нахождения коэффициентов линейной модели производится шаг в направлении градиента, в результате мы попадаем в новую точку, в которой процедура повторяется.

(Определяется новая небольшая область и т. д.).

Процесс движения повторяется до тех пор, пока мы не попадем в почти стационарную область вблизи оптимального решения.

Здесь ставится большая серия опытов с целью более точного описания поверхности отклика.

Для повышения эффективности поиска оптимального решения, используется метод крутого восхождения, метод Бокса-Уилсона.

В этом методе вычисление градиента после каждого шага не производится, а производится движение в направлении градиента до тех пор, пока происходит рост целевой функции.

Почти стационарная область содержит точку оптимума и поэтому не может быть описана линейной моделью. Для ее описания обычно используют полиномы второго порядка. В этом случае составляется план, в котором каждая переменная принимала бы по крайней мере три различных значения, т. е. строится план типа 3^k.

Такое планирование может быть получено путем добавления некоторых точек специальным образом подобранных к ядру, образованному планированием линейной модели, такие планы называются композиционными или последовательными. Число экспериментов для композиционных планов меньше чем число экспериментов ПФЭ 3^k.

Рассмотрим случай k = 3.

При k = 3, число экспериментов измерений равно 27.

N	X1	X2	X3
1	+1	+1	+1	23-1
2	-1	+1	+1
3	+1	-1	+1
4	-1	-1	+1
5	0	0	0
	+1	+1	-1	23-1
	-1	+1	-1
	+1	-1	-1
	-1	-1	-1
		0	0	звездные
	0		0
	0	0

x₂

Всего 15 точек вместо 27. Для большего числа фактора эффект уменьшения более заметный вместо 3^k будет .

Необходимо выбрать оптимальное значение α, оно выбирается таким образом, чтобы обеспечить ортогональность вектор-столбцов и ортогональность матрицы планирования. В силу ортогональности, коэффициенты регрессии будут определяться по известным нам формулам.

ядро	22	23	24
α	1,0	1,215	1,414

Проведем сравнение активного оптимального эксперимента с классическим для двух факторов.

Эксперимент начинается с исходной точки и в (методе покоординатного спуска).

Особенности классического эксперимента следующие:

1. Часть эксперимента производится впустую, в ошибочном направлении.

2. Поиск ведется практически вслепую методом попыток.

3. Движение к оптимуму не является кратчайшим.

4. С увеличением числа факторов процедура поиска оптимума резко усложняется.

1. В активном эксперименте ставится минимальное количество опытов.

2. Движение к оптимуму производится кратчайшим путем.

3. Наряду с оптимальным решением находится уравнение для поверхности отклика.

58