33. Необходимые условия существования максимума и минимума функций
Пусть
точка
является точкой экстремума функции
,
определенной в некоторой окрестности
точки
.Тогда
либо производная
не
существует, либо
.
Если больше нуля, решение есть.
34. Достаточные условия существования экстремума функций.
Первое достаточное условие экстремума.
Если
в точке
функция
непрерывна и в ней производная меняет
знак с плюса на минус, то
-
точка максимума.
Если в точке функция непрерывна и в ней производная меняет знак с минуса на плюс, то - точка минимума. ОБРАТИТЕ ВНИМАНИЕ: первый достаточный признак экстремума не требует дифференцируемости функции в самой точке .
Второе достаточное условие экстремума.
Пусть
,
если
,
то
-
точка минимума;
если
,
то
-
точка максимума.
Третье достаточное условие экстремума
Пусть
функция y
= f(x)
имеет производные до n-ого
порядка в
-окрестности
точки
и
производные до n+1-ого
порядка в самой точке
.
Пусть
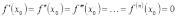и
.
Тогда,
если n
– четное, то
-
точка перегиба; если n
– нечетное, то
-
точка экстремума.
Причем,
если
,
то
-
точка минимума;
если
,
то
-
точка максимума.
35. Экстремумы функций нескольких переменных
Точка М(Хо,Yо) называется точкой максимума (минимума) функции z=f(x,y),если существует окрестность точки M, такая, что для всех точек (х,у) из этой окрестности выполняется неравенство f(Xo,Yo) больше или равно (меньше или равно) f(x,y).
Необходимое условие экстремума: в точке минимума или максимума дифференцируемой функции градиент (вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины) равен нулю. Равенство частных производных нулю выражает лишь необходимое, но недостаточное условие экстремума функции нескольких переменных.
Если определитель функции меньше нуля, то экстремума нет.
Если равно нулю, однозначного решения нет.
Если больше нуля, решение есть.
36.Раскрытие неопределенности вида . Теорема 1 Лопиталя (при , при ).
Неопределенность вида -это отношение двух функций f(x)/g(x), где lim f(x),при x→a=lim g(x),при x→a=0.
Раскрыть неопределенность – значит найти предел этого отношения.
Теорема Лопиталя 1.
Пусть f(x) и g(x) определены на (а;в] и lim f(x)при x→a=lim g(x)при x→a=0. И на этом же промежутке f'(x) и g'(x) ≠ 0, тогда lim f(x)/g(x)при x→a=lim f'(x)/g'(x) при x→a.
Теорема Лопиталя 1'
Пусть f(x) и g(x) определены на [с;∞] и lim f(x)при x→∞=lim g(x)при x→∞=0. И если на этом же промежутке f'(x) и g'(x) ≠ 0, тогда lim f(x)/g(x)при x→∞=lim f'(x)/g'(x) при x→∞.
37.Раскрытие неопределенности вида . Теорема 2 Лопиталя (при , при ).
Теорема Лопиталя 2.
Пусть f(x) и g(x) определены на (а;в] и lim f(x)при x→а=lim g(x)при x→а. И если на этом же промежутке f'(x) и g'(x) ≠ 0, тогда lim f(x)/g(x)при x→а=lim f'(x)/g'(x) при x→а
Теорема Лопиталя 2'.
Аналогично теореме 2: lim f(x)/g(x)при x→∞=lim f'(x)/g'(x) при x→∞.
38.Раскрытие неопределенности вида
Такие
виды неопределенностей решаются
сведением к неопределенностям вида
,
.