1.Алгебраическое дополнение
Алгебраическим дополнением (Аij) элемента матрицы (аij),называется его минор, взятый со знаком (-1)^i+j.
2. Минор матрицы
Минор матрицы (Mij) элемента матрицы А называется определитель матрицы (n-1) порядка, полученной из матрицы А вычеркиванием i-строки и j-столбца.
3.Обратные матрицы
Матрица называется обратной по отношению к квадратной матрице А, если при их перемножении мы получаем единичную матрицу А*А^(-1)=Е
4.Ранг матрицы
Рангом матрицы называется наивысший порядок отличных от нуля миноров матрицы. Ранг показывает количество линейно-зависимых строк.
Элементарные преобразования матриц
1.Отбрасывание нулевых строк или столбцов.
2.Умножение строки или столбца на число не равное нулю.
3. Изменение порядка следования строк или столбцов, предварительно умноженных на некоторое число.
ТЕОРЕМА: ранг не меняется при элементарных преобразованиях.
5.Решение систем линейных уравнений методом Гаусса.
СЛУ сводится к ступенчатому виду. Выписываем расширенную матрицу. Ранг равен числу неизвестных.
Решение СЛУ с формулами Крамера.
Пригодны только если m=n.
Ищем определитель. Находим 1=определитель исходной матрицы ,где первый столбец заменен на ответы. Теперь 2 по такой же схеме , но второй столбец заменяем на ответы. Последнее : x = 1 \ определитель (А) : у = 2 \ А
Решение СЛУ с помощью обратных матриц.
Применяемо, если m=n , определитель не равен нулю и А*х =В. Обе части уравнения умножаем слева на обратную матрицу: ( (А^(-1) * A)\E) * x= A ^(-1)*B ; E*x= (A^(-1))*B ; x=A^(-1)*B.
Сначала ищем определитель. Затем обратную матрицу, а после все по формулам.
6.Собственные векторы и собственные значения.
Вектор называют собственным вектором матрицы А, если найдется число λ не равное нулю такое, что А*х = λ* х, число λ – собственное значение матрицы А.
(А - λ*Е)=0
Уравнение |А-λ*Е|=0 называется характеристическим уравнением матрицы А, корни этого уравнения (λ) есть собственные значения матрицы А.
7.Прямоугольная и полярная система координат на плоскости.
Полярная система координат задается центром О (полюсом) и лучом Ор (полярная ось) с указанием единицы. Каждая точка определена двумя числами – полярным углом и полярным радиусом.
Прямоугольная система координат образуется двумя перпендикулярными осями х и у , они пересекаются в точке О (начало координат). Х- абсцисса, У – ординат.
8. Длина вектора. Угол между векторами.
Два вектора равны ,если равны их координаты.
Длина
вектора
в
пространстве равна корню квадратному
из суммы квадратов его координат, то
есть, находится по формуле
.
Угол
между векторами: По определению
скалярное произведение векторов есть
.
Если векторы
и
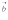ненулевые, то можно разделить обе части
последнего равенства на произведение
длин векторов
и
,
и мы получим формулу для нахождения
косинуса угла между ненулевыми векторами:
.
9. Ортогональные и ортонормированные векторы.
Вектор а и b называют ортогональным, если их скалярное произведение равно 0.
А и B называют ортонормированными, если их скалярное произведение равно 0, а длины 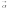1.
=
=1
,
┴
10. Уравнения прямой на плоскости.
1. y=kx+b ,k=y-b\x – прямая
2. A(Xo,Yo), y= kx+b , Y-Yo=K(X-Xo) - уравнение прямой ,проходящей через точку (Хо,Уо)
3. У-Уо\Уо-У1= Х-Хо\Хо-Х1 – прямая, проходящая через две точки.
4. Уо=У1 У=Уо (прямая параллельная оси абцисс)
Хо=Х1 Х=Хо (прямая параллельная оси ординат)
5 . y\b +x\a= 1 – уравнение прямой в отрезках.
6. A(X-Xo)+B(Y-Yo)=0 –прямая, проходящая через точку
11. Расстояние
между точками А
(х1;
у1)
и В (х2;
у2
)
:
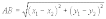
12.Деление
отрезка в заданном отношении
-
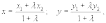
где А (х1; у1) и В(х2; у2) — концы отрезка, точка C(x ,y) делит АВ в отношении
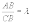
13.Линии второго порядка на плоскости
Кривая второго порядка может быть задана уравнением : Ах2 + 2Вху + Су2 + 2Dx + 2Ey + F = 0.
Эллипс-множество точек плоскости ,сумма расстояний от каждой из которых, до двух данных точек, называемых фокусом, есть величина постоянная большая чем расстояние между фокусами.
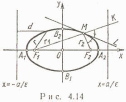
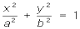
Гипербола-это множество точек плоскости, модуль разности расстояний от каждой из которой до двух дальних (называемых фокусом) есть величина постоянная меньшая, чем расстояние между фокусами.
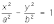
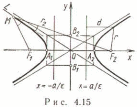
Окружность : Окружность радиуса R с центром в начале координат:
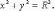
Уравнение
касательной к окружности в произвольной
точке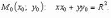 
Параметрические
уравнения: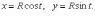 
Окружность
радиуса R с
центром в точке C(a;
b):
