14.Комплексные числа. Сумма, произведение, частное, возведение в степень, извлечение корня.

Комплексные числа - это числа вида Z= , где х и у любые действительные числа и это мнимая единица, то есть i ² = –1.

1.  Действительное число  а  может быть также записано в форме комплексного числа:  a+ 0 i или  a – 0 i.  Например, записи  5 + 0 i  и  5 – 0 i  означают одно и то же число  5 . 

2.  Комплексное число 0+ bi  называется чисто мнимым числом. Запись bi означает то же самое, что и  0+ bi.

3.  Два комплексных числа  a+ bi  и c+ di считаются равными, если  a= c и b= d. В противном случае комплексные числа не равны.

Сложение:

Произведение:

Частное:

Возведение в степень:

  Операцию возведения в степень удобнее выполнять, когда комплексное число записано в тригонометрической или в показательной форме.

Извлечение корня:

Значения   , отличные от указанных в этой формуле, дадут те же значения   , которые можно получить при .

15. Замечательные пределы: 1-й, 2-й, 3-й.

Первым замечательным пределом называется предел

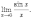
Первый замечательный предел равен

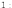
Вторым замечательным пределом называется предел

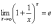
Число часто называют основанием натуральных логарифмов. Второй замечательный предел существует. Его значение -- число, лежащее между и .

Более подробное изучение числа показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:

Третий замечательный предел.

(1/n и n поменять местами! 1/n-степень, n-в скобках)

16. Теорема Коши

Если функции и непрерывны на отрезке и дифференцируемы во всех его внутренних точках, причем не обращается в ноль ни в одной из указанных точек, то существует, по крайней мере, одна точка , такая что:

.

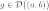, и

17. Теорема Ферма

Функция у= f(x) определена на промежутке (а,б) и во внутренней точке С принадлежащей промежутку (а,б) принимает наибольшее /наименьшее значение, тогда если в этой точке существует конечная производная, то она равна 0. f'(С) = 0

18. Теорема Ролля

Пусть функция у = f(x) определена и непрерывна на промежутке [а, в] и дифференцируема на открытом промежутке (а,в) и на концах [а, в] принимает равные значения, тогда существует точка С такая, что производная в этой точке = 0.

19. Теорема Лагранжа

Пусть функция у= f(х) определена и непрерывна на (а,в), тогда найдётся точка С, такая что

f(C) = ; = tg α(альфа)

20.Определение непрерывности функции в точке и на промежутке.

а) Функция у = f(х) называется непрерывной в точке х0,если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции :

Б) Функция у = f(х) называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка.

21.Непрерывность элементарных функций.

Все элементарные функции непрерывны в области их определения.

Множество основных элементарных функций включает в себя:

Алгебраические многочлены

Рациональные дроби

Степенные функции

Показательные функции

Логарифмические функции

Тригонометрические функции

Обратные тригонометрические функции

22.Классификация разрывов.

Точка х₀ называется точкой разрыва функции f(x), если f(x) не определена в точке х₀ или не является непрерывной в этой точке.

Точка х₀ называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

 Точка х₀ называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.