§39. Правило перемежаемости корней

Это правило является следствием критерия Михайлова и позволяет при n  6 обойтись без построения кривой Михайлова.

Так как кривая Михайлова строится при возрастании частоты, то для частот пересечения с осями должно выполнятся неравенство ₀<₁<₂<₃ ... Примем во внимание, что ₀, ₂, ₄ – вещественные неотрицательные корни уравнения

N() = 0 , (1)

а ₁, ₃, ₅ – положительные вещественные корни уравнения

M() = 0 , (2)

обозначенные по их возрастанию.

Сравнивая неравенство с обоз-начениями корней, сформулируем правило:

Для устойчивости системы необходимо и достаточно, чтобы вещественные неотрицательные корни уравнений (1) и (2), полученных из мнимой и вещественной функции Михайлова, чередовались (перемежались), т. е. между корнями уравнения (1) на числовой оси должны располагаться корни уравнения (2).

Ввиду того, что остальные корни этих уравнений имеют отрицательный знак, они также чередуются, поэтому нет надобности их рассматривать. При наличии мнимых или комплексных корней в этих уравнениях система неустойчива, так как кривая Михайлова не пересекает нужное число раз соответствующую ось.

Например, для данной кривой Михайлова

N() = 0 имеет два корня, а M() = 0 вещественных корней не имеет (отсутствие

пересечения с мнимой осью), значит система неустойчива.

Корни уравнений (1) и (2) можно определить графически построив вещественную и мнимую функции Михайлова .

С ледует обратить внимание, что при использовании данного правила уравнения (1) и (2) решаются отдельно, в то время как при нахождении граничных значений параметров эти уравнения решаются совместно.

§40. Критерий устойчивости Найквиста

Данный критерий позволяет исследовать устойчивость замкнутой системы (ЗСАР) по АФХ соответствующей разомкнутой системы (РСАР), причем АФХ может быть получена, как аналитически, так и экспериментально.

Вывод формулы критерия. Для вывода рассмотрим комплексную функцию частоты

, где - ЧПФ РСАР.

Подставляя ЧПФ в предыдущее равенство получим

,

где D(j) - характеристический комплекс РСАР,

A(j) - характеристический комплекс ЗСАР.

Степень многочлена D выше, чем степень многочлена Q, поэтому старшие степени характеристических комплексов D и A одинаковы и равны n (порядку уравнения данной системы).

Применив к последнему равенству правило и принцип аргументов, получим

,

где l, m - число правых корней характеристических уравнений разомкнутой (D(s)=0) и замкнутой (A(s)=0) САР соответственно.

Геометрический смысл.

Комплекс F(j)=1+W(j) можно рассматривать как вектор на комплексной плоскости АФХ, который имеет начало в точке (-1; j0) и оканчивается на АФХ РСАР.

Соответственно изменение arg F(j) можно определить как угол поворота вектора F(j) при изменении  от нуля до .

Если этот угол составляет 2 рад, то это означает, что АФХ охватывает точку (-1; j0), как начало этого вектора, один раз в положительном (отрицательном) направлении. Если результирующий угол поворота , то имеет место половина охвата в том или ином направлении. Если результирующий угол 0, то АФХ не охватывает точку (-1; j0), которая называется опасной (с точки зрения устойчивости).

Формулировки и примеры применения критерия

В соответствии с рассмотренным геометрическим смыслом из формулы критерия вытекают его формулировки для двух случаев:

1. Если РСАР устойчива (l=0), то для устойчивости замкнутой системы (m=0) необходимо и достаточно, чтобы АФХ разомкнутой системы не охватывала опасную точку при изменении  от 0 до .

2. Если РСАР неустойчива и ее характеристическое уравнение имеет l правых корней, то для устойчивости ЗСАР необходимо и достаточно, чтобы АФХ РСАР охватывала опасную точку l/2 раз в положительном направлении.

Пример 1. Статическая система 3 -го порядка

САР в разомкнутом состоянии устойчива, т.к. её характеристическое

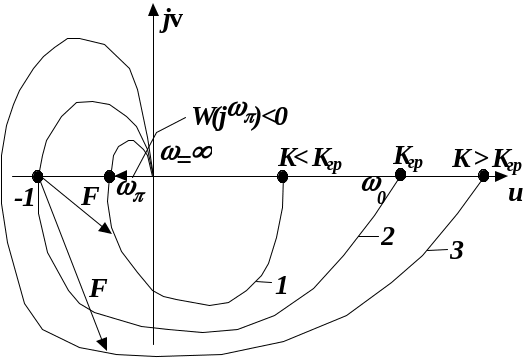
уравнение (T₁s+1)(T₂s+1)(T₃s+1)=0; имеет левые корни ; Значит l=0 и применять следует первую формулировку.

Построим АФХ РСАР для ряда значений коэффициента усиления К разомкнутой системы. При К<Кгр (кривая 1):

,

где _ - частота, при которой  (_)=  .

В соответствии с первой формулировкой делаем вывод, что ЗСАР устойчива, т.к. АФХ РСАР не охватывает опасную точку.

Допустим, что К возрос настолько, что характеристика прошла через опасную точку (кривая 2). Для этой характеристики argF определить нельзя , т. к. в характеристическом уравнении ЗСАР имеются мнимые корни  j_ , а в этом случае принцип аргумента не применим, и замкнутая система находится на колебательной границе устойчивости. Располагая характеристикой 1, граничное значение К_гр можно определить из пропорции:

. Отсюда

При К > К_гр АФХ охватит опасную точку (кривая 3) один раз в отрицательном направлении, т. к. . В этом случае ЗСАР неустойчива, причем в соответствии с основной формулой принципа аргумента (l - m)= -2 при l = 0 получим m = 2, т. е. два правых корня и один левый в характеристическом уравнении ЗСАР.

Пример 2. РСАР имеет п. ф.

В этом случае РСАР неустойчива, и в её характеристическом уравнении один правый корень (l=1). Используем вторую формулировку критерия.

Построим АФХ РСАР для двух случаев T₁ > T₂ ; T₁ < T₂. Соответственно из графиков найдем:

Этот результат можно проверить, записав характеристическое уравнение замкнутой системы.

Критерий может применяться к системам, характеристическое уравнение которых в разомкнутом состоянии имеет корни на мнимой оси. Здесь возможны два случая. В первом из них астатическая система, содержащая несколько интегрирующих звеньев, имеет п. ф. в разомкнутом состоянии , где v - число интегрирующих звеньев и нулевых корней характеристического уравнения РСАР. АФХ такой системы при   0 уходит в , т. е. контур АФХ разомкнутый. Для того, чтобы применить критерий Найквиста, делается предположение о том, что нулевые корни смещаются на бесконечно малую величину влево. На устойчивость замкнутой системы это не влияет и поэтому допустимо. Благодаря этому смещению интегрирующие звенья превращаются в инерционные первого порядка, и АФХ, как следствие, получает дополнение в бесконечности до вещественной оси в виде дуги бесконечно большого радиуса, стягивающей в пределе угол . После этого может быть применена 1-я или 2-я формулировка критерия в зависимости от корней уравнения D₁(s)=0.

Пример 3. Астатическая система, содержащая одно интегрирующее звено (v=1), имеет в разомкнутом состоянии п.ф.

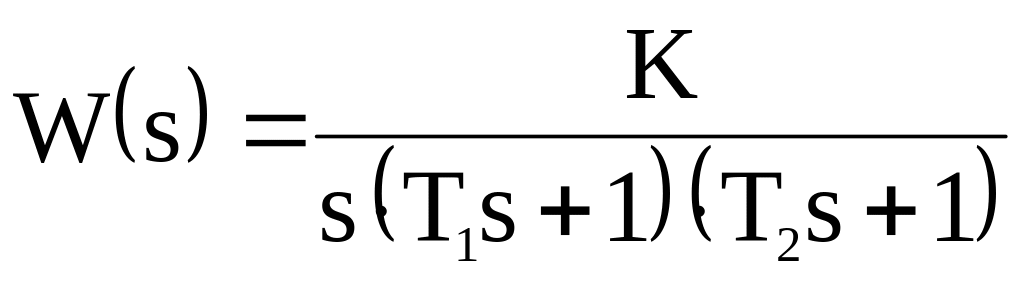
Результат анализа ясен из графика: ЗСАР устойчива.

Второй случай характеризуется наличием одной или нескольких пар мнимых корней в характе-ристическом уравнении РСАР за счет присутствия в ее структуре консервативных звеньев.

АФХ имеет разрыв 2 рода при .

Предполагается, что мнимые корни смещаются на бесконечно малую величину влево, что соответствует преобразованию консервативных звеньев в колебательные и дополнению АФХ дугами бесконечно большого радиуса, стягивающими углы  в каждом месте разрыва 2-го рода АФХ, при движении от отрезка с большими частотами к отрезку с меньшими частотами.

Пример 4. Задана п.ф. РСАР. характеристическое уравнение, которое имеет два мнимых корня.

АФХ имеет разрыв второго рода при ₀=1/T₀ . В месте разрыва

производим дополнение в бесконечности. После этого делаем вывод, что при <T₁ ЗСАР неустойчива т.к. АФХ охватывает опасную точку. При >T₁ ЗСАР устойчива.

К примеру 3 К примеру 4