§32. Необходимое условие устойчивости

Это условие требует, чтобы все коэффициенты характеристического уравнения были одного знака - положительного. Для доказательства характеристический полином после вынесения можно представить в виде произведения простых сомножителей (теорема Безу):

,

где s_i – i–тый корень характеристического уравнения.

Если подставить сюда значения только левых корней, то после перемножения получатся коэффициенты характеристического уравнения одного знака с ( всегда можем сделать >0), что и требовалось доказать.

Для систем первого и второго порядка необходимое условие является в то же время и достаточным, в чем можно убедиться, выразив корни через коэффициенты.

§33. Общая характеристика критериев устойчивости

Критерий устойчивости - правило, позволяющее без решения характеристического уравнения, т. е. без нахождения корней, исследовать устойчивость систем при двух основных постановках задачи:

1) при заданных значениях всех параметров решается вопрос об устойчивости САР (прямая задача);

2) обратная задача, при которой определяются значения одного или нескольких параметров, при которых система устойчива или находится на границах устойчивости.

В последнем случае значения варьируемых параметров называются граничными (критическими, предельными).

Особо важное значение имеет граничный коэффициент усиления разомкнутой системы, при котором замкнутая система находится на границе устойчивости .

Критерии устойчивости целесообразно использовать по двум причинам:

1. для исследования устойчивости нет надобности определения корней,

достаточно знать их распределение относительно оси , т.е. мнимой оси;

2. уравнения выше третьего порядка в общем случае не решаются в радикалах (отсутствует формула выражения корней через коэффициенты уравнений).

Все критерии устойчивости делятся на два вида:

• алгебраические

• частотные

Они отличаются по своим алгоритмам, но выражают необходимые и достаточные условия устойчивости.

§34. Алгебраические критерии устойчивости

Эти критерии предполагают выполнение алгебраических операций над коэффициентами характеристического уравнения. По результатам операций делаются выводы об устойчивости.

1. Критерий Вышнеградского И.А. относится только к уравнениям 3-го порядка:

.

Приводим уравнение к нормализованному виду, для чего вначале делим его почленно на :

.

Вводим затем новую переменную: . После преобразований получим нормализованное уравнение:

,

где X,Y – могут быть выражены через коэффициенты исходного уравнения.

Условием устойчивости является XY>1. При XY=1 САР находится на колебательной границе устойчивости, а линия с уравнением XY=1, отображающая границу устойчивости на плоскости XY, носит название гиперболы Вышнеградского.

35. Критерий Гурвица предполагает составление и вычисление определителей Гурвица из коэффициентов характеристического уравнения.

Главный определитель Гурвица Δ_n имеет n-ый порядок, где n старшая степень характеристического уравнения. По его главной диагонали записывают коэффициенты от a₁ до a_n, где a₁ – коэффициент при производной (n-1) - го

порядка. Вверх от главной диагонали столбцы заполняются коэффициентами с последовательно возрастающими индексами, а вниз - с последовательно убывающими, причем вместо отсутствующих коэффициентов ставят нули. Поэтому в последнем столбце кроме a_n будут только нули.

Определители младшего порядка получаются как диагональные миноры определителя Δ_n:

, ,..., .

Критерий Гурвица требует, чтобы все определители Гурвица были больше нуля (при условии, что >0). Если хотя бы один определитель меньше нуля, то система неустойчива . Система находится на колебательной границе устойчивости при совместном соблюдении следующих условий:

1. необходимое условие ,

2. ,

3. ,

4. .

Из третьего условия, как главного для данного случая, находим граничные значения параметров и проверяем выполнение условий 1 и 2.

Апериодическая граница устойчивости требует:

1. ,

2. ,

3. ,

4. .

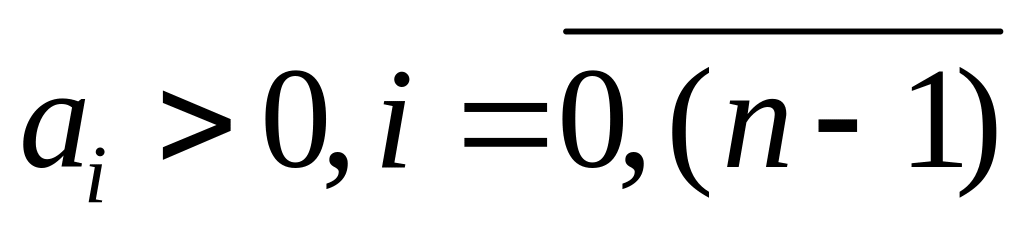Второе условие главное, и из него находится граничное значение того или иного параметра, после чего проверяется выполнение условий 1 и 3.

Для практики условие апериодической границы устойчивости обычно менее существенно, так как оно дает нижнюю границу коэффициента усиления.

Применение данного критерия в принципе не ограничено порядком, однако сложность вычисления определителя возрастает с увеличением n. Для n=3 и n=4 кроме выполнения необходимого условия устойчивости достаточно исследовать знак только определителя Δ_n-1.

36Критерий Рауса предполагает составление таблицы Рауса и исследование знака элементов ее первого столбца.

Вспом. коэфф-т.	№стлб №стр	1	2	3	.............
---------	1				..............
---------	2				..............
	3			............	..............
.............	...........	...................	..................	............	............
rn-1­	n-1	cn-1,1	an	0	0
rn	n	cn,1	0	0	0
----------	n+1	cn+1,1=an	0	0	0

Вспомогательные коэффициенты определяются как отношение элементов 1-го столбца 2-х предыдущих строк. Элементы третьей и последующих строк находятся с использованием вспомогательного коэффициента через элементы следующего столбца двух предыдущих строк.

В последней (n+1)-й строке только один элемент ненулевой. Система устойчива, если все элементы 1-го столбца таблицы Рауса больше нуля при условии >0. Если хотя бы один элемент 1-го столбца таблицы меньше нуля, то система неустойчива, причем число перемен знака у элементов первого столбца равно числу правых корней характеристического уравнения.

Система находится на колебательной границе устойчивости, если предпоследний элемент первого столбца равен нулю, а остальные положительны. Данный критерий имеет преимущественное применение для систем высокого порядка, причем все вычисления выполняются на ЭВМ и их сложность с увеличением порядка не повышается.