§37. Частотные критерии устойчивости. Принцип аргумента

Эти критерии основаны на построении тех или иных частотных характеристик. Общей базой для частотных критериев служит принцип аргумента. Этот принцип позволяет по изменению аргумента комплексной функции частоты определить распределение корней соответствующего уравнения относительно мнимой оси.

Пусть имеется характеристический многочлен А(s) исследуемой на устойчивость системы. Требуется найти формулу, которая позволяла бы найти распределение корней уравнения A(s)=0 относительно мнимой оси. Для вывода этой формулы представим многочлен в виде простых сомножителей (теорема Безу):

,

где s_i – i – тый корень уравнения A(s)=0.

Сделав частотную подстановку , получим характеристический комплекс:

. Применим к этому комплексу известное правило аргументов:

.

Каждое слагаемое суммы, образующей правую часть формулы, найдем геометрически как угол поворота соответствующего вектора. Рассмотрим два случая: - левый и - правый корень (корни на мнимой оси должны отсутствовать).

Из графика следует:

jω

+π

α

-π

Допустим, что в исследуемом уравнении n–го порядка имеется m - правых и n-m - левых корней. Тогда общая формула для приращения аргумента будет следующая:

.

Если вдвое уменьшить диапазон изменения частоты , то вдвое уменьшится изменение аргумента, что приводит к следующей формуле принципа аргумента:

.

Практическое применение принципа предполагает геометрическое построение годографа вектора A(jω) при 0≤ω≤∞ и определение изменения его аргумента, как изменения угла его поворота, затем применяется полученная формула и при известном n определяется m.

§38. Критерий устойчивости Михайлова а. В.

Этот критерий является графическим вариантом принципа аргумента для устойчивой системы, т.е. при m=0. В этом случае из формулы принципа аргумента следует .

Данный критерий, как правило, применяют к замкнутой системе, но в общем случае он может быть применен и к разомкнутой системе.

Во всех случаях находится характеристический многочлен как знаменатель соответствующей передаточной функции .

Затем в этот характеристический многочлен делается частотная подстановка и получается характеристический комплекс в алгебраической или показательной форме:

,

где , R()=modA(j).

Затем по полученной формуле необходимо построить годограф характе-ристического вектора на комплексной плоскости M,jN. Для этого частоту необходимо изменять от 0 до с малым шагом, предварительно определив точки пересечения годографа с осями координат. Этот годограф называется кривой Михайлова.

Если учесть, что изменение аргумента характеристического вектора на соответствует прохождению кривой Михайлова через один квадрант комплексной плоскости, то можно дать следующую формулировку критерию:

Система устойчива, если при изменении  от 0 до кривая Михайлова, начинаясь на вещественной полуоси, проходит последовательно n квадрантов комплексной плоскости, начиная с первого и не проходя через начало координат.

Кривые Михайлова для устойчивых САР разного порядка показаны на рисунке.

Все кривые уходят в бесконечность, причем вдоль той полуоси, которая определяется наибольшим по модулю слагаемым .

Если последовательность прохождения квадрантов кривой Ми­хайлова нарушена, то система неустойчива, причем по принципу ар­гумента можно определить распределение корней характеристиче­ского уравнения. Например, для заданного годографа графически найдем

=0

С другой стороны

.

Так как n=4, то m=2 и САР неустойчива.

При нахождении системы на границе устойчивости кривая Михайлова должна удовлетворять следующим двум условиям:

1) кривая проходит через начало координат комплексной плоскости (или исходит при наличии нулевого корня). Действительно, в этом случае характеристическое уравнение имеет корни на мнимой оси (нулевой или мнимые). Значит соответствующие значения частоты (=0, =_i ) обращают характеристический комплекс в 0.

Для нахождения граничных значений параметров и соответствующих мнимых корней достаточно решить систему уравнений

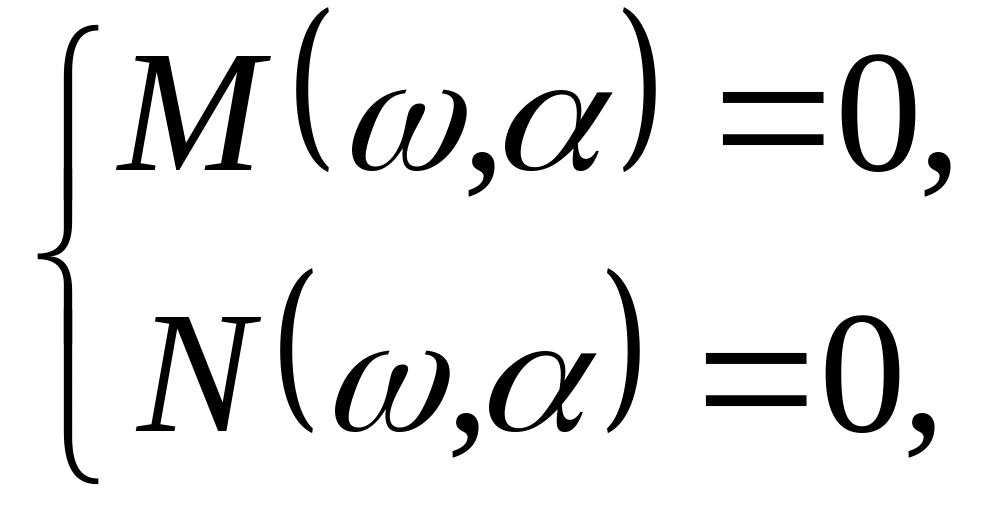
где  - варьируемый параметр, а M и N вещественная и мнимая функции Михайлова. Эта система выражает первое условие;

2) бесконечно малая деформация кривой в окрестности начала координат может сделать систему устойчивой. Для n =3 и n=4 второе условие всегда соблюдается и специальной проверки не требует;

Примеры. Заданы кривые Михайлова, проходящие через начало координат, бесконечно малые деформации показаны условно штриховыми линиями. Требуется исследовать устойчивость.

3) Сар неустойчива, т.к. последовательность прохождения квадрантов нарушена, в характеристи-ческом уравнении имеются 2 правых корня.