Тема №3. Устойчивость линейных непрерывных систем

§31. Понятие устойчивости и его связь с распределением корней характеристического уравнения

Устойчивость является необходимым условием работоспособности САР.

Система называется устойчивой, если после снятия возмущения она возвращается к первоначальному установившемуся режиму работы.

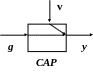
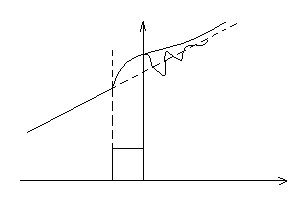
Допустим, что в течение некоторого отрезка времени до t=0 на систему действовало возмущение v(t). До приложения возмущения под влиянием задающего воздействия y изменялось, например, по линейному закону. Это и есть первоначальный установившийся режим.

После снятия возмущения, т.е. при t>0 в устойчивой системе y(t) должно стремиться к . Это может происходить апериодически или колебательно в виде затухающих колебаний (кривые 1 и 2 соответственно ).

Условие устойчивости:

. (1)

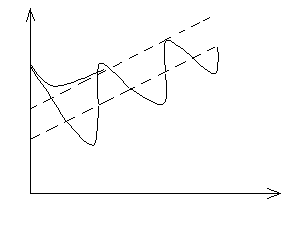
Система неустойчива, если после снятия возмущения выходная величина неограниченно удаляется от первоначального установившегося режима. Это удаление может происходить монотонно (кривая 3), или в виде расходящихся колебаний (кривая 4).

t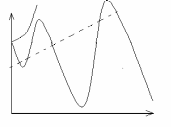

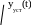Система находится на апериодической границе устойчивости, если при в ней сохранится постоянное отклонение y(t) от y_уст(t) (кривая 5). Система находится на колебательной границе устойчивости, если в ней устанавливаются колебания постоянной амплитуды относительно y_уст(t) (кривая 6).

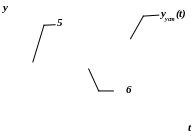
Допустим, что исследуемая система имеет характеристическое уравнение n-го порядка

a₀sⁿ+ a₁s^n-1+…+ a_n-1s+ a_n=0.

Изменение у(t) после снятия возмущения является с математической точки зрения общим решением соответствующего неоднородного дифференциального уравнения, а следовательно состоит из двух составляющих - установившейся и переходной:

y(t)= y_уст(t)+ y_пер(t). (2)

Как известно из классического метода, переходная составляющая является общим решением соответствующего однородного уравнения (без правой части) и определяется корнями s_i характеристического уравнения в соответствии с формулой:

. (3)

Подставляя (3) в (2) , а (2) в (1) получим условие устойчивости в виде

. (4)

Сумма, входящая в (4), будет тогда стремиться к 0, когда каждое ее слагаемое стремится к 0:

. (5)

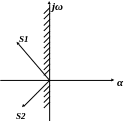
Условию (5) удовлетворяют корни, имеющие отрицательную вещественную часть. Такие корни на комплексной плоскости изображаются в виде точек или векторов в левой полуплоскости и поэтому называются левыми корнями. Следовательно, устойчивая система должна иметь в своем характеристическом уравнении только левые корни.

Если хотя бы один корень характеристического уравнения имеет положительную вещественную часть (правый корень), то система неустойчива. Система неустойчива также в том случае, если в характеристическом уравнении имеется два и более нулевых корней. При нулевом корне r-той кратности в переходной составляющей присутствует сумма вида C₀+ C₁t+…+C_r-1t^r-1, стремящаяся к бесконечности, что и указывает на неустойчивость.

Система находится на апериодической границе устойчивости при наличии одного нулевого корня при остальных левых корнях.

Система находится на колебательной границе устойчивости при наличии одной или нескольких пар мнимых корней при остальных левых (частоты незатухающих колебаний определяются модулями мнимых корней ).