Зоны Френеля

Ф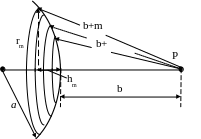 ренелем был предложен метод зон Френеля, которые позволят рассчитывать амплитуду простым алгебраическим суммированием. По выражению (4.1) рассчитывать очень сложно. Этот метод удобен в случаях симметричного распространения световых волн. Рассмотрим на примере сферической волны от точ. источника S . Найдем амплитуду в точке Р. Световые волны симметричны относительно SP.

Суть метода зон Френеля состоит в разбиении волновой поверхности на кольцевые зоны, расстояние от краев соседних зон до Р отличаются на . Следовательно, результирующие колебания, создаваемые каждой из зон в целом, для соседних зон будут отличаться по фазе на  (то есть в противофазе).

Рассчитаем площади зон

Площадь зоны m

- площади сферических сегментов ( ).

Из рисунка

r_m – радиус внешней границы

h_m – высота сегмента

(4.2)

При небольших m слагаемым пренебрежем.

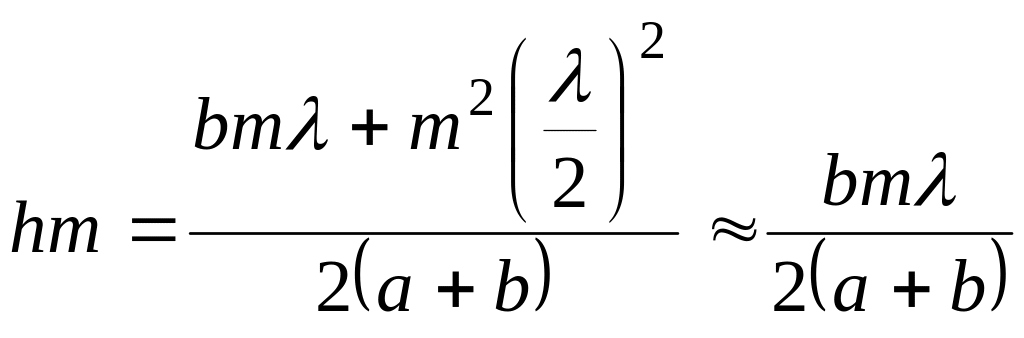(4.3)

Тогда

Так как не зависит от m, то при небольших m площади зон примерно одинаковы.

При малых m и в выражении (4.2) членом пренебрежем

(4.4)

Если положить

Так как уменьшается при увеличении m, то амплитуда возбуждается зоной в точке Р с увеличением m убывает.

Так как колебания от зон приходят в противофазе, то результат амплитуды:

Если ее записать как

и положить, что

то

Таким образом, амплитуда, создаваемая сферической волной в точке Р. равна половине амплитуды, создаваемой первой зоной Френеля. Если в экране оставить отверстие под 1 зону Френеля, то амплитуда будет А₁, то есть в 2 раза больше, чем А. А интенсивность в 4 раза будет больше.

Если перекрыть все четные или нечетные зоны Френеля, то интенсивность в точке Р резко возрастает. Такая платинка называется зонной. Есть фазовая зонная платинка, которая изменяет фазу, допустим, нечетных зон Френеля на . Усиление интенсивности в 4 раза (амплитуда в 2 раза).

Дифракция от круглого отверстия

Пусть на пути сферической волны находится экран с круглым отверстием радиуса . Тогда из формулы (4.4)

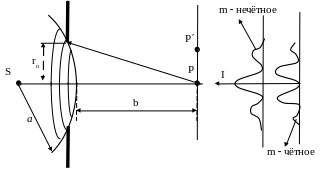(4.5)

Картина разная в зависимости четное или нечетное m. Амплитуда в точке Р будет равна

(Если m – нечетное, то «+»).

Если m – нечетное, то

- увеличение амплитуды

Если четное, то

- уменьшение.

Если открыть нечетное количество зон, то будет наблюдаться усиление амплитуды в 2 раза, интенсивности в 4 раза.

Дифракция от круглого диска

Если диск закрытых m зон Френеля (рассчитывается по формуле (4.5)), то

,

о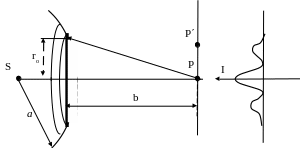 ткуда . При m малом .

Дифракция Фраунгофера

Пусть на бесконечно длинную щель падает плоская волна. За щелью поместим линзу и экран так, что экран лежит в фокальной плоскости линзы. Так как щель бесконечна, достаточно рассмотреть дифракцию в одной плоскости, перпендикулярной щели.

Разобьем волновую поверхность в щели на зоны шириной , которые параллельны краям щели. Вторичные волны, посылаемые зонами в направлении, определяемом углом , соберутся в точке Р экрана. Так как линза собирает в фокальной плоскости плоские волны, то в (4.0) отсутствует. Ограничимся рассмотрением малых углов , тогда коэффициент К будем считать постоянным. Тогда согласно принципу Гюгенса-Френеля каждая зона создает в точке Р колебания с амплитудой

(4.6)

, зависящей только от площади зоны

Обозначим через А₀ алгебраическую сумму амплитуд, возбуждаемую в точке Р всеми зонами.

Ее можно найти, проинтегрировав по всей щели в

,

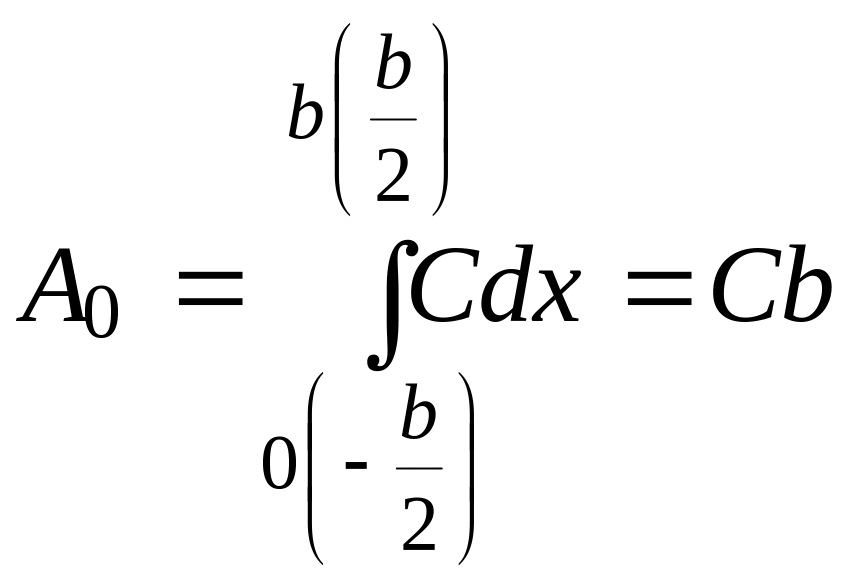о ткуда (4.6) Сопоставим фазы возбуждаемых колебаний в точке Р зонами с координатами О и Х. Оптические пути ОР и QP таухотронны. Следовательно, разность фаз образуется на пути . Если начальную фазу колебаний в точке О принять равной 0, то начальная фаза колебаний, возбуждаемых зоной с координатой х , будет равна

(4.8)

Тогда, подставив (4.7), (4.8) в (4.6), получим колебания, создаваемые зоной с координатой Х

где .

Проинтегрировав выражение по ширине зоны, найдем результирующее колебание в точке Р, создаваемое волновой поверхностью в пределах щели:

Интегрирование дает

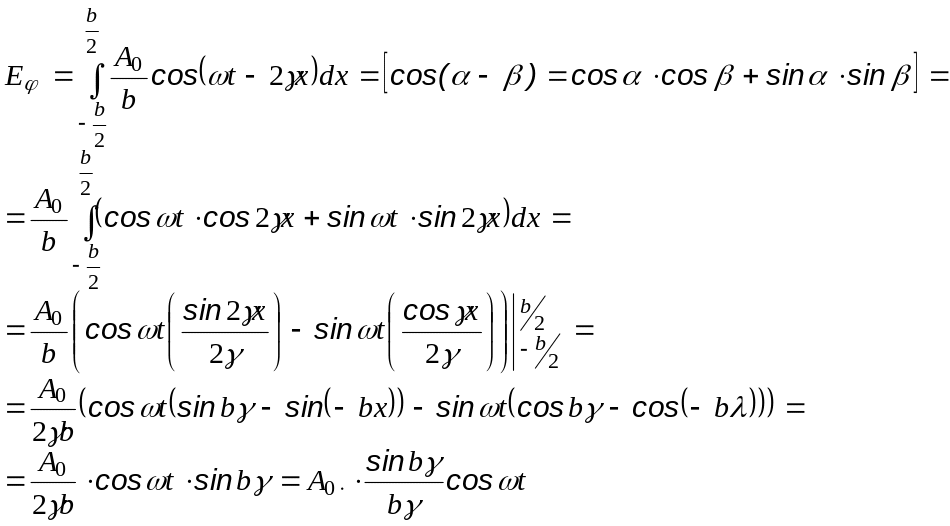
При

1. замечательный предел ( при )

при

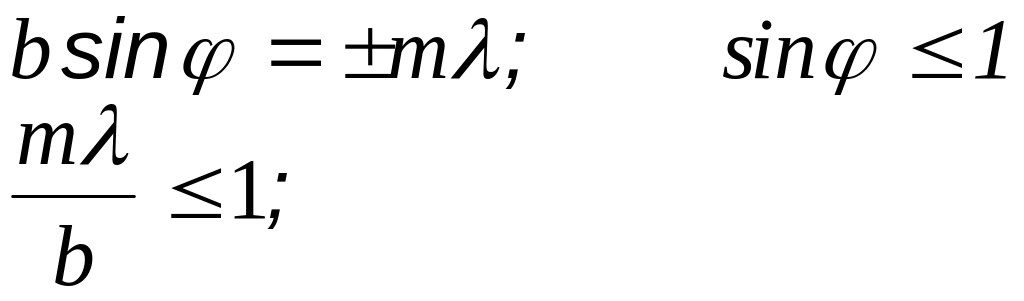
- количество минимумов

Таким образом, поле интегрирования получаем:

,

где (4.10)

- есть амплитуда колебаний .

при (то есть точка Р напротив щели)

- первый замечательный предел и результирующая амплитуда равна .

Минимальная амплитуда будет при (m=1,2,3…) – условие минимумов интенсивности.

- оптическая разность хода лучей от краев щели.

Учитывая, что интенсивность из 4.10 получим для интенсивности в точке Р

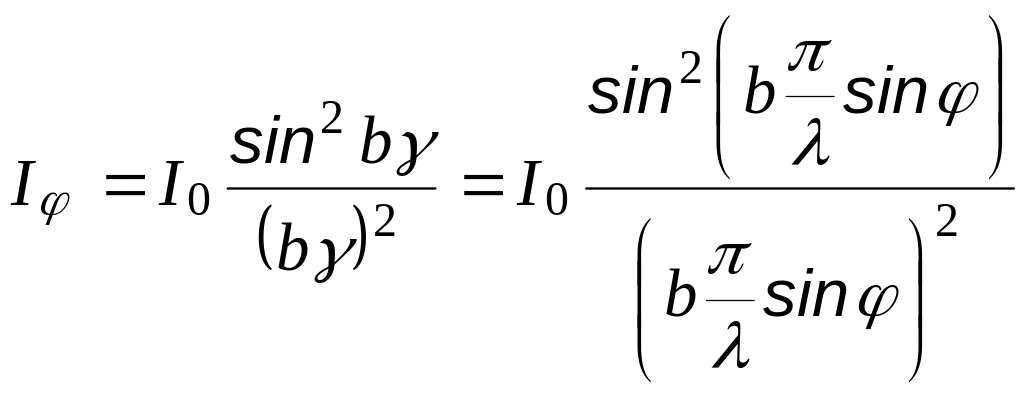(4.12)

Из 4.12, так как и следует , то есть картина симметрична относительно центра линзы.

Если изобразить график интенсивности

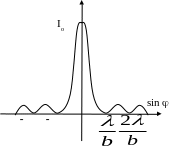
Из (4.11) можно найти количество минимумов интенсивности (т.к.

То есть когда ширина щели минимумов вообще не возникает.

Краям центрального максимума соответствуют углы следующие из условия : эти значения равны , откуда угловая ширина центрального максимума при .