Т ак как очень мало (1,05  10-34 Дж  с), то соотношение неопределенностей проявляет себя ярко в микромире.

Поясним соотношение неопределенностей из следующего примера. Пусть на пути частицы расположена щель - ширина щели. Определим координату х частицы. Перед щелью х – совершенно неопределенна, а .

При пролете через щель координата определена с точностью , а импульс приобретает за счет дифракции электрона неопределенность . Считая для щели условие максимумов для волнового процесса с , получим

по порядку величины совпадает с .

Учитывая, что из соотношения Гейзенберга

Это соотношение показывает, что чем больше m, тем меньше неопределенность x и , тем с большей степенью точности можно говорить о понятии траектории микрочастицы.

Волновая функция

ЛЕКЦИЯ № 9

Временное и стационарное уравнение Шрёдингера

Де Бройль сопоставил свободно движущейся частице плоскую волну (смысл которой сначала был не ясен).

Заменив и на р и Е уравнение волны де Бройля пишут в виде:

Функцию называют волновой функцией, (по Борну) квадрат которой определяет вероятность нахождения частицы в пределах объема

- комплексно сопряженная .

- выражает плотность вероятности нахождения частицы в соответствующем месте пространства.

Интеграл по всему пространству дает 1:

- и называют условием нормировки

На - функцию налагают стандартные условия: она должна быть непрерывной, однозначной, конечной, иметь непрерывную и конечную производную.

Таким образом, квантовая механика имеет статистический характер, она определяет лишь вероятность нахождения частицы в данной точке пространства.

Волновая функция является решением уравнения Шрёдингера, полученным им в 1926 оду Общий вид его:

(2)

m – масса частицы

- мнимая частица

U – потенциальная энергия частицы

- оператор Лапласа

Это уравнение не выводится и получено Шредингером из оптико-механической аналогии уравнений светового луча и траекторий движения частиц.

Можно придти к уравнению Шредингера следующим образом:

Пусть движется свободная частица, тогда

вдоль Х. (U = 0)

Тогда ;

Выразив Е и р², получим:

Учтя, что , получим

совпадает с (2) при U = 0

В случае, если силовое поле. В котором движется частица стационарно (U не зависит от t) то волновую функцию можно разбить на две части, зависящую от координат и времени.

При подстановке во временные уравнения Шредингера (2) и после сокращения на придем к уравнению Шрёдингера для стационарных состояний

(3)

или

Теперь плотность вероятности

В связи с принципом неопределенности и введением волновой функции принцип причинности в квантовой механике видоизменяется. Если по силовому полю и начальным условиям решая уравнения Ньютона в классической механике мы определяем положение и скорость частицы, то в квантовой механике, зная волновую функцию и силовое поле можем найти волновую функцию при помощи уравнения Шредингера в любой момент времени.

Различие в поведении квантовых и классические частиц проявляется в том случае если на пути частицы встречается потенциальный барьер (при , при )

Для классической частицы: если Е – полная энергия частицы меньше U₀ то она не преодолеет и, потеряв часть скорости, будет двигаться вдоль Х.

Для квантовой частицы: если ,она проникнет на некоторую глубину, а затем начнет двигаться обратно.

Г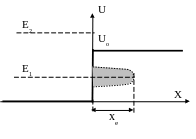 лубиной проникновения . при которой вероятность нахождения частицы уменьшается в е раз

Например, металлическое тело для свободных электронов является потенциальной ямой с U₀, которая выше Е электрона на 1 эВ. Тогда Å.

Поверхность металла является потенциальным барьером, который электроны преодолевают на глубину и возвращаются обратно. Следовательно, поверхность металла окружена облаком электронов

Даже если , то (возможно) есть вероятность отражения частицы от барьера

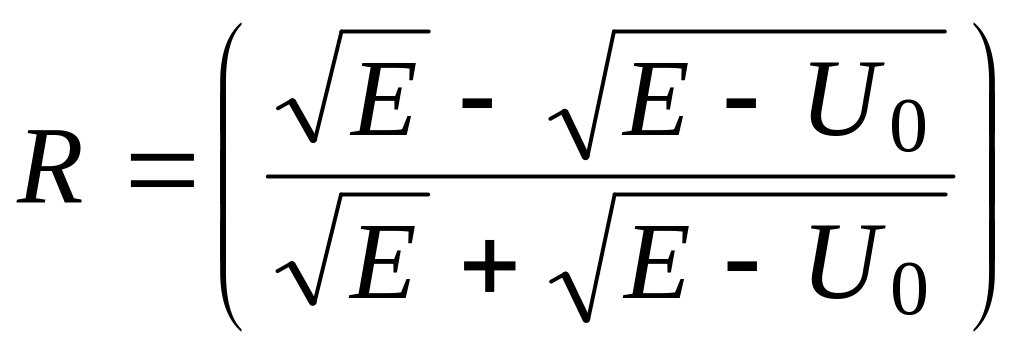
Д ля барьера конечной ширины вероятность того, что квантовая частица пройдет барьер называется коэффициентом прохождения (прозрачности)

Для барьера произвольной формы

Ч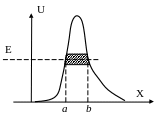 астица как бы проходит через «туннель» в потенциальном барьере и поэтому такое явление называется туннельным эффектом.

В туннеле получается, что кинетическая энергия отрицательна. Такого быть не может, так как одновременно знать кинетическую и потенциальную энергию в квантовой механике невозможно, то же самое, что одновременно и x, следовательно, понятие отрицательной кинетической энергии абсурдно.