20. Т.1 Всякая формула, получающаяся из тавтологии

алгебры высказываний заменой входящих в нее пропозициональных

переменных произвольными предикатными переменными, является

тавтологией логики предикатов.

Теорема(законы пронесения кванторов через импликацию).

Следующие формулы логики предикатов яв-ся тав-ями:

а) ( х)(Р(х) −> Q) <−> (( х)(Р(х)) −> Q);

б) ( х)(Р(х) −> Q) <−> (( x)(P(x))−> Q);

в) ( x)(Q −> Р(х)) <−> (Q −> ( x)(P(x)));

г) ( x)(Q −> P(x)) <−>(Q −> ( х)(Р(х))).

Доказательство. Отметим, что предикатная переменная Q

в этих формулах может быть не только нульместной, но и любой

«n-местной, важно лишь, чтобы в нее не входила предметная

переменная х. Итак, пусть Q есть Q(y1…yn). Будем считать для

краткости, что Q есть одноместная предикатная переменная Q(y).

Тогда:

а) предположим, что данная формула не является тавтологией.

В этом случае существуют такие конкретные предикаты А(х) и

В(у), определенные на множествах М и М1 соответственно, что

предикат (от у)

( х)(А(х) −> В(у)) <−> (( х)(А(х)) −> В(у))

опровержим, т.е. обращается в ложное высказывание при

подстановке вместо предметной переменной у некоторого конкретного

предмета b e М{:

λ[( х)(А(х) −> В(b)) <−> (( х)(А(х)) −> В(b))] = 0.

Эквивалентность ложна, если ее члены принимают разные

значения истинности, т.е. здесь могут представиться две возможности:

первая

λ [( х)(А(х) −> В(b))] = 1; (1)

λ [( х)(А(х)) −> В(b)] = 0 (2)

и вторая

λ [( х)(А(х) −> В(b))] = 0; (3)

λ [( х)(А(х)) −> B(b)] = 1. (4)

Рассмотрим первую возможность. Из формулы (2), по определению импликации, имеем

λ [( х)(А(х))] = 1; (5)

λ [В(b)] = 0. (6)

Далее, из формулы (5) и по определению квантора

существования заключаем, что предикат А(х) выполним, т.е.

λ [А(а)] = 1 (7) для некоторого а Є М. Вернемся к соотношению (1). По

определению квантора общности предикат А(х) −> В(b)

тождественно истинен. В частности, если вместо предметной переменной х

подставить а Є М, то получим истинное высказывание λ [А(а) −> B(b)] = 1. Но, учитывая (6) и (7), получаем λ [А(а) −> В(b)] = λ [А(а)] −> λ [В(b)] = 1 −> 0 = 0. Противоречие.

Рассмотрим вторую возможность, выраженную в

соотношениях (3), (4). Из формулы (3), на основании определения квантора общности, следует, что предикат А(х) −> В(b)

опровержим, т.е. λ [А(а) −> В(b)] = 0 для некоторого а Є М. Тогда по

определению импликации получим

λ [А(а)] = 1, λ [В(b)] = 0. (8)

Учитывая второе из соотношений (8), из соотношения (4)

заключаем, что λ[( х)(А(х))] = 0. Последнее означает

тождественную ложность предиката А(х). В

частности, для предмета а Є М имеем λ [А(а)] = 0, что противоречит

первому из соотношений (8).

Итак, в каждом случае приходим к противоречию,

Следовательно, данная формула — тавтология.

21.Две ф-лы логики предикатов А и В наз=-я равносильными на области М, если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области М.

Две формулы логики предикатов А и В наз-ся равносильными, если они равносильны на всякой области.

Ясно, что все равносильности алгебры выск-ий будут верны, если в них вместо переменных выск-ий подставить ф-лы логики предикатов. Но, кроме того, имеют место равносильности самой логики предикатов. Рассмотрим основные из этих равносильностей.

Пусть А(х) и В(х) – переменные предикаты, а С – переменное выск-ие. Тогда имеют место равносильности:

1.

2.

3.

4.

5. 6. 7.

8.

9.

10. 11.

12.

13. 14.

15. Говорят, что ф-ла логики предикатов имеет приведенную нормальную форму, если она содержит только операции конъ-ции, дизъ-ции и кванторные операции, а операция отрицания отнесена к элементарным ф-лам.

Т.1.Для каждой формулы логики предикатов сущ-ет приведенная форма.

22. Предваренной нормальной формой для ф-лы логики предикатов наз-ся такая ее приведенная форма, в к-ой все кванторы стоят в ее начале, а область действия каждого из них распространяется до конца ф-лы, т.е. эта ф-ла вида , где -есть один из кванторов или (i=1…m), m≤n, причем формула F не содержит кванторов и является приведенной формулой.

Т.1. Для каждой ф-лы логики предикатов сущ-ет предваренная нормальная форма. Док-во: док-во по индукции, следуя правилу построения формул логики предикатов. Если ф-ла атомарна, то она сама представляет собой предваренную нормальную форму. Поскольку каждая формула F равносильна формуле,полученной из более простых формул F и F с помощью простых формул (операции →и↔ выражаются через и ), то теперь остается найти предваренные нормальные формы для формул ¬F …F F …F F ..,( )(F ),( )(F ), если известны предваренные нормальные формы F и F формул F и F соответственно.Пусть F имеет вид , а F имеет вид . Рассмотрим формулу ¬F .Поскольку F F , то¬F ¬F . Но ф-ла ¬F ,в свою очередь равносильна ф-ле . Предваренная норм.форма для F, если F есть (F F ). F F F F . F F равносильна формуле 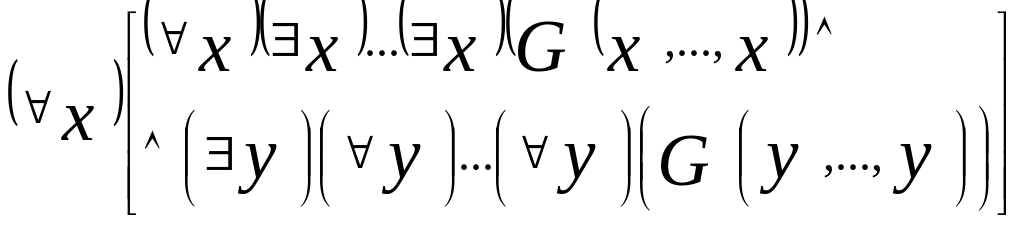.Кванторы, стоящие перед ф-лой G ,выносятся за квадратные скобки.В рез-те получаем ф-лу 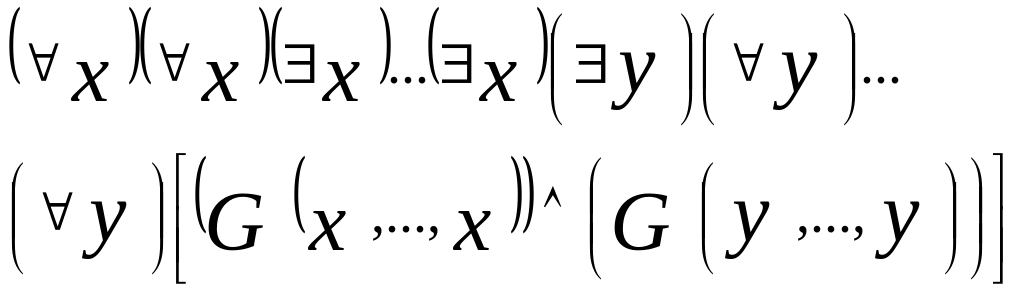, равносильную формуле F F и являющуюся предваренной нормальной формой этой ф-лы.

Ф-ла равносильна ф-ле и явл-ся ее предваренной норм.формой. -предваренная норм.форма для ф-лы .Итак в каждом случае F обладает предваренной норм.формой.

23. Решение проблемы для формул на конечных множествах. Если ф-ла логики предикатов рассматривается на конечном множестве, то вместо ее предикатных переменных могут подставляться конкретные предикаты,определенные на этом конечном мн-ве.На конечных мн-вах вопрос о разрешимости решается положительно, т.к.операции квантификации на конечном мн-ве сводятся к конъюнкции и дизъюнкции: на конечном мн-ве М={a ,…,а }.

а) пусть -истинное выск-ие.Тогда Р(х)-тождественно истинный предикат.Сл-но, замена предметной переменной х любым предметом из М превратит Р(х) в истинное выск-ие,конъ-ция ист-ых выск-ий также будет ист-ым выск-ием.

б) пусть -ложное выск-ие. Тогда Р(х)-тождественно ложный предикат. Сл-но, замена предметной переменной х любым предметом из М превратит Р(х) в ложное выск-ие,дизъ-ция ложных выск-ий также будет ложным выск-ием.

Ф-ла А логики предикатов наз-ся выполнимой в области М, если существуют значения переменных входящих в эту ф-лу и отнесенных к области М, при к-ых ф-ла А принимает истинные значения.

Ф-ла А логики предикатов наз-ся выполнимой, если существует область, на к-ой эта ф-ла выполнима.

Ф-ла А логики предикатов наз-ся тождественно-истинной в области М (выполнимой), если она принимает истинные значения для всех значений переменных, входящих в эту ф-лу и отнесенных к этой области.

Ф-ла А логики предикатов наз-ся общезначимой, если она тождественна истинна на всякой области (на любой модели).

Из приведенных определений с очевидностью следует:

1.Если ф-ла А общезначима, то она и выполнима на всякой области (модели).

2.Если ф-ла А тождественно истинна в области М, то она и выполнима в этой области .

3.Если ф-ла А тождественно ложна в области М , то она не выполнима в этой области .4.Если ф-ла А не выполнима, то она тождественно ложна на всякой области (на всякой модели).

5.Для того, чтобы ф-ла А логики предикатов была общезначима, необходимо и достаточно, чтобы ее отрицание было не выполнимо.

6.Для того, чтобы ф-ла А логики предикатов была выполнимой, необходимо и достаточно, чтобы ф-ла была не общезначима.

24.Формальная теория наз-ся семантически непротиворечивой, если ни одна из ее теорем не явл-ся противоречивой,т. е. ложной при любой ее интерпретации. Формальная теория Г называется синтаксически (или дедуктивно, или формально) непротиворечивой, если не существует такой формулы F, что F и -\F являются теоремами теории Т, т.е. в ^невыводимыми являются одновременно формула и ее отрицание.

Т.1. Формализованное исчисление предикатов синтаксически непротиворечиво.

Д-во: Допустим противное, т.е. предположим, что ФИП синтаксически противоречиво. Значит, найдется такая ф-ла F, что F и -iF будут теоремами ФИП. Тогда формулы /и -.Сбудут общезначимыми, что невозможно на основании опр-ия общезначимости. D.

25.Аксиома объемности или аксиома экстенсиональности

утверждает, что множества совпадают в том и только в том случае, если они состоят из одних и тех же элементов.Мн-ва х и у наз-ся различными, если сущ-ет такой z, что zЄх и z неЄу, или же сущ-ет z, что z неЄх и zЄу. Запись: х≠у.

Аксиома пустого множества:

Аксиома суммы, или некоторого объединения

Аксиома множества подмножеств, или аксиома степени:

Аксиома подстановки

Аксиома бесконечности:

[Ø ]

Аксиома фундирования, или аксиома регулярности:

[x≠ Ø ]

Аксиома выбора: если х — дизъюнктное мн-во непустых мн-ств, то сущ-ет такое множество у, к-ое из каждого мн-ва из х содержит точно по одному элементу.

26. Аксиоматическая теория наз-ся непротиворечивой, если ни для какого утверждения А, сформулированного в терминах этой теории, само утверждение А и его отрицание ¬А не могут быть одновременно теоремами этой теории. Если для некоторого утверждения А теории оба утверждения А и ¬А явл-ся ее теоремами, то аксиом-ая теория наз-ся противоречивой.

Т.1. Если акс-ая теория противоречива, а используемая в ней логическая система включает исчисление выск-ий с правилом вывода modus ponens, то любое предложение с этой теорией явл-ся ее теоремой. Док-во: ввиду противоречивости теории существует предложение А теории, такое, что А и ¬А ее теоремы. Тогда сущ-ют их выводы:…,А,…, ¬А. Рассмотрим вывод формулы А→(¬А→C). Применив правило МР к ф-лам ¬А и (¬А→С), получим ф-лу С. Т.о., получается последовательность формул:…,А,…, ¬А,В., А→(¬А→C), (¬А→C), т.е. С – теорема этой теории.

Акс.теория наз-ся категоричной, если любые две ее модели изоморфны.

Аксиома А из системы аксиом ∑ наз-ся независящей от остальных аксиом этой системы, если ее нельзя вывести из множества ∑\{А} всех остальных аксиом системы ∑.

Акс.теория наз-ся полной, если она содержит достаточное для какой-набудь цели кол-во теорем. Акс.теория наз-ся абсолютно полной, если для любого утверждения А, сформулированного в терминах этой теории, точно одно из утверждений А и ¬А явл-ся ее теоремой. Акс.теория наз-ся полной в узком смысле, если добавление к ее аксиомам любого недоказуемого в ней утверждения с сохранением всех правил вывода приводит к противоречивой теории.

Т.2. Всякая абсолютно полная теория будет полна и в узком смысле. Док-во: допустим, что некоторая абсолютно полная теория не полна в узком смысле. Значит, найдется такое утверждение А этой теории, недоказуемое в ней, что новая теория, построенная на основе прежних аксиом и утверждения А в кач-ве новой аксиомы, непротиворечива. А принадлежит новой теории. Ввиду абсолютной полноты исходной теории и недоказуемости в ней утверждения А заключаем, что в ней доказуемо¬А. Поэтому ¬А принадлежит новой теории. Получаем противоречие с тем, что новая теория непротиворечива.

27. Язык логики первого порядка строится на основе сигнатуры, состоящей из множества функциональных символов и множества предикатных символов . С каждым функциональным и предикатным символом связана арность, то есть число возможных аргументов. Допускаются как функциональные так и предикатные символы арности 0. Первые иногда выделяют в отдельное множество констант. Исп-ся след-ие дополнительные символы: символы переменных; пропозициональные связки: ; кванторы: всеобщности и сущ-ия ; служебные символы:(,),,.

Терм есть символ переменной, либо имеет вид , где f — функциональный символ арности n, а  — термы.Атом имеет вид , где р-предикатный символ арности n, а -термы. Формула — это либо атом, либо одна из следующих конструкций: , где F,F₁,F₂ — ф-лы, а x —переменная.

Переменная x наз-ся связанной в ф-ле F, если F имеет вид либо , или же представима в одной из форм , причем x уже связанна в H, F₁ и F₂. Если x не связанна в F, ее называют свободной в F. Ф-лу без свободных переменных наз-ют замкнутой ф-лой, или предложением. Теорией первого порядка называют любое мн-во предлжений.

28. В классическом случае интерпретация формул логики первого порядка задается на модели первого порядка,к-ая опр-ся след-ми данными:1)несущее мн-во D;2)семантическая ф-ия σ,отображающая:- каждый n-арный функциональный символ f из в n-арную ф-ию ;

- каждый n-арный предикатный символ p из в n-арное отношение .

Предположим s-ф-ия, отображающая каждую переменную в нек-ый элемент из D,к-ая наз-ся подстановкой. Интерпретация терма t на отн-но подстановки s задается индуктивно.

- , если х-переменная;

-

В таком же духе опр-ся отн-ие истинности формул на D отн-но s

,тогда и только тогда,когда ;

тогда и только тогда, когда -ложно; ,тогда и только тогда, когда и истинны; ,тогда и только тогда,когда или истинно; ,тогда и только тогда,когда влечет ; , тогда и только тогда,когда для нек-ой подстановки s’, к-ая отличается от s только на перменной х; , тогда и только тогда,когда для всех подстановок s’,к-ые отличается от s только на перенной х.

Формула φ, истинна на , что обозначается как , если , для всех подстановок s. Формула φ называется общезначимой, что обозначается как , если для всех моделей . Формула φ называется выполнимой , если хотябы для одной D.