10. Т.(о дедукции).Если ├f, то т-ма ├ в частности, если ├f, то├ д-во: Предположим,что посл-сть формул (1)

явл-ся выводом ф-лы F из гипотез . Сл-но, ф-ла Bs есть формула G, т.е. Bs = G (= — знак графического совпадения, одинаковости формул).

Рассмотрим посл-сть формул: (2).Эта посл-сть, не является выводом из гипотез . Тем не менее ее можно превратить в такой вывод, если перед каждой ф-лой посл-сти добавить подходящие ф-лы. Для этого покажем методом мат.инд.по l, что

├ . (3) 1) l=1. Покажем, что ├ . Для ф-лы как первого члена посл-сти (1), являющейся выводом F из могут представиться след-щие

возможности: а) есть либо одна из аксиом, либо одна из гипотез . В этом случае вывод формулы из гипотез строится так:

(4).

б) есть гипотеза Fm. Тогда формула Fm→ принимает вид Fm→Fm.

2)l≤к.Предположим, что утверждение (3) верно для всех l≤к и все необходимые выводы добавлены перед всеми k первыми ф-лами посл-сти (2);

3) l= к+ 1, т.е. справедлива выводимость:

├

Для ф-лы как члена посл-сти (1), являющейся

выводом F из гипотез , могут представиться след-щие возможности: а), б) есть либо одна из аксиом, либо одна из гипотез . Данные возможности абсолютно аналогичны

соотв-ющим возможностям из случая l= 1;

в) получена из двух предыдущих формул посл-cти (1) по правилу МР. Сл-но, 1≤i<к+1,1≤j<к+1и ф-ла Bj имеет вид: ,т.е.

Поск-ку 1≤i<к+1,1≤j<к+1, то ф-лы и стоят в посл-сти (2) перед ф-лой и,сл-но,по предположению индукции, справедливы утверждения о том, что имеются выводы этих формул из гипоте .

;

(α+β) ;

(α+β+1) ;

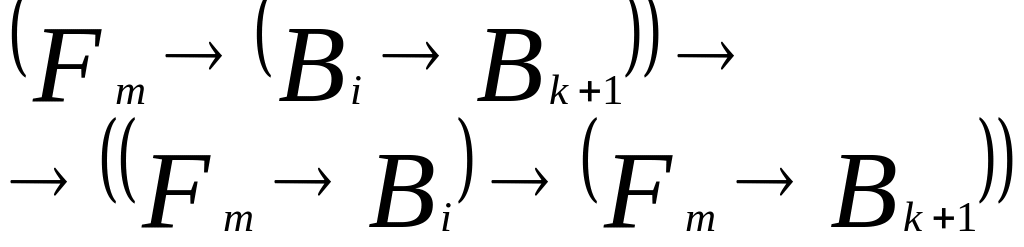(α+β+2) ;

(α+β+3) .

Утверждение (3) верно для любого l=1,2,…,s.При l=s получаем ├

11. Получаемые вторичные

правила вывода носят название производных правил вывода. Разделим их

на две группы и сформулируем их в двух теоремах: в одной —

производные правила введения логических связок, в другой —

производные правила удаления таких связок. Для формулировки правил

будет использоваться символическая запись.

Т.1. (правила введения логических связок).

Справедливы следующие производные правила вывода, называемые правилами введения логических связок (где Г — нек-ое, возможно и пустое,

мн-во формул):

а) введение импликации:

б) введение конъюнкции:

в)введение дизъюнкции:

г) введение отрицания (приведение к абсурду):

Т.2(правила удаления логических связок).

Справедливы следующие производные правила вывода, называемые правилами удаления логических связок (где Г — нек-ое, возможно и пустое,

мн-во формул):

а)удаление импликации :

б)удаление конъюнкции:

в)удаление конъюнкции:

г)удаление дизъюнкции (Генцен):

д)удаление дизъюнкции (Клини):

е)сильное удаление отрицания:

ж)слабое удаление отрицания:

12.Т.(о полноте формализованного исчисления

выск-ий). Ф-ла тогда и только тогда доказуема в формализованном

исчислении выск-ий (явл-ся теоремой исчисления), когда она явл-ся тавтологией алгебры выск-ий.Символически:├F╞F.13.Акс-ская теория наз-ся

непротиворечивой, если ни для какого утверждения А,

сформулированного в терминах этой теории, само утверждение А и его

отрицание ¬А не могут быть одновременно теоремами данной теории.

Если для нек-ого утверждения А теории оба утверждения А и ¬А — теоремы этой теории, то акс-ская теория

наз-ся противоречивой.

Т.(о непротиворечивости формализованного

исчисления выск-ий). Формализованное исчисление выск-ий

есть непротиворечивая аксиоматическая теория.

Д-во.Допустим противное, т.е. предположим, что формализованное исчисление выск-ий противоречиво. Значит, имеется такая ф-ла F, что F и ¬F явл-ся теоремами

формализованного исчисления выск-ий. Каждая из формул F и ¬F явл-ся тавтологией алгебры

выск-ий.Но последнее невозможно на основании

опр-ия тавтологии. Сл-но, формализованное исчисление выск-ий непротиворечиво.

14.Аксиома А из системы аксиом Е наз-ся независящей от остальных аксиом этой системы, если ее нельзя вывести из мн-ва ∑\{А} всех остальных аксиом системы ∑. Система аксиом ∑ наз-ся независимой, если каждая ее аксиома не зависит от остальных.

Л.1. Аксиома (А1) не зависит от остальных аксиом (А2)

и (A3) формализованного исчисления выск-ий.

Л.2. Аксиома (А2) не зависит от аксиом (А1) и (A3) формализованного исчисления выск-ий.

Д-во.Рассмотрим трехэлементное мн-во М = {0, 1, 2}, но операции ¬и → над его элементами

зададим по-другому, с помощью следующих таблиц:

Ф-ла исчисления выск-ий выделенная,если при всякой подстановке вместо ее переменных любых

элементов из М она принимает значение 0. правило вывода МР сохраняет св-во выделенности,т.е. если формулы F и F→G выделенные, то и ф-ла G-выделенная. Сл-но, всякая ф-ла,выводимая из аксиом (А1) и (A3) с помощью правила МР, явл-ся выделенной. Ф-ла (А2) не может быть выведена из аксиом (А1) и (A3) с помощью правила МР, нужно установить, что (А2) не явл-ся выделенной. Действительно, если,

например, F придать значение 0, G — 0 и H— 1, то (А2) примет значение 2.

Л.3.Аксиома (A3) не зависит от остальных аксиом (А1) и (А2) формализованного исчисления выск-ий.

Т.1.Система аксиом(Al), (A2),(A3)формализованного исчисления выск-ий независима.

15. Предикат — предложение, похожее на высказывание, но все же им не являющееся: о нем нельзя судить, истинно оно или ложно.

Определение. Определенным на множествах М1,M2, ..., Мn

n-местным предикатом называется предложение, содержащее n

переменных х1 х2, ..., хn, превращающееся в высказывание при подстановке вместо этих переменных любых конкретных

элементов из множеств М1,М2, ..., Мn соответственно.

Для n-местного предиката будем использовать обозначение Р(х1

x2 ..., хn). Переменные х1,х2 ..., хn называют предметными, а

элементы множеств М1,М2 ..., Мn, которые эти переменные

пробегают, — конкретными предметами. Всякий n-местный предикат Р(х1,х2 ..., хn), определенный на множествах М1,М2 ..., Мn представляет собой функцию n аргументов, заданную на указанных множествах и принимающую значения в множестве всех высказываний. Поэтому предикат называют также

функцией-высказыванием.

Равносильность и следование предикатов. Два

n-местных предиката Р(х1,х2, ..., хn) и Q(x1,x2, ..., хn), заданных

над одними и теми же множествами М1,М2,.., Мn, наз-ся равносильными, если набор предметов (элементов) а1 € Мn, а2 € М2, -.., an € Мn превращает первый предикат в истинное

высказывание Р{а1,а2,..., аn) в том и только в том случае, когда этот

набор предметов превращает второй предикат в истинное

высказывание Q(a1, а2,..., аn).

Другими словами предикаты Р(х1,х2..., хn) и Q(x1,х2,..., хn) равносильны <=> их множества истинности совпадают Р+ =Q+.

записывать: Р<=> Q.

Предикат Q(x1,х2,...,хn), заданный над мн-вами М1,М2,..., Мn, называется следствием предиката Р(х1,х2, ..., хn), заданного над теми же множествами, если он

превращается в истинное высказывание на всех тех наборах значений

предметных переменных из соответствующих множеств, на которых в

истинное высказывание превращается предикат Р(х1,х2, ..., хn.

Другими словами предикат Q является следствием предиката Р <=> Р+ Q+.

записывать : Р => Q.

16. Конъюнкцией двух предикатов P(x) и Q(x) наз-ся новый (сложный) предикат , к-ый принимает значение “истина” при тех и только тех значениях , при к-ых каждый из предикатов принимает значение “истина”, и принимает значение “ложь” во всех остальных случаях.Очевидно, что областью истинности предиката явл-ся общая часть области истинности предикатов P(x) и Q(x), т.е. пересечение .

Дизъюнкцией двух предикатов P(x) и Q(x) называется новый предикат , к-ый принимает значение “ложь” при тех и только тех значениях , при к-ых каждый из предикатов принимает значение “ложь”, и принимает значение “истина” во всех остальных случаях.Ясно, что областью истинности предиката явл-ся объединение области истинности предикатов P(x) и Q(x), т.е. .

Отрицанием предиката P(x) называется новый предикат или , к-ый принимает значение “истина” при всех значениях , при к-ых предикат P(x) принимает значение “ложь”, и принимает значение “ложь” при тех значениях , при к-ых предикат P(x) принимает значение “истина”.Очевидно, что , т.е. мн-во истинности предиката явл-ся дополнением к мн-ву I_P.

Импликацией предикатов P(x) и Q(x) наз-ся новый предикат , к-ый явл-ся ложным при тех и только тех значениях , при которых одновременно P(x) принимает значение “истина”, а Q(x) – значение “ложь”, и принимает значение “истина” во всех остальных случаях. Поскольку при каждом фиксированном справедлива равносильность , то .

Эквиваленцией предикатов P(x) и Q(x) наз-ся новый предикат , к-ый обращается в “истину” при всех тех и только тех , при которых P(x) и Q(x) обращаются оба в истинные или оба в ложные выск-ия. Для его множества истинности имеем: .

17. В логике предикатов будем пользоваться следующей символикой :

1.Символы p, q, r, …- переменные выск-ия, принимающие два значения: 1- истина , 0 – ложь.

2.Предметные переменные – x, y, z, … , к-ые пробегают значения из некоторого мн-ва М;

x⁰, y⁰, z⁰ – предметные константы, т. е. значения предметных переменных.

3.P(·), Q(·), F(·), … - одноместные предикатные переменные;

Q(·,·,…,·), R(·,·, …,·) – n-местные предикатные переменные.

P⁰(·), Q⁰(·,·, …,·) – символы постоянных предикатов.

4.Символы логических операций:

5.Символы кванторных операций:

6.Вспомогательные символы: скобки, запятые.