Теория множеств как средства отображения модели состава.

Теория множеств оперирует  объектами, абстрагируясь от их характеристик только на основе данных о наличии объектов и включении объекта в некоторую совокупность (множество).

 

Множество – это совокупность определенных различных объектов. Упорядоченности элементов во множестве нет.

A={a,b,c,d} =={d,c,a,b}

А – обозначение множества (обычно используются большие буквы латинского или греческого алфавита.

a,b,c,d – элементы множества (обычно используются строчные буквы латинского или греческого алфавита)

{} – знак, указывающий на образование некоторыеми элементами множестваю.

Между элемнтами множества и множеством вцелом существует отношение принадлежности - . Оно указывает на то что данный элемент принадлежит, входит в множество.

a A

– знак принадлежности элемента к множеству.

 Особые типы множеств.

 Ø – пустое множество, т.е. множество, не содержащее элементов.

I – универсум, т.е. множество, содержащее все возможные элементы.

Отношения на множествах.

 

A=A’  - отношение эквивалентности.

Множество А эквивалентно множеству A’, если для любого элемента множества А можно сказать, что он принадлежит множеству A’ и наоборот.

 

A A’ - отношение подмножества.

Множество A является подмножеством множества А’, если для любого элемента множества A можно сказать, что он принадлежит множеству А’, но не наоборот.

* Эквивалентность – частный случай подмножества.

Операции над множествами.

Дополнение.

Д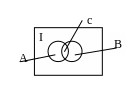 ополнением множества А является множество дополняющее множество А до универсума.

2) Пересечение.

Пересечением множеств А и В является множество элементов одновременно принадлежащих и множеству А и множеству В.

3) Объединение.

Объединением множеств А и В является множество образованное элементами принадлежащими хотя бы одному из исходных множеств.

4) Разность.

Разностью множеств А и В является множество элементов множества А не принадлежащее множеству В.

2. Упорядоченное множество

Упорядоченные множества – это множества, в которых важен порядок элементов.

В упорядоченном множестве могут присутствовать одинаковые элементы, они отличаются своим положением во множестве.

Упорядоченные множества также называют кортежами или очередями.

Упорядоченное множество используется для описания объекта, в котором важен порядок элементов:

• обрабатываемые партии деталей,

• данные об очереди клиентов.

• инструменты в инструментальном магазине станка,

• детали в накопителе станка.

Характеристика кортежа - его длина (количество элементов). В зависимости от длины, кортежи подразделяются на “двойки”, “тройки” и т.д.

Если нет дополнительных требований, то под словом “множество” подразумевается не упорядоченное множество. На упорядоченность множества всегда необходимо указывать.

Упорядоченные и неупорядоченные множества взаимосвязаны. Существуют операции, в которых участвуют два данных типа множеств.

Прямое произведение множеств

C=A´B;

Результатом прямого произведения множеств А и В является множество С, элементами которого являются кортежи образованные всеми возможными сочетаниями элементов множеств А и В. Порядок расположения элементов в кортежах соответствует порядку множеств в прямом произведении.

Например, если А={a,b}, B={x,y,z}, то C=A´B={áa,xñ,áa,yñ,áa,zñ,áb,xñ,áb,yñ,áb,zñ}

Прямое произведение распространяется на n множеств. Результатом прямого произведения n множеств является множество, состоящее из кортежей длиной n. Из понятия прямого произведения следует понятие степени множества. Это произведения множества само на себя.

Для множества являющегося подмножеством результата прямого произведения множеств существует понятие проекции. Результатом проекции множества, являющегося результатом прямого произведения на заданные множества будет множество, элементы которого образованы из элементов множества С удалением из них тех элементов, кортежей которые не входят в множества, на которые производится проекция.

Пусть С=А₁хА₂хА₃хА₄х..хА_n = {áa1 ,a2 , a3, ...anñ/a..A,a..A,a..}.

Пр(С/А,а)={áa,añ/a}