Задача поиска цепи наименьшего веса между двумя вершинами взвешенного графа. Общая постановка задачи.
Задача решается при анализе структуры с многими дополнительными связями, т.е. вариантов соединения двух вершин существует несколько или в общем случае некоторое множество. При этом возникает задача выбрать вариант обеспечивающий минимальный расход ресурсов при соединении вершин N1 и N2.
Дано:
G=<V, U> - взвешенный граф
T(N×M) – взвешенная матрица смежности
N1 – начальная вершина
N2 – конечная вершина
Найти: цепь соединяющую N1 и N2 и имеющую наименьший суммарный вес дуг по сравнению с другими вариантами.
Методы решения задачи.
Приближённые методы дают решения отличающееся от действительно оптимального, но обычно их трудоёмкость меньше чем методов дающих точное решение.
Метод ближайшего соседа (БС).
В цепь включается вершина ближайшая к последней включенной, пока не будет достигнута вершина N2. Если возникает тупик, то происходит отступление на один шаг назад по цепи.
Может рассматриваться как модифицированный поиск в глубину. В качестве смежной вершины берётся не любая, а связанная дугой наименьшего веса.
Достоинство данного метода – простота и очевидность. Недостаток – большая неточность.
Точные методы, дают действительно оптимальное решение, но обычно очень трудоёмки.
Метод полного перебора.
Формируются все возможные решения (все варианты цепей соединяющих N1 и N2) вычисляются их суммарный вес, и выбирается цепь с минимальным весом.
Данный метод точен, однако довольно трудоемок.
I)Метод направленного поиска (динамического программирования) он же алгоритм Дейкстры. (Дайкстры)
Данный алгоритм представляет собой пошаговый пересчет веса цепей от начальной вершины S до всех остальных вершин графа. Отдельный шаг алгоритма включает вычисление новых весов цепей от S-й вершины до каждой Vj и сравнение вычисленных весов с весами цепей между этими же вершинами, принятыми на предшествующих шагах.
Для дальнейшего рассмотрения в качестве цепи до вершины Vj оставляется цепь с наименьшим весом. Таким образом в конце алгоритма выявляются цепи наименьшего веса до всех вершин графа.
Новый вес цепи до вершины Vj на каждом шаге вычисляется как сумма веса цепи от вершины S до вершины ближайшей к ней на предшествующем шаге, и дуги от вершины ближайшей к S на предшествующем шаге до вершины Vj. . Таким образом, общая формула пересчёта веса цепи от вершины S до вершины Vj имеет вид
,
(1*)
где
L(I,Vj) – вес цепи от вершины S до вершины Vj найденное на i-ом шаге.
L(I-1,Vj) – вес цепи от вершины S до вершины Vj найденное на предыдущем шаге.
L(I-1,U) – вес цепи от вершины S до вершины ближайшей к ней на I-1 шаге.
T(U,Vj) – вес дуги от вершины ближайшей к S на I-1 шаге до вершины Vj
Вершина, которая оказалась к S ближайшей на каком либо шаге из дальнейшего рассмотрения исключается: до неё уже найдено кратчайшее расстояние.
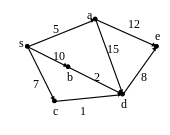
Пусть задан граф G
N1=S
N2=e
На нулевом шаге в качестве весов цепей (L) от вершины S до всех вершин Vj принимается значение бесконечность, кроме вершины S.
-
0
1
2
3
4
5
S
0
0
0
0
0
0
a
∞
5
5
5
5
5
b
∞
10
10
10
10
1
0c
∞
7
7
7
7
7
d
∞
∞
20
8
8
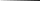
8
e
∞
∞
17
1
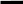71
616
Рис 4.13. Заданный граф и этапы Алгоритма направленного поиска.
Алгоритм направленного поиска разбивается на 2 части:
Прямой ход
Обратный ход
При прямом ходе рассчитываются минимальный вес цепей до всех вершин графа от начальной вершины S. При обратном ходе, т.е. второй части алгоритма, выявляются состав цепей,.
При обратном ходе, необходимо последовательно проследить, относительно какой вершины найдено последнее значение веса цепи до конечной вершины. Затем необходимо проследить, относительно какой вершины найдены цепи до выявленной вершины и т.д. до начальной вершины.
Прямой ход алгоритма направленного поиска.
Этап 0.
Все вершины графа помещаются в множество И – множество исходных вершин.
II={a,b,c,d,e}
Устанавливается номер шага I=0
В качестве исходных весов цепей от начальной вершины S, до всех вершин графа заносится в бесконечность (), кроме самой вершины S. Для нее устанавливается значение 0.
В качестве вершины U, т.е. вершины ближайшей к S принимается сама вершина S.
Вершина U вычеркивается из множества вершин II.
Этап 1.
Устанавливается следующий номер шага. Пересчитываются веса цепей от вершины S до всех вершин множества II по формуле ( *1):
Этап 2.
Выбирается вершина ближайшая к S на I-ом шаге, т.е. вершина с минимальным значением L(I,Vj). Данная вершина принимается в качестве вершины U на I-ом шаге.
Вершина U вычеркивается из множества II.
Этап 3.
Если все вершины из множества II вычеркнуты, то конец прямого хода и переход к обратному ходу. Иначе переход к этапу 1.
Если в графе нет дуг с отрицательным весом, то прямой ход можно заканчивать когда в качестве вершины U будет принята вершина N2.
Задача поиска варианта обхода всех элементов системы с наименьшей затратой ресурсов. Задача коммивояжера.
Общая постановка
Задача коммивояжера (почему? Пояснить)
задача поиска минимального гамильтонова цикла).
Гамильтонов цикл – это цикл, который включает все вершины графа. В общем случае граф может не содержать гамильтоновых циклов, или с другой стороны гамильтоновых циклов может быть некоторое множество. Необходимым условием существования гамильтоновых циклов является отсутствие «висящих» вершин в графе. Есть другие необходимые условия существования гамильтоновых циклов..
Задача коммивояжера решается как транспортная задача, то есть когда требуется соединить все элементы системы одним циклом, не повторив ни один элемент. Также данная задача возникает в задачах планирования, как поиск последовательности выполнения работ, при известных затратах связанных с переключением с одной работы на другую.
Например, требуется выполнить некоторое множество работ на одном рабочем месте, причем при переходе от одной работы к другой необходимо переналаживать рабочее место, при этом для каждой пары работ время переналадки различное, то есть возникает задача выбора такой последовательности выполнения работ, при котором суммарное время переналадки будет минимальным.