Фазовый метод:фазов простр-во,построен-е троекторий.
Основ-н на представ-ии о фазов простр-ве и представ-м динамики сист дв-ием точки в это простр-во.
В
прост случае сист однокоординатная:
Для того чтобы знать как сист поведёт себя в будущ необход знать:
Полн опис-е сист-опис-е вых сигнала и n производных.
Постр n-мерное простр-во и сост-е сист в точку в этом n+-мерном простр-ве (двиг-ся только по непрерыв кривой).
Исследуя св-ва кривой(длину,кривизну) можно много узнать о повед-ие сист.
n=2
Фаз траектория имеет направ-ие,т.к это послед отсчёты во времени.У люб траектории сущ-т определ правила:
1)в верх полупл-ти траектор может идти только слева-направо.В нижн-справа налево.
2)ось абсцисс может пересек только под прям углом.
3)сколь бы не сложна была троект-ия,будучи опред-ой для одной и той же сист при одних и тех же усл-ях троект-ия не может пересечь сама себя.Если это произошло знач проекция троект-ии в фаз простр-ве(не все пар-ры сист истены, она не изучена).
Прост-во больш разм-ти услож-ет постр-ие траектории.
В этих случ-х точка будет устойч фокусом.
Траектор могут иметь узлы-устойч и неустойч.Узлы получ-ся в периодич движ-ии.
Фокусы получ-ся в периодич движ-ии.
Применение метода фазовых траекторий для анализа устойчивости систем управления.
Основан на представл. о фазовом простр-ве и предст-нием динамики системы движ-нием точки в это простр-во.
В простом случ. сис-ма однокоорд.
x=x(t);
Для того, чтобы
знать как сис-ма поведёт себя в будущем,
необх. знать:
n=2,
-это
фазов. траек-рия.
Фаз. траектория имеет направл., т.к. это последн. отсчёты во времени. У иной траектории сущ. правила (аксиомы):
1. В верхн. полуплоск-сти траект. может идти только слева - направо.
В нижней только справа – налево.
2. Ось абсцисс может пересекаться только под прямым углом.
3. Сколь бы не сложна была траектория, будучи определённой для одной и той же сис-мы при одних и тех же условиях, траектория не может пересечь сама себя. Если это прошло, значит это проекция траектории в фазовом пространстве.
Траектории могут иметь узлы – устойчивые и неустойчивые. Узлы получаются в непериодич. (апериод.) движ-нии.
Фокусы получ. в периодич. дв-нии.
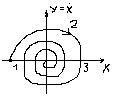
т. (0;0) – явл. устойч. узлом.
Цикл – замкн., фаз. траектория.
Предельный цикл:
Устойчивый
Неустойчивый
If некоторая траектория явл. устойч. циклом, то траектория, находящ. вне её, должны скручиваться к этому циклу, а затем двигаться по циклу.
If точка нах. внутри, then траектория должна раскручиваться до предельного цикла.
Пред. цикл явл. притягивающейся траекторией (аттрактором).
Устойчивый пред. цикл опред. устойч. автоколебания в системе.
Это св-во сис-мы, по сути, внутри саморегулирования.
Неустойч. пред. цикл – такая траектория, что любое отклонение в сторону меньших амплитуд приведёт к скручиванию колебаний; в сторону больших амплитуд – раскручивание.
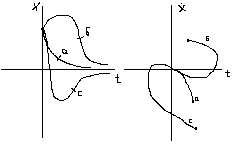
Методика построения фаз. траекторий:
I способ: графо – аналитический.
If сущ. эксперем. получ. график вых. процесса, then для равноотстоящих промежутков времени в соотв. т. графика нах. координату и производную.
II способ: аналитический (матем.)
Поскольку траектория – ф-ция 2-х координат, то надо попытаться изв. ДУ преобразовать так чтобы:
Затем найти зависимость y=f(x), исключить t.