31. Функциональные комплексные ряды

Функциональным комплексным рядом называется ряд

где - комплексные функции комплексного переменного, заданные на некотором множестве Е комплексных чисел. В дальнейшем комплексные функции комплексного переменного будем называть комплексными функциями). Сумма называется частичной суммой ряда (6.16).

Определение 6.4.

Комплексный функциональный ряд называется сходящимся в точке множества , если сходится следующий числовой комплексный ряд

(6.17)

где - числа - значения функций в точке .

Определение 6.5.

Функциональный комплексный ряд (6.16) называется сходящимся к функции на множестве Е если он сходится в каждой точке и сумма этого ряда в произвольной точке равна .

Пример 1.

Рассмотрим ряд

(6.18)

который в дальнейшем будем называть геометрическим рядом. Здесь - функции заданные на всем множестве комплексных чисел .

(6.19)

Очевидно вспомогательное тождество

(6.20)

(Тождество хорошо известно для . Используя метод матиндукции, его можно доказать для любого ).

Из (6.20) имеем

Откуда на основании (6.19) имеем

Пусть - любое комплексное число. При функциональный комплексный ряд (6.18) превращается в комплексный числовой ряд

(6.22)

Частичная сумма последнего ряда на основании (6.21) имеет вид

(6.23)

Из (6.23) следует

(6.24)

Отсюда видно, что если , то

при

А это значит, что

при

т.е.

(6.26)

Поскольку - любое комплексное число, модуль которого меньше 1, то мы доказали, что функциональный ряд (6.18) сходится в круге (рис.6.1) к функции которая в этом случае и является суммой функционального ряда в круге .

Очевидно, при -й член ряда (6.18) не стремится к нулю, необходимый признак

сходимости ряда не выполняется, и при ряд (6.18) расходится.

Определение 6.6.

Функциональный ряд (6.16) называется равномерно сходящимся к своей сумме на множестве , если для любого существует , что для всех и всех выполняется неравенство .

Обозначив определение равномерной сходимости ряда (6.16) можно сформулировать так: функциональный ряд называется равномерно сходящимся к своей сумме на множестве , если для любого существует , что для всех и всех выполняется неравенство

Укажем важный для приложений достаточный признак равномерной сходимости.

Теорема 6.3.

Если числовой положительный ряд

сходится и для всех

то функциональный комплексный ряд равномерно сходимся на множестве .

Доказательство.

Так как ряд сходится, то для любого существует такой номер , что при . Из неравенства и сходимости числового положительного ряда имеем, что функциональный ряд сходится абсолютно в каждой точке множества . Учитывая, что при всех , получим

для любого и любого , что и доказывает равномерную сходимость ряда на множестве .

Пример 2.

Покажем, что ряд (6.18) равномерно сходится во всяком круге .

Рассмотрим числовой положительный ряд

где (6.27)

Ряд (6.27) представляет собой геометрическую прогрессию и сходится при 1. В круге имеем

(6.28)

при

По теореме (6.3) в силу (6.28) ряд (6.18) равномерно сходится в круге .

Замечание 1.

Следует заметить, что в круге ряд сходится, но неравномерно. В самом деле,

мы знаем, что в круге ряд (6.18) сходится к сумме , т.е

Имеем также

Отсюда видно, что для любого мы не можем добиться выполнения неравенства

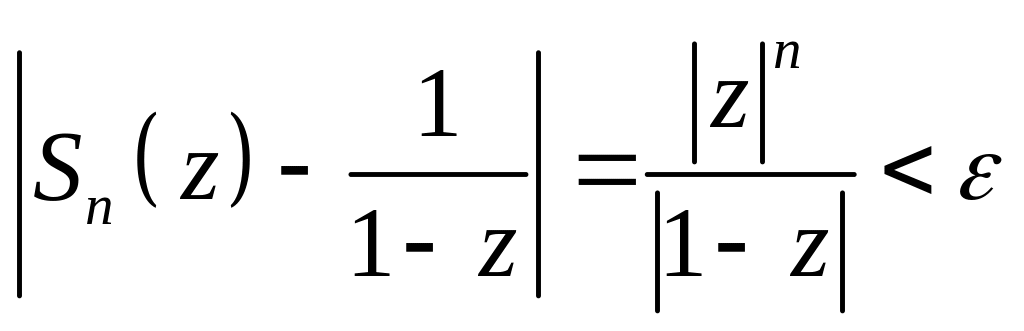(6.29)

для всех из круга , одновременно, ибо при

а значит при т.е. и неравенство (6.29) невозможно для всех из круга одновременно.

Также, как и для действительных рядов доказываются следующие две теоремы. Теорема 6.4.

Если функциональный комплексный ряд составлен из функций непрерывных на множестве и равномерно сходится на этом множестве, то и сумма ряда

будет функцией непрерывной на множестве .

Доказательство.

Пусть - произвольная точка множества докажем непрерывность суммы ряда в этой точке.

Возьмем произвольное число . Так как функциональный ряд равномерно сходится на множестве , то можно найти такой номер , что для всех и всех выполняется неравенство

где

Зафиксируем теперь какой-нибудь номер и рассмотрим частичную сумму ряда с этим фиксированным номером.

Так как непрерывна в точке , то для числа можно найти такое , что для всех , удовлетворяющих условию выполняется неравенство

Теперь для разности получим

для всех , удовлетворяющих условию

Таким образом, мы доказали, что для любого можно найти такое , что для 2, удовлетворяющих условию , выполняется неравенство

Непрерывность в произвольной точке доказана. Этим самым доказана ее непрерывность и на множестве .

Теорема 6.5.

Если составленный из непрерывных функций ряд равномерно сходится в области к сумме то этот ряд можно интегрировать почленно по любой спрямляемой дуге , целиком расположенной в области , т.е.

(6.80)

Доказательство.

Интеграл имеет смысл, так как, по теореме 6.4. непрерывна в .

Так как ряд сходится равномерно в области , то для любого заданного можно указать такой номер что для всех

при

где - длина дуги , a Тогда

что и доказывает теорему.

Пример 3.

(6.31)

Пусть произвольная кривая принадлежащая кругу (рис. 6.2). Функции - непрерывные на всей комплексной плоскости, а значит, и на кривой .

Следовательно,

В предыдущей теореме было отмечено, что при определенных условиях комплексные функциональные ряды можно почленно интегрировать. Возникает вопрос: при каких условиях можно комплексный ряд дифференцировать? Ответ на это вопрос дает следующая теорема.

Теорема 6.6 (Вейерштрасса).

Если функциональный ряд

составлен из функций аналитических в области и равномерно сходится во всяком замкнутом круге , то сумма ряда есть функция аналитическая в области и ряд можно почленно дифференцировать любое число раз, т.е. для любого , имеем

(6.32)

(6.33)

Доказательство.

1. Докажем, что при условиях теоремы сумма ряда есть функция аналитическая в области . Пусть - любая точка из области . Построим круг с центром в точке . Пусть - любая спрямляемая замкнутая кривая, которая принадлежит круг (рис.6.3).

По условию теоремы ряд (6.33) равномерно сходится в круге и составлен из аналитических, а значит, непрерывных в области функций.

Тогда по теореме 6.4 сумма ряда есть функция непрерывная, а по теореме 6.5 ряд можно почленно интегрировать по любой замкнутой кривой , т.е.

По теореме Коши для односвязной области имеем :

(6.35)

при

Из (6.34) и (6.35) имеем

(6.36)

для любой замкнутой кривой . Из (6.36) на основании теоремы Морера следует, что в круге функция есть функция аналитическая, а значит в точке функция дифференцируема. Поскольку - произвольная точка из области , то мы получили, что функция дифференцируема в каждой точке области, а это означает аналитичность функции в области .

Первая часть теоремы доказана.

2. Разделим левую и правую части равенства (6.33) и получим

ряд (6.37) в силу равномерной сходимости ряда (6.33) в замкнутом круге будет равномерно сходится на окружности ограничивающей этот круг. Следовательно, по теореме 6.5 ряд (6.37) можно почленно проинтегрировать по кривой .

(6.38)

На основании интегральных формул для производных т-то порядка (см. параграф "Бесконечная дифференцируемость аналитических функций") из (6.38) получим

(6.39)

Так как - произвольная точка области , то из (6.39) мы получили, что в каждой точке области ряд (6.33) можно почленно дифференцировать любое число раз.

Теорема доказана.