1. Комплексные числа

Рассмотрим множество всех действительных чисел и поле действительных чисел. Первое обозначим символом , второе символом . Пусть, далее — декартово произведение на себя. Другими словами — это множество всех упорядоченных пар , где и .

Два элемента и множества считаются равными тогда и только тогда, когда

, .

Определим на алгебраические операции сложения и умножения следующим образом.

Суммой элементов и на­зывается элемент , а произведением элемент .

Непосредственно из определений следует, что введенные операции коммутативны: , .

Для произвольных элементов справедливы равенства , т.е. выполняется закон ассоциативности соответственно по отноше­нию к сложению и умножению. Проверка показывает, что эти операции подчинены закону дистрибутивности

.

Вычитание определяется как операция, обратная сложению, т.е. разностью называется элемент , обладающий свойством .

Если , , то .

Деление определяется как операция, обратная умножению, т.е. под частным , , пони­мается элемент , обладающий свойством . Последнее равенство равносильно системе

для которой определитель равен и, следовательно, система имеет единственное решение, определяемое формулами

; .

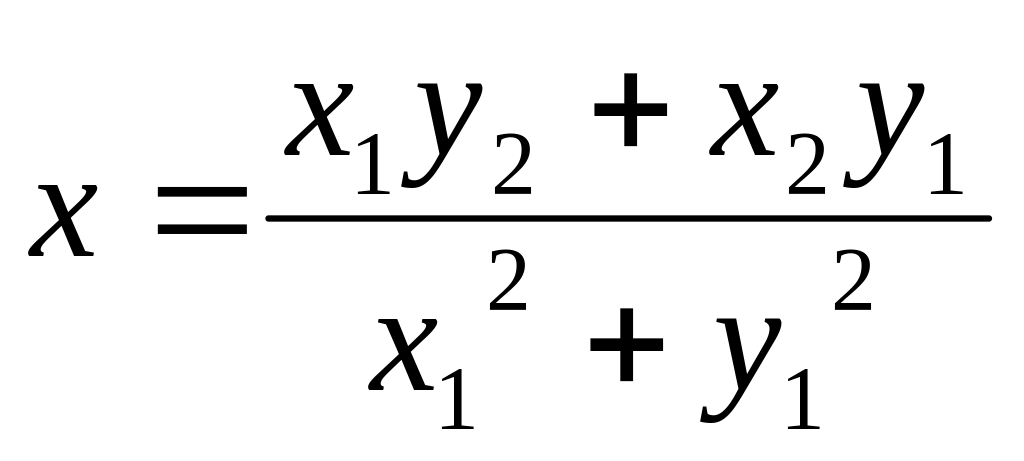Итак, частное от деления на определяется равенством

.

Рассматриваемое множество упорядоченных пар с введенными операциями сложения и умножения представляет собой, как видим, поле. Оно называется полом комплексных чисел и обозначается символом . Элементы поля называются комплексными числами. Роль единицы поля выполняет комплексное число . Действительно, для любого комплексного числа имеем . Множество всех комплексных чисел вида образует подполе поля . При этом изоморфно полю действительных чисел, т.е. между элементами полей и . можно установить взаимно однозначное соответствие, сохраняющееся при операциях сложения и умножения, а значит, вычитания и деления.

Ввиду изоморфизма и естественно, когда речь идет лишь об алгебраической структуре, отождествлять поля и , отождествляя соответствующие друг другу элементы и разных полей. Это дает основание вместо писать , т.е. .

Например, .

Для обозначения упорядоченной пары вводится символ , который будем называть мнимой единицей. Заметим, что или, что тоже .

С помощью символа комплексное число может быть представлено в алгебраической форме

.

Исходя из этой записи, число называют действительной, а число – мнимой частью комплексного числа и пишут

,

(Realis – действительный, Jmaginaris – мнимый).

Комплексное число называется сопряженным с комплексным числом .

Обозначение: .

Легко проверяются следующие равенства:

; ;

; .

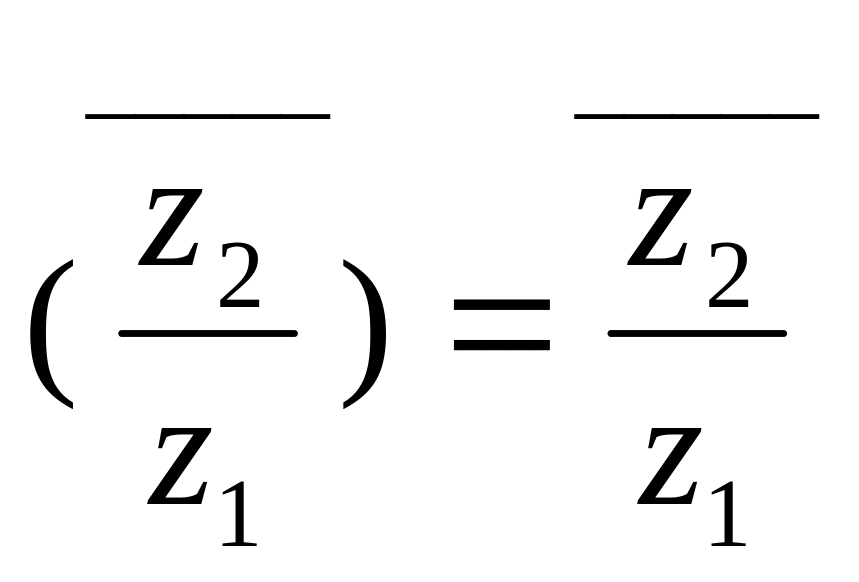2. Геометрическая интерпретация комплексных чисел и основных операций над ними

П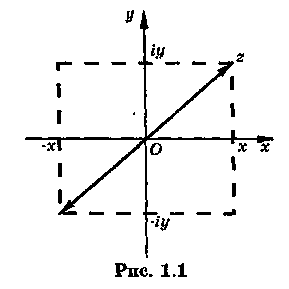 усть на плоскости задана прямоугольная система координат. Комплексное число изображается точкой плос­кости с координатами и эта точка также обозначается буквой (рис. 1.1). Такое соответствие между комплексными числами и точками плоскости, очевидно, является взаимно однозначным. При этом комплексные числа изображаются точками оси абсцисс. Поэтому ось абсцисс называется действительной осью.

Чисто мнимые числа изображаются точками оси ординат, поэтому эта ось называется мнимой осью.

Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью.

Каждому комплексному числу соответствует также вектор с координатами . Если начало вектора брать в начале координат, то соответствие между комплексными числами и векторами с началом в начале координат будет взаимнооднозначным. Вектор, соответствующий комплексному числу , также будем обозначать буквой .

Определение 1.1.

Число называется модулем комплексного числа и обозначается через

.

Очевидно, , причем тогда и только тогда, когда .

Отметим две формулы

, ,

которые непосредственно вытекают из определения модуля комплексного число. Из определения модуля комплексного числа и рис. 1.1. видно, что длина вектора равна и имеют место неравенствам

, .

Е сли , то, как мы знаем, по определению , а это означает, что комплексному числу соответствует вектор равный сумме векторов и (рис. 1.2).

Из рис. 1.2 видно, что разности соответствует вектор , а расстояние между точками и равно длине вектора , т.е. равно .

Кроме этого, легко заметить, что наряду с вектором разности комплексных чисел соответствует вектор , который можно отождествлять с вектором , ибо эти два вектора одинаково направлены и имеют одинаковые модули.

,

т.е. расстояние между точками и равно .

О пределение 1.2.

Аргументом комплексного числа называется угол между положительным направлением оси абсцисс и вектором . При этом, если отчет ведется от оси против часовой стрелки, то величина угла считается положительной, а если по часовой стрелке — отрицательной. Аргумент обозначается так: (рис.1.3). Для числа аргумент не определяется. Очевидно, что аргумент комплексного числа определяется с точностью до чисел вида

, .

В самом деле, если — аргумент комплексного числа, то, как видно из рис. 1.3, аргументом будет также любой из углов

, .

Определение 1.3.

Единственное значение аргумента комплексного числа , удовлетворяющее условию , называется главным значением аргумента и обозначается .

Для главного значения аргумента справедливы соотношения:

, если ;

, если , ;

, если , ;

, если , ;

, если , .

Из рис. 1.2 видно, что равен углу между положительным направлением оси абсцисс и вектором или, что тоже самое, равен углу между положительным направлением оси абсцисс и вектором с началом в точке , с концом в точке .

Пример 1.

Множество точек , удовлетворяющих уравнению , есть окружность радиуса с центром в точке , так как — расстояние между точками и .

Неравенства треугольника. Для любых комплексных чисел и имеют место неравенства

. (1.1)

Доказательство.

Длины сторон треугольника с вершинами в точках , , равны , и (См. рис. 1.2).

Следовательно, неравенства (1.1) являются известными из элементарной геометрии неравенствами для длин сторон треугольника.