
- •§1. Цилиндрические и канонические поверхности.
- •§2. Поверхности вращения
- •§3. Общее уравнение пов. II-го порядка. Привидение общего ур. Пов. II-го порядка к простейшим уравнениям пов. II-го порядка.
- •§8. Конус 2-го порядка.
- •§9. Эллиптический параболоид.
- •§5.Эллипсоид
- •§6.Однополосный гиперболоид
- •§7.Двуполостной гиперболоид
- •§10. Гиперболический параболоид.
- •§11.Цылиндры второго порядка
- •§12 .Перетин поверхні другого пор. З прямою. Асимптотичні напрямкию.
- •§15. Визначення кононічного рівняння поверхні по ортогональним інваріантам
- •§4.Поверхности, которые определяются общим уравнением поверхности второго порядка.
- •§14. Центр поверхности 2го порядка. Классификация поверхности по характеру места их центра.
- •§13 Касательна плоскость и нормаль к пов. Второго пор
§12 .Перетин поверхні другого пор. З прямою. Асимптотичні напрямкию.
Асимптотичний конус. Конус асимптотично напрямлений
Припустимо що відносно ПДСК поверхня 2-го пор. задана загальним рівнянням
Розглянемоперетин з прямою
![]() (2)
(2)
![]() -напрямний
-напрямний
![]() підставимо
в рівняння поверхні вираз (2) та згрупуємо
подібні
підставимо
в рівняння поверхні вираз (2) та згрупуємо
подібні
![]() (3)
(3)
![]()
![]()
![]()
Вирішивши (3) ми отримаємо координати точки перетину підставимо знайдені значення t в (2)
При цьому можливі наступні випадки
1)![]() (7)(напрямний
вектор
називається
асимптотичним напрямком відносно
поверхні (1) якщо він задовольняє рівняння
(7)
(7)(напрямний
вектор
називається
асимптотичним напрямком відносно
поверхні (1) якщо він задовольняє рівняння
(7)
Очевидно в цьму випадку пряма або перетинає поверхню в одній точці
a)

б)![]() -не
перетинаэ
-не
перетинаэ
в)
![]() -є
нескінченне число рішень, а значить
пряма належить повершні
-є
нескінченне число рішень, а значить
пряма належить повершні
Рівняння
![]() (8)є
однорідним, то воно визначаєв просторі
конічну повершню утворену прямими, що
проходять через початок координат і
координати точки M
що лежить на твірній конуса є координатами
вектора
(8)є
однорідним, то воно визначаєв просторі
конічну повершню утворену прямими, що
проходять через початок координат і
координати точки M
що лежить на твірній конуса є координатами
вектора
![]()
Відповілно твірні конуса (8)- це прямі що мають асимптотичний напрямок поверхні справедливе і обернене
Конусом асимптотичних напрямків – наз ГМТ прямих, що проходять через точку M і мають відносно пов. Асимптотичний напрямок Рівнянн цього конуса має вигляд

Конус асимптотитчно напрямлений отримується із асимптотичного конуса паралельним переносом
2)
![]()
- два кореня які співпадають
![]()
![]() в
даному випадку маємо дві точки з дійсними
чи умовними координатами
в
даному випадку маємо дві точки з дійсними
чи умовними координатами
![]() точка
M
назив.
Особливою точкою поверхні якщо
точка
M
назив.
Особливою точкою поверхні якщо
![]()
Якщо хоча б одна з часткових похідних в точці M не дор. 0 то така точка наз. особливою.
§15. Визначення кононічного рівняння поверхні по ортогональним інваріантам
Розглянемо пов. 2-го роду задану відносно ОДСК
Рівнянням (1) Введемо наступні позначення
![]()



Можемо переконатися що даний вираз є ортогональним інваріантом
Для випадку поверхні яка має пряму центрів інваріантом буде
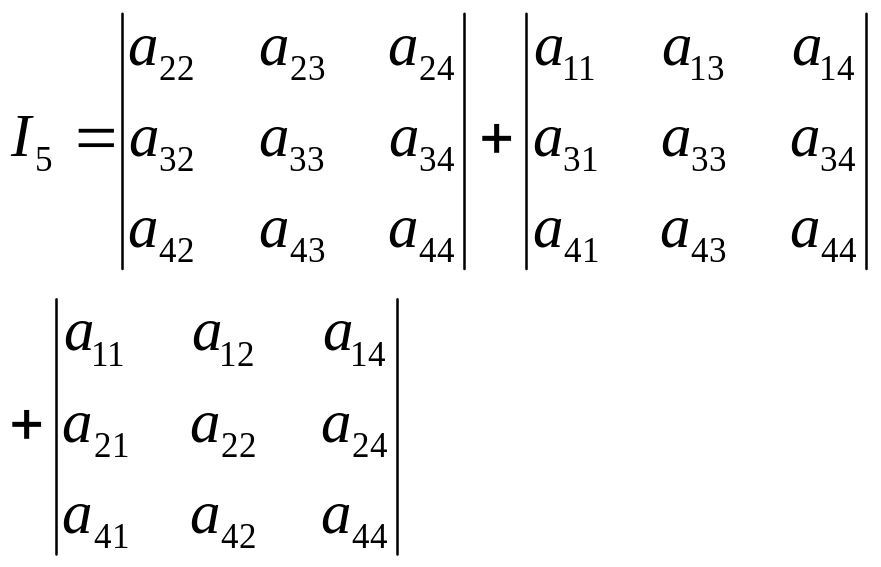
Якщо поверхня має площину центрів
То для неї орт. Інваріантом буде
![]()
§4.Поверхности, которые определяются общим уравнением поверхности второго порядка.
Т - ма: Общее уравнение поверхности второго порядка
Заданной относительно ОДСК выражает одну из следующих 17 поверхностей:
група |
Каноническое уравнение |
Название |
|
I |
1 |
|
Элипсоид |
2 |
|
Мнимый элипсоид |
|
3 |
|
Однополосный гиперболоид |
|
4 |
|
Двуполосный гиперболоид |
|
5 |
|
Конус |
|
6 |
|
Мнимый конус |
|
II |
7 |
|
Эллиптический параболоид |
8 |
|
Гиперболический параболоид |
|
III |
9 |
|
Элептический цилиндр |
10 |
|
Мнимый Эллиптический цилиндр |
|
11 |
|
2 мнимых пересек. плоскости |
|
12 |
|
Гиперболический цилиндр |
|
13 |
|
Пересек. плоскости |
|
IV |
14 |
|
Параболический цилиндр |
V |
15 |
|
2 паралельные плоскости |
16 |
|
2 мнимые паралельные плоскости |
|
17 |
|
2 совпадающие плоскости |
|
Док: уравнение (1) может быть сведено к одному из следующих 5 простейших:
I.
![]()
1) Пусть в (I)
![]() одного знака, а D
им имеет знак противоположнынй.
одного знака, а D
им имеет знак противоположнынй.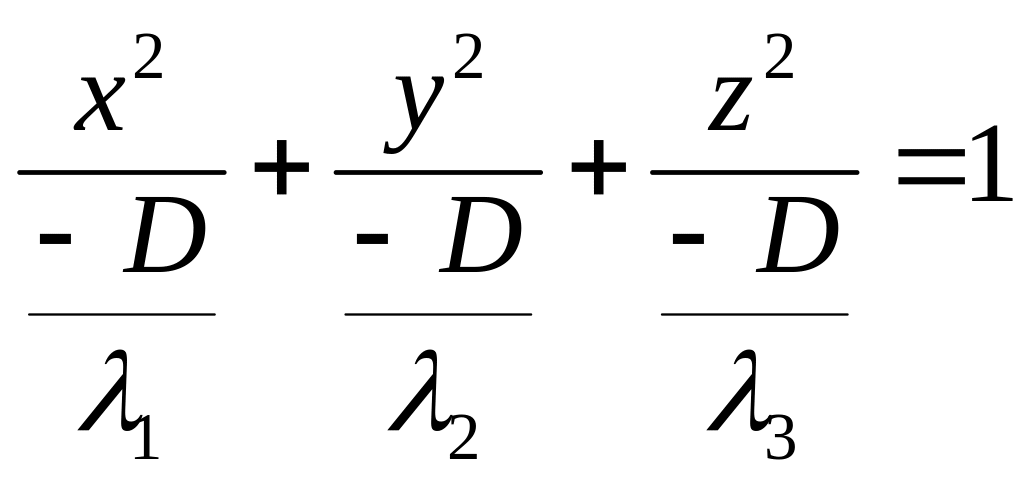
То получим уравнение эллипсоида.
2)
и D
имеют один знак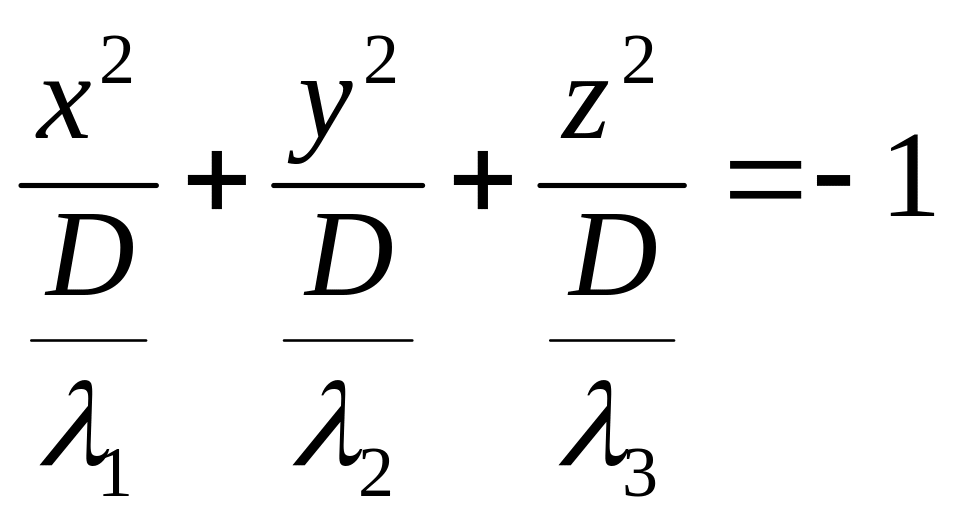 Мнимый
эллипсоид.
Мнимый
эллипсоид.
3)
![]() один
знак, а
один
знак, а
![]() потивоположный.
потивоположный.

Однополосный гиперболоид.
4)
![]() ,
,![]() одного, а
одного, а![]() противоположного.
противоположного.

Двопол. Гиперболоид.
5)D = 0 одного знака,а потивоположного.
![]() Уравн.
Конуса.
Уравн.
Конуса.
6) D
= 0
одного
знака
![]() Мнимый
конус.
Мнимый
конус.
(II)
![]()
7)
одного
знака
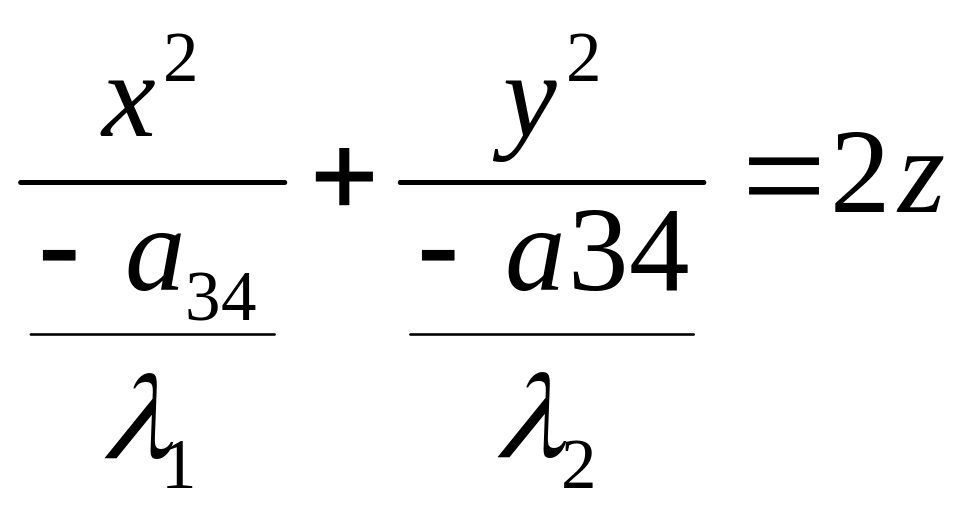
![]() p
и q
будут одного знака (выбираем положительное
направление оси OZ
можна добится того, чтобы знак
p
и q
будут одного знака (выбираем положительное
направление оси OZ
можна добится того, чтобы знак
![]() был противлположным знаку
тогда
p
и q
> 0) мы получим каноническое уравнение
эллиптического параболоида.
был противлположным знаку
тогда
p
и q
> 0) мы получим каноническое уравнение
эллиптического параболоида.
Аналогично моно рассмотреть простейшее уравнение для III, IV, V групп.


