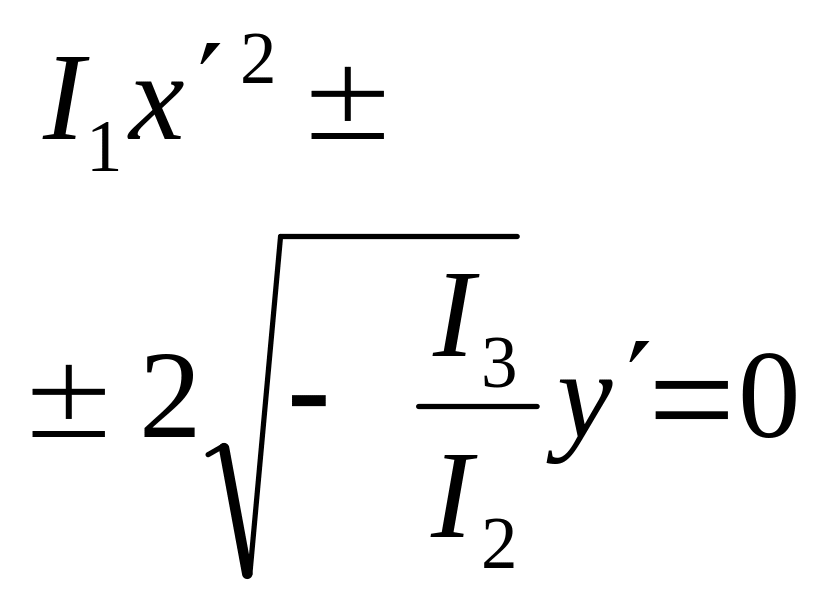- •§1. Общее уравнение линий второго порядка. Приведение общего уравнения к простейшим уравнениям линий второго порядка
- •§2. Линии, определяемые общим уравнением линий второго порядка.
- •§3. Эллипс и его каноническое уравнение
- •§4.Исследования формы эллипса. Эксцентриситет эллипса.
- •§5.Директрисы эллипса и их свойства.
- •§6. Эллипс, как образ окружности при равномерном сжатии его диаметра. Параметрическое уравнение Эллипса
- •§7. Исследование форм гиперболы
- •§8. Исследование форм гиперболы.
- •§9. Эксцентриситет и директрисы гиперболы.
- •§10. Параметрическое уравнение гиперболы. Сопряжённые гиперболы
- •§11.Парабола и ее каноническое уравнение
- •§12.Общие определения эллипса, гиперболы и параболы через эксцентриситет.
- •§13.Полярное уравнение эллипса, гиперболы и параболы.
- •§14. Взаимное расположение прямой и линии 2го порядка. Асимптотическое направление. Классификация линий 2го порядка по их асимптотическим направлениям.
- •§15. Касательная и нормаль линии 2го порядка, их уравнения.
- •§16. Оптические свойства линий 2го порядка.
- •§17 Центр линий 2го порядка. Их классификация по характеру места центров.
- •§18 Диаметр, сопряженный данному неасимтотическому направлению. Сопряженные направления и диаметры. Особые и неособые направления.
- •§19 Главное направленние. Главный диаметр.
- •§20. Уравнение линий второго порядка, отнесенное к двум ее сопряженным диаметрам.
- •§21. Уравнение линий второго порядка в одск, если направление осей является главными.
- •§22.Определение канонического уравнения линии 2-го порядка при помощи ортогональных инвариантов.
- •§23. Таблица для определения вида линии 2-го порядка по ортогональным инвариантам.
- •§24. Построение центральной линии 2-го порядка заданной общим у-нием.
- •§27.Побудова лінії 2 порядку, як канонічний перетин.
§22.Определение канонического уравнения линии 2-го порядка при помощи ортогональных инвариантов.
Т-ма1:Для того, чтобы
линия 2-го порядка, задана общим
уравнениемВида![]() (1) относительно
ПДСК, относилась к I группе чтоб I2 0;к
II группе чтоб I2=0, I3 0; к III группе чтоб
I2= I3=0, I1 0.
(1) относительно
ПДСК, относилась к I группе чтоб I2 0;к
II группе чтоб I2=0, I3 0; к III группе чтоб
I2= I3=0, I1 0.
Доказ: Пусть линия задана уравнением (1),тогда при помощи перехода к новой ПДСК это уравнение может быть приведено к одному из следующих 3-х видов:
I.![]() (2)
(2)
I2=
![]()
II.![]() (3)
(3)
I2=![]() ;
;
I3=

III.
![]() (4)
(4)
I2=
![]() ;
;
I3=

I1=a11≠0
![]() Метод от
противного.Пусть I2
Метод от
противного.Пусть I2![]()
Теорема 2:Если линия 2-го порядка задана относительно ПДСК уравнением вида (1), то ее каноническое уравнение (простейшее) уравнение в зависимости от принадлежности к группе имеет вид:
I.
![]() (6)
(6)
II.
![]() (7)
(7)
III.
![]() (8)
(8)
Где
![]() -корни
характери стического уравнения
-корни
характери стического уравнения
![]() (5)
(5)
Док-во:Пусть линия 2-го порядка пренадлежит II-му типу, тогда ее простейшее уравнение имеет вид (2).В этом случае:
I1=
![]()
I2=
![]()
Тогда
![]() и
и
![]() корни (5), тоесть
корни (5), тоесть
![]() .
.
![]()
![]()
Найдем I3:
I3=
Получаем (6).
Пусть линия (1) имеет простейшее уравнение (3)
I1=
I2=0
I3=

![]()
Получаем вид (7).
Пусть линия (1) имеет вид (4)
I1=
I2=0;
I3=0;
К2=![]()
![]()
Следовательно, имеем вид (8).
Доказано.
§23. Таблица для определения вида линии 2-го порядка по ортогональным инвариантам.
Пусть в ОДСК линия 2-го порядка задана общим уравнением вида (1)
Т-ма: В следующей таблице даны необходимые и достаточные условия каждого из девяти класов линий 2-го порядка:
Тип лин. |
Призн. типа |
Простейшее уравнение |
Признвида |
Канон ур. |
Название |
Центральные |
I2≠0 |
|
I2>0 I1* I3<0 |
|
элипс |
I2>0 I1 I3>0 |
|
Мним. элипс |
|||
I2>0 I3=0 |
|
пара мним. пр-ых |
|||
I2<0 I3≠0 |
|
гипербола |
|||
I2<0 I3=0 |
|
пара перес. пр-ых |
|||
нецентр |
I2=0 I3≠0 |
|
I2=0 I3≠0 |
|
парабола |
Прямая центров |
I2=0 I3=0 I1≠0 |
|
I2=0 I3=0 I1≠0 K2<0 |
|
пара парал. пр. |
I2=0 I3=0 I1≠0 K2=0 |
|
пара совп. пр. |
|||
I2=0 I3=0 I1≠0 K2>0 |
|
пара мн. парал. прям. |
Доказательство.
1) Пусть I2>0,
I1*
I3<0,тогда
корни характеристического уравнения
![]()
имеют
одинаковые знаки, I2=![]() . Поскольку I1*
I3<0,
то знак I1
будет одинаковым со знаком
, а I3
имеет знак противоположный им.
Следовательно, если в простейшем
уравнении линии последнее слагаемое
перенести в правую часть и разделить
на него, то получим уравнение
. Поскольку I1*
I3<0,
то знак I1
будет одинаковым со знаком
, а I3
имеет знак противоположный им.
Следовательно, если в простейшем
уравнении линии последнее слагаемое
перенести в правую часть и разделить
на него, то получим уравнение
,и посколько в
знаменателях величины положительные,
то имеем каноническое уравнение элипса
с полуосями
![]()
![]() ,
.
,
.
2) Пусть I2>0
I1*
I3>0,
тогда
и I3
имеют одинаковые знаки.Следовательно,
получим уравнение вида

- каноническое уравнение мнимого элипса.
3) Пусть I2>0
I3=0
Тогда простейшее уравнение будет иметь
вид
![]() , I2>0,
следовательно -
, I2>0,
следовательно -![]() .Получим
каноническое уравнение пары мнимых
прямых.
.Получим
каноническое уравнение пары мнимых
прямых.
4) Пусть I2<0,
I3≠0,
имеют разные знаки. Пусть![]() имеет знак одинаковый с I3,тогда
имеет знак одинаковый с I3,тогда

- гипербола с полу
осями
![]() , .
, .
5) Пусть I2<0,
I3=0
Тогда простейшее уравнение линии имеет
вид
,где
имеют разные знаки. если
![]() ,а
,а![]() ,то
,то
- пара пересекающихся прямых.
6) Пусть I2=0,
I3≠0,
![]() - простейшее уравнение линии,что и
является каноническим уравнением
параболы.
- простейшее уравнение линии,что и
является каноническим уравнением
параболы.
7) Пусть I2=0,
I3=0,
I1≠0,тогда
простейшее уравнение линии имеет вид:
![]() .Если K2<0 – имеем каноническое уравнение
пары паралельных прямых;Если K2=0 – имеем
каноническое уравнеие пары совпадающих
прямых;Если K2>0 – имеем каноническое
уравнение мнимых паралельных
прямых.Поскольку все признаки видов
взаимоисключающие друг друга, то
использую метод от противного можно
доказать все.Следствие:Для того, чтобы
линия 2-го порядка заданая относительно
ОДСК общим уравнением вида (1) распадалась
на 2 прямые необходимо и достаточно,
чтоб I3=0. Доказательство:
Из доказательства теоремы
следует, что для линий I-й группы при
I3=0 получим пару пересекающихся прямых
и для III-й группы – все линии распадаются
на 2 прямые.
.Если K2<0 – имеем каноническое уравнение
пары паралельных прямых;Если K2=0 – имеем
каноническое уравнеие пары совпадающих
прямых;Если K2>0 – имеем каноническое
уравнение мнимых паралельных
прямых.Поскольку все признаки видов
взаимоисключающие друг друга, то
использую метод от противного можно
доказать все.Следствие:Для того, чтобы
линия 2-го порядка заданая относительно
ОДСК общим уравнением вида (1) распадалась
на 2 прямые необходимо и достаточно,
чтоб I3=0. Доказательство:
Из доказательства теоремы
следует, что для линий I-й группы при
I3=0 получим пару пересекающихся прямых
и для III-й группы – все линии распадаются
на 2 прямые.