10.2 Приклади побудови рс інтегро-інтерполяційним методом

Побудуємо РС інтегро-інтерполяційним методом для рівняння теплопровідності

(10.1)

Із змінним коефіцієнтом ,

Для побудови РС розглянемо шаблон:

Рис 10.1

Позначимо середні точки інтервалів сітки напівцілими індексами і виконаємо інтегрування (1) по заштрихованій області:

(10.2)

(10.3)

Дане балансове співвідношення є точним для заштрихованої комірки. Перший інтеграл обчислюємо за формулою середніх прямокутників, а другий - за формулою правих прямокутників. Зауважимо, що рівняння (10.2) після інтегрування є рівнянням балансу тепла для виділеної комірки.

Введемо позначення q=-KU , яке виражає потік тепла. Тобто другий інтеграл в отриманому співвідношенні дає кількість тепла, яке залишається в стержні за рахунок теплових потоків на відрізку .

Перший інтеграл являє собою зміну потоку тепла в стержні на проміжку часу τ. Останній інтеграл – це різниця потоків тепла на вході і виході . Тоді використовуючи формули наближеного інтегрування, з передостаннього співвідношення маємо:

(10.4)

(10.5)

Підставляючи (10.4) і (10.5) в (10.3) отримаємо на рівномірній сітці:

(10.6)

З (10.6) слідує, що

(10.7)

Перетворимо (10.7) і маємо: 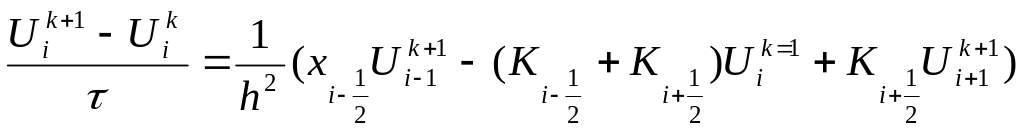(10.8)

Таким чином ми отримали ІІМ РС (10.8) для рівняння теплопровідності із змінним коефіцієнтом теплопровідності. Якщо К(х) =К=const, то отримана з (10.8) – неявна РС .

Отриману різницеву схему далі можна розв’язувати методом прогонки. Представимо (10.8) в прогоночному вигляді:

(10.9)

Коефіцієнти прогонки:

(10.10)

Розв’язок знаходиться методом прогонки:

(10.11)

Самостійно показати, що умови стійкості методу прогонки виконуються, і що дана схема володіє монотонністю.

Завдання: побудувати РС для рівняння теплопровідності із розривним коефіцієнтом, тобто з К1 та К3.

11. Різницеві схеми для рівнянь гіперболічного типу

Основні терміни і поняття:

Як відомо з курсу математичної фізики, типовим представником рівнянь гіперболічного типу є рівняння коливання деякої матеріальної субстанції (струн, стержнів, мембран, акустичні коливання).

Розглянемо побудову РС для першої крайової задачі для одновимірного рівняння коливання.

11.1 Постановка задачі

Як відомо, перша крайова задача для рівняння коливання струни записується наступним чином:

Як відомо з курсу математичної фізики, дана задача поставлена коректно (розв’язок її існує, він єдиний, стійкий, тобто розв’язок неперервно-залежний від початкових і граничних даних).

11.2 Рс задачі.

Для побудови РС даної задачі, покриємо область неперервної зміни аргументів різницевою сіткою з кроками h i τ, де

Для апроксимації задачі (11.1)-(11.5) скористаємося мінімальним 5-точковим шаблоном у вигляді хреста. Причому в даному шаблоні, навідміну від раніше розглянутих нами використовується три часові шари: (К-1), К, (К+1). Тому побудовані РС називаються трьохшаровими або трьохярусними.

Їх застосування вимагає, щоб при знаходженні значення на верхньому шарі необхідно значення даної функції на шарах і , які повинні зберігатись в пам’яті ЕОМ. Апроксимувавши другі похідні в рівнянні (11.1) їх скінченнорізницевими аналогами та підставивши їх в один отримали наступну систему алгебричних рівнянь :

(11.6)

Різницеві рівняння (11.6) мають порядок апроксимації 0(h²+τ²). Розвязок (11.6)на (К+1) шарі виражається явним числом і має вид

(11.7)

Для проведення числових розрахунків по формулі (11.7) повинні бути задані значення функції на двох попередніх шарах k-1 і k. Апроксимація граничних умов (11.2) і (11.3):

(11.8)

, (11.9)

(11.4) , (11.10)

(11.5) (11.11)

Остання формула означає, що друга початкова умова (11.3) апроксимована з порядком (0()). Недоліком отриманої РС є те, що вона має перший порядок точності по часу. Але ми можемо побудувати РС задачі (11.1)-(11.5), яка б мала порядок точності (0(h²+²)). Тому, при апроксимації (11.5). можна скористатись уточненою різницею . Однак, це призведе не до явної схеми, оскільки буде задіяно три шари : 0,1,2. Але ми поступимо по-іншому, а саме, розкладемо першу похідну в ряд Тейлора:

(11.12)

Різницевим аналогом (11.12) служить:

(11.13)

враховуючи рівняння (11.1), член замінимо на і перепишем (11.13) так:

(11.14)

З (11.14) маємо:

(11.15)

З (11.11) маємо:

(11.16)

Отримана різницева схема (11.7)-(11.10) і формула (11.16) побудовано з точністю 0(h²+τ²).

Можна показати що дана схема стійка при .Для того, щоб показати стійкість РС, розв’язок (11.6) шукаємо у вигляді:

(11.17)

- це частинні розв’язки

І-уявна одиниця

φ- довільне число

q-число, що необхідно знайти

h- крок сітки

(11.18)

(11.19)

(11.20)

Підставляючи (17.17) в (17.7) і скорочуючи на , отримаємо рівняння (17.18)

(11.18)

Будемо вважати, що різницеве рівняння (11.7) стійке, якщо обидва корені ( q1 і q2) рівняння (11.18) не перевищують 1. Нехай q1, q2- корені даного рівняння . Якщо обидва корені дійсні, то в силу того, що , по теоремі Вієта, тоді знайдеться таке φ, що одне з |q1|≥1, a |q2|≤1. Якщо ж корені комплексно спряжені, тобто , , то |q1|=|q2|=1

Таким чином, різницеве рівняння (11.7) стійке, якщо при всіх дійсних φ виконується умова(11.19)

Остання нерівність виконується для всіх φ, якщо τ≤h . Умова (11.19) є умовою стійкості побудованої РС . Більш строге обґрунтування стійкості РС можна дати, використовуючи принцип max для РС.