
- •2. Основна теорема теорії мн-нів.
- •3. Критерій розв’язуваності конгруенцій з одним невідомим першого степеня.
- •4. Основна теорема арифметики.
- •5. Знаходження оберненої матриці за допомогою визначників
- •6.Розв’язування с-ми лінійних рівнянь (слр) матричним способом. Формули Крамера.
- •7. Властивості множення матриць.
- •8. Критерій визначеності с-ми лінійних рівнянь (слр)
- •9. Критерій сумісності с-ми лінійних рівнянь .
- •1 0. Власт. Лз та лнз систем векторів.
- •11. Означення та вл-сті паралельних і розбіжних прямих на площині Лобачевського.
- •Дедекіндів переріз відрізка np
- •13. Аксіома Лобачевского. Основні факти геометрії.
- •14 Довжина дуги лінії на поверхні. Перша квадратична форма.
- •15. Дотична пряма і нормальна площина до гладкої просторової лінії. Виведення рівнянь.
- •16. Принцип двоїстості на проективній площині і в просторі. Теорема Дезарга.
- •1. Дано:
- •2. Дано:
- •17 Рухи. Властивості рухів. Класифікація рухів. Рухи
- •18.Рівняння площини і прямої в просторі.
- •1.Канонічне рівняння прямої.,
- •4. Параметричне р-ня прямої.
- •19.Змішаний добуток 3-х векторів. Геометр. Зміст змішаного добутку.
- •20.Векторний добуток 2-х векторів. Геометр. Зміст векторного добутку.
- •22. Похідна ф-ції комплексної змінної. Критерій існування. Умови Коші-Рімана.
- •23. Визначений інтеграл із змінною верхньою межею. Існування первісної неперервної ф-ції. Теорема Ньютона-Лейбніца.
- •24.Основні теореми диференціального числення (Ферма, Лагранжа, Коші, Роля)
- •26. Показникова і тригонометричні ф-ції в комплексній області.
- •27.Неперервні ф-ції та її властивості (теореми Больцано-Веєштраса I-II).
- •28. Означення границі ф-ції за Гейне і Коші.
- •30. Теорема Больцано – Вейєрштрасса (про підпослдовність).
4. Параметричне р-ня прямої.
Виберем яку-небудь
афінну с-му коорд. і задамо пряму d
напрямним![]() і
т.
.Т.
і
т.
.Т.![]()
коли
і
колінеарні, тобто коли
число t:
=t
.
Це співвідношення в коорд. запишеться
так:
коли
і
колінеарні, тобто коли
число t:
=t
.
Це співвідношення в коорд. запишеться
так:
![]() чи
(4*)
чи
(4*)
![]() -
параметричне
р-ня прямої з параметром t.
-
параметричне
р-ня прямої з параметром t.
Отже
дійсного t
точка з
координатами (x,y,z)
,яка задовільняє умовам (4*)
лежить на прямій d.Обернено
,якщо (x,y,z)
– точка прямої d
,то завжди знайдеться таке t,що
x,y,z
виражаються через
![]() за
допомогою рівності (4*).
за
допомогою рівності (4*).
19.Змішаний добуток 3-х векторів. Геометр. Зміст змішаного добутку.
Озн. Змішаним
добутком не компланарних векторів
![]() ,
взятих в даному порядку наз. Об’єм
паралелепіпеда, побудованого на цих
векторах, взятий із знаком „+”, якщо
базис
правий і із знаком „-”, якщо цей базис
лівий. Змішаний добуток компланарних
векторів рахується =0.
,
взятих в даному порядку наз. Об’єм
паралелепіпеда, побудованого на цих
векторах, взятий із знаком „+”, якщо
базис
правий і із знаком „-”, якщо цей базис
лівий. Змішаний добуток компланарних
векторів рахується =0.
Змішаний добуток
векторів
познач. Так:
![]() або
або![]() .
.
Виведемо формулу для обчислення змішаного добутку через коорд. векторів.
Лема. Які
б не були
-й
базис
![]() і ортонормований правий базис
і ортонормований правий базис
![]() ,
має місце рівність
,
має місце рівність
=(
)![]() .
.
Теорема.
Якщо вектори
в
довільному базисі
![]() мають коорд.
мають коорд.
![]() ,
,
![]() ,
,
![]() ,
то
,
то
=![]()
![]() (*)
(*)
Дов. Якщо вектори
компланарні, то рівність (*) правильна.
Нехай
деякий ортонормований правий базис, а
![]() -
визначник, який записаний в правій
частині рівності (*). Тоді за властивістю
базисів будемо мати:
-
визначник, який записаний в правій
частині рівності (*). Тоді за властивістю
базисів будемо мати:
![]() .
.
Поск.
![]() за властивістю базисів =1, то одержимо:
за властивістю базисів =1, то одержимо:![]() (**).
(**).
За лемою чисельник правої частини рівності (**) = , а знаменник = , тому з рівності (**) рівність (*).
Якщо базис
ортонормований, то
![]() ,
тому справедливе твердження:
,
тому справедливе твердження:
Наслідок. Якщо вектори в ортонормованому базисі мають коорд. , , , то
=![]() ,
де
,
де
![]() =1,
якщо базис
правий і
=-1,
якщо –лівий.
=1,
якщо базис
правий і
=-1,
якщо –лівий.
Вл-ті змішаного добутку:
Для
-х
векторів
і
![]() і
-го числа
і
-го числа
![]() мають місце наст. рівності:
мають місце наст. рівності:
1.
=![]()
2.
=![]() ,
=
,
=![]()
3.
![]() ,
,
![]() ,
,
![]()
4.
![]() .
.
Дов. Виберемо
ортонормований правий базис
і задамо дані вектори в координатах
![]() ,
,
,
,
,
,
![]() .
.
1)
=![]() .
.
Геометр. зміст.
Об’єм паралелепіпеда побудованого на векторах = модулю змішаного добутку цих векторів.
20.Векторний добуток 2-х векторів. Геометр. Зміст векторного добутку.
Озн. Векторним
добутком не колінеарних векторів
і
![]() наз. Такий вектор
наз. Такий вектор
![]() ,
що
,
що
1)
![]()
2)
![]()
![]() і
і
3) вектор напрямлений так, що ( ) права трійка.
Векторний добуток колінеарних векторів =0.
Векторний добуток
векторів
і
познач.
![]() або
або
![]() .
.
Теорема1. Які б не були вектори , і = .
Теорема. Для
того, щоб вектори
і
були колінеарні
,
щоб
![]() .
.
Дов. Необхід.
і
колінеарні
![]() .
.
![]()
![]() .
.
Дост.
.
![]()
![]() - вектори спів напрямлені.
- вектори спів напрямлені.
Теорема. Якщо вектори і в ортонормованому базисі мають коорд. , , то вектор має коорд.:
![]() (**).
(**).
Дов. Нехай x, y, z- коорд. вектора . Тоді
=![]() ,
тому
,
тому
![]() =
=![]() .
За теор.1
=
.
За теор.1
=![]() x=
.
Аналог.
одерж.: y=
x=
.
Аналог.
одерж.: y=![]() ,
z=
,
z=![]() .
Тоді згідно формули для обчислення зм.
добутку будемо мати:
.
Тоді згідно формули для обчислення зм.
добутку будемо мати:
![]() ,
,
![]() ,
,
![]() .
.
Тобто
=![]() =
=![]() (*).
(*).
Вл-ті вект. добутку:
Для
-х
векторів
,
і
і для
-го
![]() справедливі рівності:
справедливі рівності:
1.
=![]()
2.
![]() ,
,
![]()
3. .
![]() ,
,
![]() .
.
Дов. Виберемо ортонормований правий базис і задамо дані вектори в координатах , , . Використовуючи формулу (*) довод. вл-ті.
Вл-ть 3. .
Задамо дані вектори
в координатах
![]() (x,y,z),
(x,y,z),
![]() ,
,
![]() .
.
За формулою (**)
одерж., що
![]() .
.
Аналог. одерж.
![]() ,
,
![]() .
Отже, дана вл. справедлива.
.
Отже, дана вл. справедлива.
Лема
Для
-х
векторів
і
справедл. рівність
=![]() .
.
Геометр. зміст.
Площа паралелограма побудованого на векторах і чисельно = модулю векторного добутку .
![]()
![]() .
.
*** 21.Застосування похідної до дослідження ф-ції на монотонність і знаходження екстремуму. Монотонність і похідна
Т.1. (Достатня умова строгої монотонності ф-ції на проміжку)
Нехай
![]() ,
диференційована на
,
диференційована на
![]() .
Якщо
.
Якщо
![]() ↗
на
.
↗
на
.
Д оведення.
Візьмемо
оведення.
Візьмемо
![]()
a x1 c x2 b
Застосуємо до![]() і
ф-ції
т.
Лагранжа (умови її виконуються), будемо
мати:
і
ф-ції
т.
Лагранжа (умови її виконуються), будемо
мати:
![]()
P.S. Аналогічна теорема з очевидними змінами буде справедлива і для монотонного спадання:
Т.2................................................. (доведення аналогічне)
Очевидно, що теореми обернені до тільки що розглянутих будуть невірними.
П-д:
![]() ,
яка ↗
на
,
яка ↗
на
![]() ,
але умова
,
але умова
![]() не виконується в т.x=0.
Там
не виконується в т.x=0.
Там
![]() .
.
Критерії нестрогої монотонності ф-ції на інтервалі:
Т.3.
Нехай
,
диференційована на
.
Для того щоб
була ⇟
на
⇔,
щоб
![]()
■ Доведення: Необхідність
(Достатність доводиться так само, як і в Т.1)
Візьмемо
![]() тоді матимемо, що:
тоді матимемо, що:
![]()
■ Аналогічною є теорема для монотонного не спадання:
Т.4.........................
Критерії строгої монотонності.
Т.5. Для того, щоб була ↗ на ⇔, щоб:
1)
![]()
2) Ніякі точки з
![]() ,
в яких
не утворювали б відрізка.
,
в яких
не утворювали б відрізка.
■ Доведення: Необхідність
Нехай
![]() ↗
на
,
значить
↗
на
,
значить
![]() ⇟,
а тому за Т.3
⇟,
а тому за Т.3
Покажемо, що 2) виконується.
Прип., що вона не
виконується. Тобто
![]()
![]() ,а
звідси за наслідком із т. Лагранжа ⇒
,а
звідси за наслідком із т. Лагранжа ⇒![]() ,
,
тому
,
,
тому
![]() ,
що неможливо, бо
,
що неможливо, бо
![]() і
↗
.Суперечність.
і
↗
.Суперечність.
Достатність
Нехай виконуються умови 1), 2).
З 1) ⇒,
що
⇟
на
.
Прип., що
не буде ↗,
тобто
![]() ,
звідси, і з того, що
⇟
маємо, що
на
,
звідси, і з того, що
⇟
маємо, що
на
![]() ,
тобто
на
а це протирічить умові теореми.
Суперечність. ■
,
тобто
на
а це протирічить умові теореми.
Суперечність. ■
Аналогічною є теорема про строге спадання ф-ції:
Т.6................................
P.S. В умовах 2-х останніх теорем вимагається диференційовність ф-ції на . Ці теореми повністю вирішують проблему монотонності диф. на проміжку ф-ції. З допомогою похідної виріш. проблема екстремальних точок.
Похідна і екстремум ф-ції
Озн:
Нехай
визначена
в
![]() .
Т.
наз. точкою максимуму(мінімуму), якщо
.
Т.
наз. точкою максимуму(мінімуму), якщо
![]() :
:![]() ,
крім т.
⇒
,
крім т.
⇒
![]() (
(![]() ).
).
Точки max і min ф-ції наз. точками екстремуму ф-ції, а значення ф-ції в цих точках – екстремальними.
Т.1. (Необхідна умова екстремуму ф-ції)
Якщо т.
є т. екстремуму ф-ції і якщо в цій т.
похідна,
то
![]() (
в точках екстремуму
або не існує ).
(
в точках екстремуму
або не існує ).
П-д
![]()
![]() ,
але екстремуму немає.
,
але екстремуму немає.
Оск. екстремум може бути в точках, де або не існує, то по-перше, назвемо ці точки критичними. По-друге, перед нами стоїть завдання, як серед цих точок ’’виловити’’ точки екстремуму.
Т.2. (перші достатні умови існування екстремуму)
Нехай
![]() задана в
(
– критична) і
задана в
(
– критична) і
![]() диференційована в лівому і правому пів
околах.
диференційована в лівому і правому пів
околах.
Тоді, якщо при проходженні через точку зліва на право похідна змінює знак:
+ → – то в точці має max
– → + то min
не змінює знаку – екстремуму немає
□ Доведемо 1. Це
означає, що
![]() (
(![]() -
розмір околу)
-
розмір околу)
P.S.
Всюди в подальшому ми будемо досліджувати
той випадок коли точка
є точкою неперервності функція
.
Для доведення нашої теореми в першому
випадку. Треба довести, що
![]() (*). Візьмемо
(*). Візьмемо
![]() тоді
тоді
![]() може попасти на
може попасти на
![]() ,
або
,
або
![]() .
Нехай
попав на
.
Розгл.
.
Нехай
попав на
.
Розгл.
![]() ,
ясно, що тут
неперервна
і на
,
ясно, що тут
неперервна
і на
![]() диференційована. Тому за теоремою
Лагранжа матимемо:
диференційована. Тому за теоремою
Лагранжа матимемо:
![]()
звідси маємо: ⇒↗.
Аналогічно розглядаються і інші випадки. ■
Т.3. (другі достатні умови існування екстремуму)
Нехай
двічі диференційована в критичній точці
.
Тоді, якщо
![]() ,
якщо
,
якщо
![]() ,
якщо
,
якщо
![]() потрібні ще дослідження
потрібні ще дослідження
Зауважимо, що якщо в
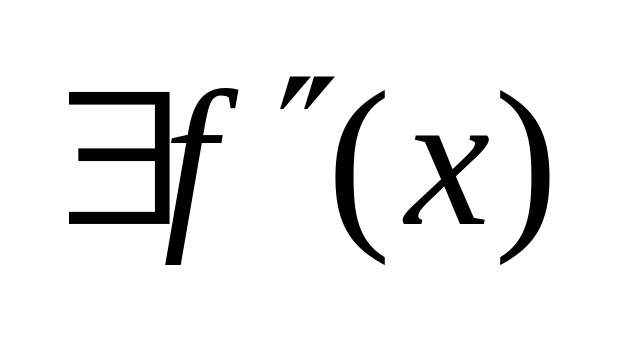 ,
то в О(
),
як випливає з озн.
,
то в О(
),
як випливає з озн.
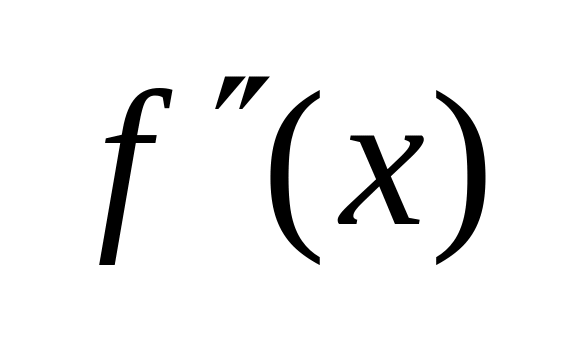 повинно
повинно
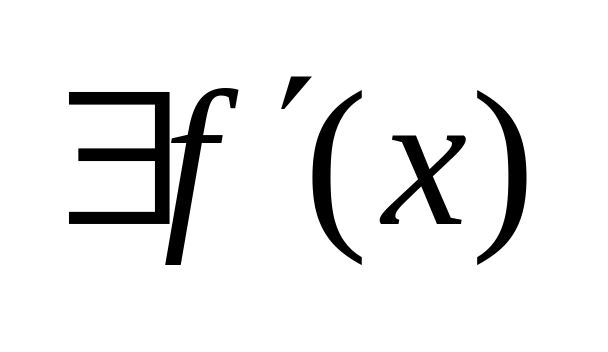 .
.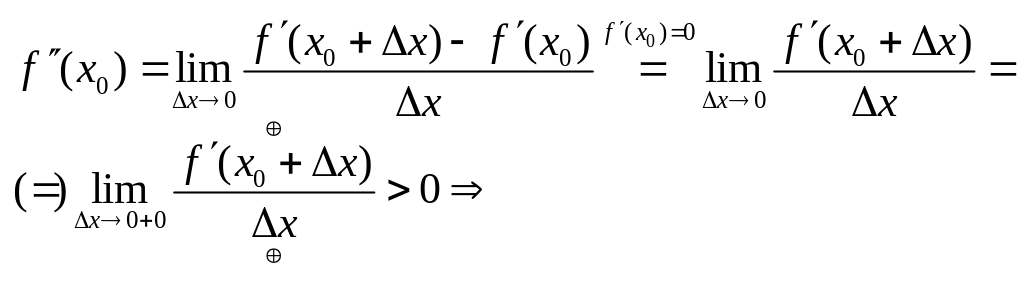
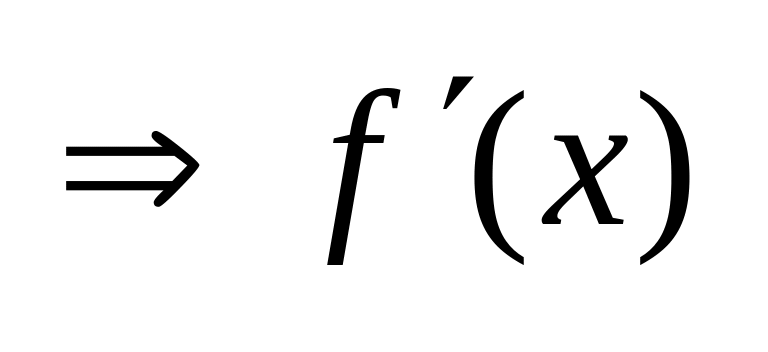 на інтервалі
на інтервалі
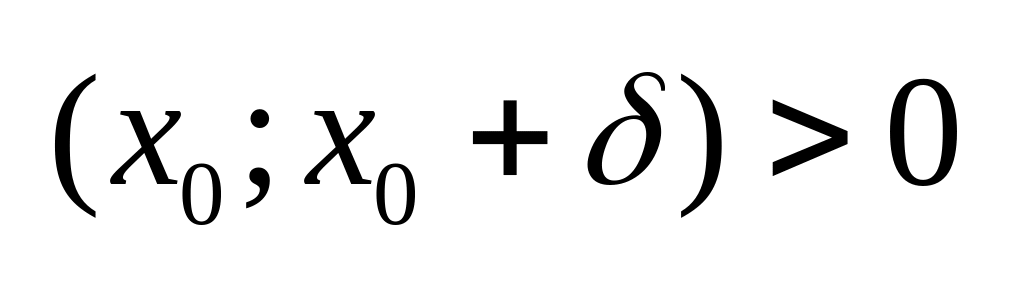 .
.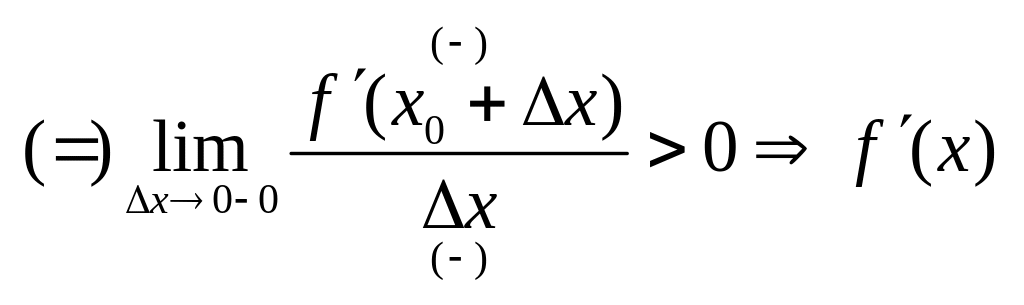 на інтервалі
на інтервалі
 .
.Нехай
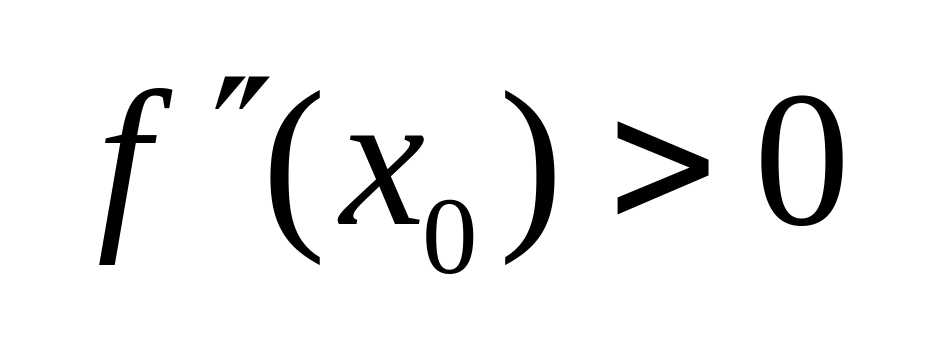 .
Тоді .....
.
Тоді .....Тоді при проходженні через т.
 змінює знак з „-” на „+”. А за доведеною
раніше теоремою означає, що в т.
має мінімум. Випадок
змінює знак з „-” на „+”. А за доведеною
раніше теоремою означає, що в т.
має мінімум. Випадок
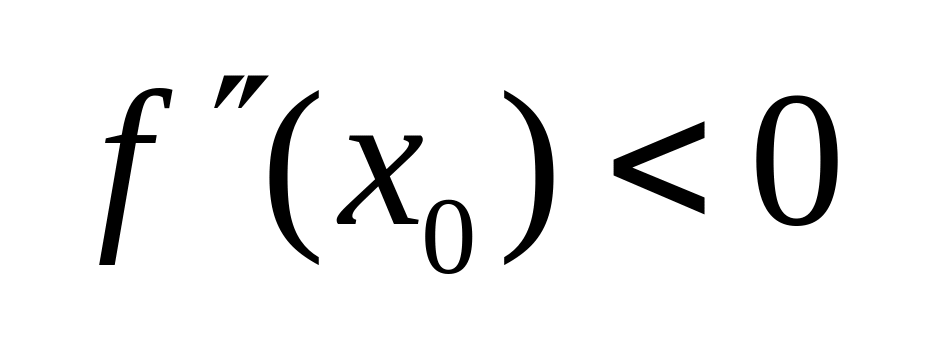 розглядається аналогічно. (випадок
коли
розглядається аналогічно. (випадок
коли
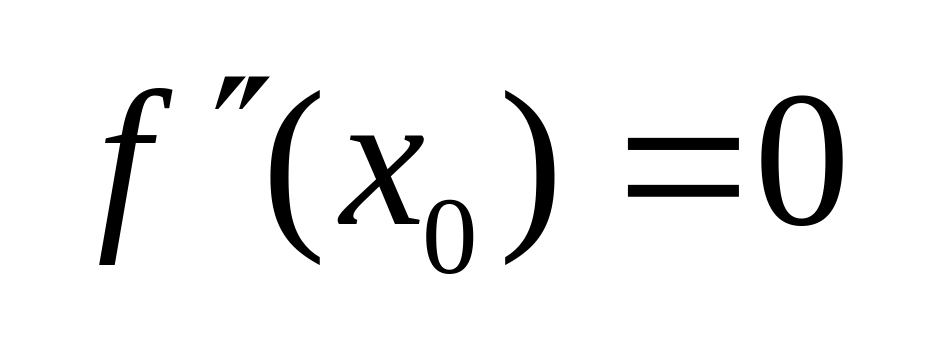 в Ільїн Садовн.-Сендов).
в Ільїн Садовн.-Сендов).Схема дослідження ф-ції на екстремум:
знаходимо похідну ф-ції і критичні точки цієї ф-ції;
наносимо на числову вісь одержані критичні точки, а також точки розриву ф-ції. Ці точки розбивають область визначення ф-ції на інтервали.
знаходимо знак похідної на кожному з цих інтервалів.
з допомогою картинки визначаємо точки екстремуму (математичні проміжки монотонності ф-ції)
 ,
,
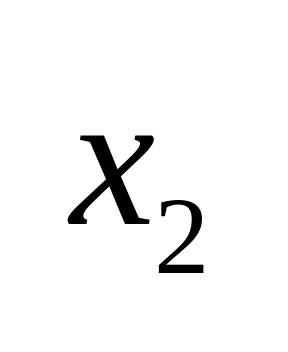 –
екстремуму немає.
–
екстремуму немає.
В цьому параграфі ми навчилися, як за допомогою похідної знаходити проміжки монотонності ф-ції, а також точки екстремуму. Виявляється що похідна допомагає встановити форму графічної ф-ції на тому чи іншому проміжку. Тобто чи на якомусь проміжку графік ф-ції має форму вгнутості чи форму опуклості, ці проблеми розв’яжемо в наступному параграфі.
