
- •2. Основна теорема теорії мн-нів.
- •3. Критерій розв’язуваності конгруенцій з одним невідомим першого степеня.
- •4. Основна теорема арифметики.
- •5. Знаходження оберненої матриці за допомогою визначників
- •6.Розв’язування с-ми лінійних рівнянь (слр) матричним способом. Формули Крамера.
- •7. Властивості множення матриць.
- •8. Критерій визначеності с-ми лінійних рівнянь (слр)
- •9. Критерій сумісності с-ми лінійних рівнянь .
- •1 0. Власт. Лз та лнз систем векторів.
- •11. Означення та вл-сті паралельних і розбіжних прямих на площині Лобачевського.
- •Дедекіндів переріз відрізка np
- •13. Аксіома Лобачевского. Основні факти геометрії.
- •14 Довжина дуги лінії на поверхні. Перша квадратична форма.
- •15. Дотична пряма і нормальна площина до гладкої просторової лінії. Виведення рівнянь.
- •16. Принцип двоїстості на проективній площині і в просторі. Теорема Дезарга.
- •1. Дано:
- •2. Дано:
- •17 Рухи. Властивості рухів. Класифікація рухів. Рухи
- •18.Рівняння площини і прямої в просторі.
- •1.Канонічне рівняння прямої.,
- •4. Параметричне р-ня прямої.
- •19.Змішаний добуток 3-х векторів. Геометр. Зміст змішаного добутку.
- •20.Векторний добуток 2-х векторів. Геометр. Зміст векторного добутку.
- •22. Похідна ф-ції комплексної змінної. Критерій існування. Умови Коші-Рімана.
- •23. Визначений інтеграл із змінною верхньою межею. Існування первісної неперервної ф-ції. Теорема Ньютона-Лейбніца.
- •24.Основні теореми диференціального числення (Ферма, Лагранжа, Коші, Роля)
- •26. Показникова і тригонометричні ф-ції в комплексній області.
- •27.Неперервні ф-ції та її властивості (теореми Больцано-Веєштраса I-II).
- •28. Означення границі ф-ції за Гейне і Коші.
- •30. Теорема Больцано – Вейєрштрасса (про підпослдовність).
22. Похідна ф-ції комплексної змінної. Критерій існування. Умови Коші-Рімана.
Аналіз означення похідної з R аналізу показує, що воно може бути перенесене на ф-ції з комплексним аргументом.
Озн.
Нехай w=f(z)
– ф-ція задана в деякому
![]() .
Якщо
.
Якщо
![]() ,
то її наз. похідною ф-ції в т.
,
то її наз. похідною ф-ції в т.![]() .
.
Озн. буде коректне,
якщо ця ф-ція, задана на множині
![]() і
т.z0
буде граничною для мн.E.
Похідна матиме вигляд:
і
т.z0
буде граничною для мн.E.
Похідна матиме вигляд:
![]() .
.
Пр-д.
Нех. є ф-ція
![]() ,
x
задана на множині R
(E=R).
,
x
задана на множині R
(E=R).
![]() .
Поширимо цю ф-цію на всю
мн. і задамо
.
Поширимо цю ф-цію на всю
мн. і задамо
![]()
Візьмемо т. з і з’ясуємо чи має ця ф-ція похідну в ній.
![]() ,
,
Границі немає в жодній т.z0, а це означає що ф-ція w(z) – не диф. в жодній т. мн. похідної залежить від мн. на якій задана ф-ція.
Вимагаючи від ф-ції
аргументу
похідної
в деякій т.z0,
на всій мн.
,
ми ставимо на ф-цію більш жорстку вимогу
ніж при аналогічній постановці для
ф-ції на R
прямій. Тоді ми вимагаємо
відповідної
границі вздовж
напрямку
прямування
![]() ,
і щоб вони були рівні. (На відміну від
дійсної прямої де цей напрямок один(сама
пряма)).
,
і щоб вони були рівні. (На відміну від
дійсної прямої де цей напрямок один(сама
пряма)).
Т. (Критерій диференційовності)
Нех. G
відкрита обмежена мн.
чисел.
Т. z0![]() .
.
Для того щоб ф-ція
![]() задана
в області G
була диф.в т. z0
необхідно і достатньо, щоб:
задана
в області G
була диф.в т. z0
необхідно і достатньо, щоб:
1) ф-ції та , як ф-ції 2-х R змінних були диф. в т. (x0y0),
(z0=x0+iy0)
2)в цій точці виконувалися рівності:
![]() умови Коші-Рімана.
умови Коші-Рімана.
Доведення. Необх. Нехай W=f(z) – диф. в т. z0=x0+iy0.
![]() За озн. похідної
маємо:
За озн. похідної
маємо:
![]() ,
,
![]() (2)
(2)
Оск.
![]() ,
,
![]()
Підставивши це в рівність (2) і виділивши дійсні і уявні частини одержимо:
![]()
Останні дві рівності,
враховуючи як ведуть себе
![]() ,
а також числа
,
а також числа
![]() не залежать від
не залежать від
![]() озн. що ф-ції
озн. що ф-ції
![]() і
і
![]() як ф-ції 2-х R
змінних диф. в точці (x0y0).
як ф-ції 2-х R
змінних диф. в точці (x0y0).
Позн.
![]()
![]() ,
,![]()
![]() .
.
З останніх 4-х рівностей маємо умови Коші-Рімана (1). Необх. доведена, причому
![]()
Дост.
Нех. 1) і 2) викон. Покажемо що ![]() :
:
З 1) матимемо, що:
![]() ,
(3),
,
(3),
де
![]() коли
коли
![]()
![]() (4).
(4).
![]()
Покладемо:
![]()
Підставивши в (3) і
(4) замість відповідних частин похідних
![]() і
і
![]() ,
помноживши (4) на
,
помноживши (4) на
![]() та
додавши її до (3) одержимо:
та
додавши її до (3) одержимо:
![]()
Звідси:
![]()
Останні два доданки
прямують до 0, бо![]() (1*)
(1*)
![]() при
при![]() Отже,
Отже,
![]()
23. Визначений інтеграл із змінною верхньою межею. Існування первісної неперервної ф-ції. Теорема Ньютона-Лейбніца.
Після того, як введено поняття інтеграла Рімана і вивчено його вл-сті, постає проблема, як його обчислювати. На практиці складно викор. озн. Розгл. Рімана із змінною верхньою межею.
Нех.
![]() .
Тоді за аддитивністю
.
Тоді за аддитивністю
![]() Тоді можна говорити про ф-цію
Тоді можна говорити про ф-цію
![]() .
Ця ф-ція наз.
із змінною верхньою межею. Вивчимо
власт. ф-ції F(x):
.
Ця ф-ція наз.
із змінною верхньою межею. Вивчимо
власт. ф-ції F(x):
Т. 1.
F(x)
![]() .
.
Дов.
Візьмемо
![]() і надамо йому приріст ∆х,
і одержимо ∆х+х.
Розгл.
і надамо йому приріст ∆х,
і одержимо ∆х+х.
Розгл.
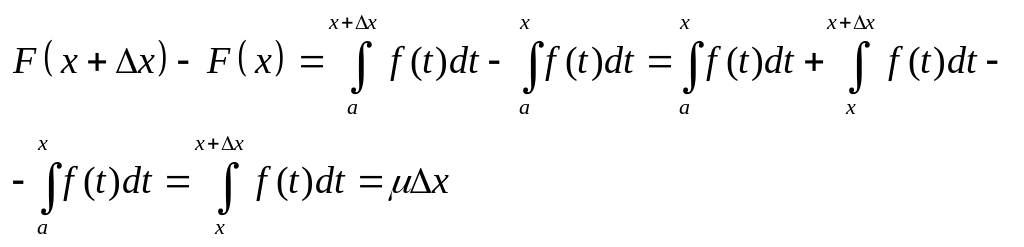 звідси маємо, що:
звідси маємо, що:
![]() .
.
Перейшовши в одержаній рівності до границі при ∆х → 0 і отримаємо за різницевим означенням неперервності F(x) .
Т. 2.
Якщо в умовах попередньої теореми
f(t)![]() т.
т.![]() ,
то ф-ція F(x)
диф. в т. х0
і F′(x0)
= f(x0).
,
то ф-ція F(x)
диф. в т. х0
і F′(x0)
= f(x0).
Дов. Розгл. величину:
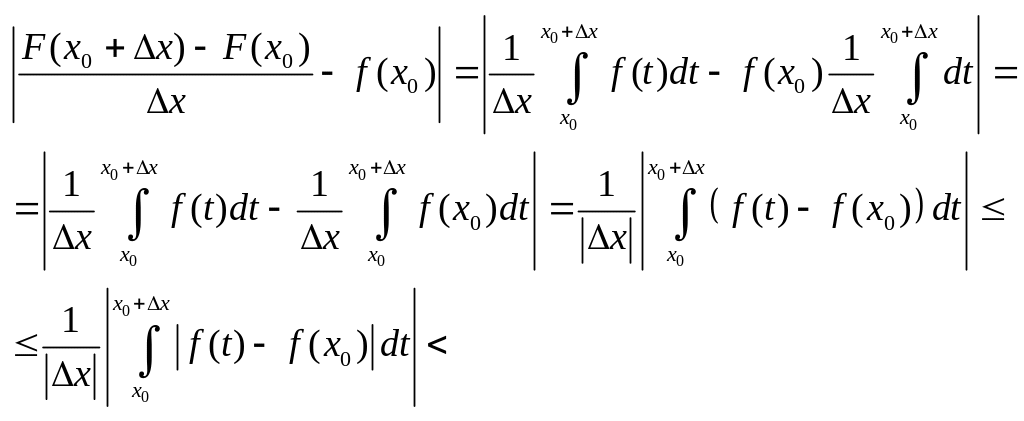 (1)
(1)
Те що f(t) означає:
![]() (2)
(2)
Візьмемо |∆х|<δ. Тоді в інтегралі (1) |t-х0|<δ. Тоді з (2) можна так продовжити (1):
![]()
Таким чином ми
довели, що
![]() .
.
Т. 3. (наслідок Т.2.,про первісної).
Якщо f(х) , то вона на цьому відрізку має первісну.
Т. 4. (формула Ньютона-Лейбніца).
Нехай f(х)
![]() і F(x)
– якась її первісна. Тоді справедлива
рівність:
і F(x)
– якась її первісна. Тоді справедлива
рівність:![]()
Дов.
Візьмемо
T-розбиття
![]() :
a=x0<x1<…<xk=b.
:
a=x0<x1<…<xk=b.
Розгл.:
![]()
![]()
Перейшовши в цій
рівності до границі при (Т)
0 і врахувавши,
що
![]() одержимо, що
одержимо, що
![]() .
Частковий випадок доведеної теореми:
.
Частковий випадок доведеної теореми:
Т.5.
Якщо
![]() ,
то справедливо:
,
то справедливо:
![]() ,
де F(x)
– одна з первісних на
.
,
де F(x)
– одна з первісних на
.
Дов.
З
![]()
