1.Теорема про єдиність та можливість представлення правильного дробу у вигляді суми елементарних.

Озн. Рац. дріб наз. правильним, коли степінь чисельника менший за степінь знам.

Т. " правильинй дріб можна представити у вигляді суми елементарних дробів.

Д ов. т-му спочатку для вип. правильного дробу: , де g(x) i h(x ) – взаємно прості deg f< deg (gh)

О-ки мн-ни g(x) i h(x ) взаємно прості, то $ мн-ни і : g(x) + h(x) = 1. Домножимо на f(x):

g(x)(f(x) )+h(x)(f(x) )=f(x) (3) , поділимо f(x) на h(x): hs+u=f

Тоді (3) можна записати: gu+hv=f (4), де deg u < deg h

v(x) – мн-член , який легко знайти, але в явному вигл. він нас не цікавить

deg(gu) < deg(gh), deg(f) < deg(gh)

Отже, deg (hv)<deg (gh), deg (v)<deg (gh), deg (v)<deg g, тобто цей правильний дріб ,

де g i h взаємнопрості.

Якщо мн-н g(x) розкладається на взаємонпрості множники , то міркуючи аналогічно можна відпов. дріб розкласти на суму правильних дробів в знамен. кожного з яких стоїть степінь деякого незвідного мн-на поля Р, який буде взаємнопростий із знамениками інш. дробів.

Розгл. . М-н g(x)=(p₁(x))^k1(p₂(x))^k2…(p_s(x))^ks,

p_i –незвідні в полі Р мн-ни, вони попарно прості.

Отже, дріб можна представити у вигляді:

, де .

Беремо з таких доданків : <deg (p^k) , буде:

=(p(x))^k-1s₁(x)+ , deg < deg (p)^k-1

=(p(x))^k-2s₂(x)+

………………………….. (5)

=(p(x))²s_k-2(x)+

=(p(x))s_k-1(x)+

З 1–го р–ня (5) маємо: deg <deg (p)^k deg <deg (p)^k-1

Отже, deg s₁<deg (p)

Міркуючи аналогічно отримаємо, що deg s_i < deg p, i=2…k-1

Звідси: deg <deg p.

Врахувавши (5) отрим.:

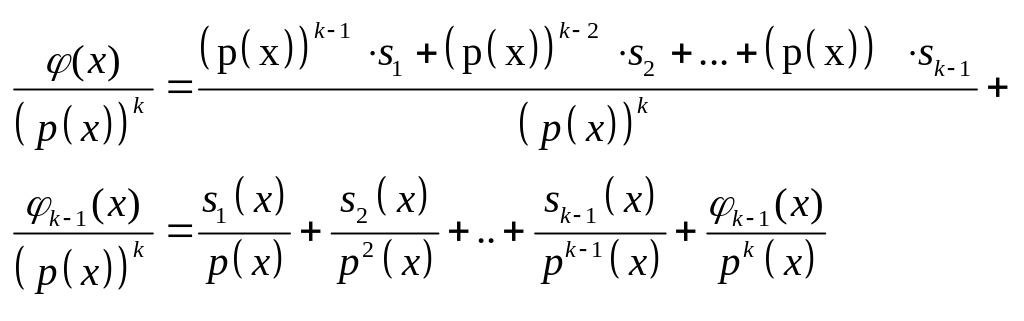
Отже, дріб представлений у вигл. суми елементарних дробів.

Т. " правильний дріб можна єдиним чином представити у вигляді суми елементарних дробів.

Дов. Прип., що деякий правильний дріб по крайній мірі двома способами представляється у вигляді суми елем. дробів. Віднявши від 1-го представлення 2-е і звівши подібні доданки отримаємо алгебраїчну суму елем. дробів, яка 0.

Прип., що знаменники цих дробів є степенями незвідних в полі Р мн-нів р₁(х), р₂(х), ...., р_l(х).

Нехай найбільший із степенів мн-на р_і(х), з яким він входить в цю суму буде к_і , і= 1…l.

Домножимо обидві чатини останньої рівності на вираз , , ...., (6)

Прип. елем. дріб знаменником якого є має вигляд: (7), де степінь строго менший степеня р₁, тобто, якщо ми обидві частини нашої р-ті домножимо на (6), то в 1-ій частині стоятиме 0 , а в другій стоятиме сума мн-нів і дробу

, який отримається із (7). Але всі р_і попарно взаємнопрості, отже, р₁(х) з ніяким із мн-нів чисельника скоротитися не може, тобто, отримаємо, що рац. дріб = сумі мн-нів. Такого бути не може!

2. Основна теорема теорії мн-нів.

Т. 1. " мн-н (deg(f) 1) з R коефіцієнтами має хоча б 1 комплексний корінь.

Викор. цю т. доведемо осн. т. теорії мн-нів.

Т. (основна теорема теорії мн-нів)

" мн-н з коеф. def ≥1 має хоча б 1 корінь.

Дов. Нех. – мн-н з коеф., розгл. Мн-н – коеф. якого спряжені до коеф. f(z) спряжене до і розгл. добуток: , де , k=0…n

Розгл. .

Отже, мн-н буде мн-ном з R коеф. За т.1 $ хоча б 1 корінь мн-на то звідси Þ, що , або тобто розгл. число спряжене до лівої частини:

Отже, якщо α не є коренем f(z), то є коренем цього мн-на.

З даної т. $ ряд наслідків.

Н. 1: " мн-н з коеф. степеня >1 є звідним в полі чисел.

Н. 2: " мн-н однозначно, з точністю до порядку слідування множників можна представити у вигляді:

.

З н.1 Þ: Мн-н з коеф. є незвідним в полі чисел , коли його степінь буде = 1.

З н. 2 Þ: к-сть коренів мн-на з коеф., з врахуванням їх кратності, = степеню мн-на, тобто поле чисел є алгебраїчно замкнутим.

Н.3: " мн-н f(x), з R коеф., степеня >2 є звідним у полі R.

3. Критерій розв’язуваності конгруенцій з одним невідомим першого степеня.

Заг. вигляд конгруенції 1-го степеня з одним невідомим: . Дослідимо всі можливі випадки розв’язування лінійних конгруенцій.

І. Розгл. спочатку найбільш важливий випадок, коли а і т взаємнопрості, тобто (a,m)=1.

Якщо в підставити замість х всі лишки з повної с-ми, то за 1-ою т. про лишки лінійної форми, ах також перебігає всі значення з повної с-ми лишків, тому для одного і тільки одного значення х₁ число ах₁ потрапляє в той клас, до якого належить b , для нього отримаємо .

Отже у випадку (а,m)=1 лінійна конгруенція має лише один розв’язок: або x=x₁ + mt, .

Пр-д. .

Підставляючи лишки повної с-ми за модулем 8: ; знаходимо .

І І. Розгл. випадок, коли (a ,m)=d, d >1 і

В цьому випадку лінійна конгруенція розв’язку мати не може, оск. це суперечить тій вл-сті конгруенцій (частини конгруенції мають з модулем один і той самий НСД).

Дов.

,

Отже, – суперечність.

П-д. 6х ≡ 7 (mod 15)

(6, 15) = 3, але

Отже, конгруенція розв’язку немає.

I I I. Розгл. останній випадок, коли (а, m) = d, d > 1 і .

Тоді а = а₁d, b = b₁d , m = m₁d.

За відомою вл-стю конгруенцій обидві частини конгруенції і модуль можна поділити на d, після чого отримуємо

а₁х b₁ (mod m₁), (а₁ ,т₁)=1, що Û випадку І.

Отримана конгруенція має розв’язок .

Щоб знайти класи розв’язків за модулем т відзначимо, що всі лишки …, x₁ –m₁ , x₁ ,x₁ +m₁ ,…, x₁ +(d-1)m₁ , x₁ +dm₁ ,… (*)

конгруентні з x₁ за модулем m₁ , належать за модулем m=m₁d різним класам, представниками яких є лишки:

. (**)

(

, k-r = cd , k=cd+r , )

Дійсно, різниця двох " таких чисел не ділиться на m, отже вони належать різним класам лишків за модулем m. Крім того для кожного лишку з ряду (*) завжди знайдеться число з (**) таке, що їх різниця буде кратна m , отже такі числа належать одному класу лишків за модулем m. Тому в цьому випадку конгруенція буде мати d розв’язків: . П-д

Ділимо на НСД(15, 35, 55) =5, отримуємо

Методом підбору знаходимо: .

Тоді для даної конгруенції маємо п’ять розв’язків: .

Критерій розв’язку лінійної конгруенції :

І. якщо (a ,m)=1, то $! розв’язок;

І І. (a ,m)= d , d>1 і – розв’язку немає;

І І І. (a ,m)= d , d>1 і – $ d розв’язків.