
- •2. Основна теорема теорії мн-нів.
- •3. Критерій розв’язуваності конгруенцій з одним невідомим першого степеня.
- •4. Основна теорема арифметики.
- •5. Знаходження оберненої матриці за допомогою визначників
- •6.Розв’язування с-ми лінійних рівнянь (слр) матричним способом. Формули Крамера.
- •7. Властивості множення матриць.
- •8. Критерій визначеності с-ми лінійних рівнянь (слр)
- •9. Критерій сумісності с-ми лінійних рівнянь .
- •1 0. Власт. Лз та лнз систем векторів.
- •11. Означення та вл-сті паралельних і розбіжних прямих на площині Лобачевського.
- •Дедекіндів переріз відрізка np
- •13. Аксіома Лобачевского. Основні факти геометрії.
- •14 Довжина дуги лінії на поверхні. Перша квадратична форма.
- •15. Дотична пряма і нормальна площина до гладкої просторової лінії. Виведення рівнянь.
- •16. Принцип двоїстості на проективній площині і в просторі. Теорема Дезарга.
- •1. Дано:
- •2. Дано:
- •17 Рухи. Властивості рухів. Класифікація рухів. Рухи
- •18.Рівняння площини і прямої в просторі.
- •1.Канонічне рівняння прямої.,
- •4. Параметричне р-ня прямої.
- •19.Змішаний добуток 3-х векторів. Геометр. Зміст змішаного добутку.
- •20.Векторний добуток 2-х векторів. Геометр. Зміст векторного добутку.
- •22. Похідна ф-ції комплексної змінної. Критерій існування. Умови Коші-Рімана.
- •23. Визначений інтеграл із змінною верхньою межею. Існування первісної неперервної ф-ції. Теорема Ньютона-Лейбніца.
- •24.Основні теореми диференціального числення (Ферма, Лагранжа, Коші, Роля)
- •26. Показникова і тригонометричні ф-ції в комплексній області.
- •27.Неперервні ф-ції та її властивості (теореми Больцано-Веєштраса I-II).
- •28. Означення границі ф-ції за Гейне і Коші.
- •30. Теорема Больцано – Вейєрштрасса (про підпослдовність).
4. Основна теорема арифметики.
Т. " N число >1 або є простим, або може бути представлене, і, при тому єдиним способом у вигляді добутку простих чисел.
(Два представлення, які відрізняються лише порядком розмі-щення множників, вважаються однаковими).
Дов. І. Існування розкладу.
Нех. n = 2. Оск. 2 – просте число, то для n = 2 твердження т. є справедливим. Прип., що твердження справедливе " N чисел, які 2, але < деякого п , і дов. справедливість твердження для п.
Розгл.
![]() . Якщо п
– просте, то
твердження має місце. Якщо п
– складене,
то його можна записати у вигляді
п = п1п2
, де
. Якщо п
– просте, то
твердження має місце. Якщо п
– складене,
то його можна записати у вигляді
п = п1п2
, де
1 <n1
< n
і 1< n2
< n.
Для чисел
п1
і
п2
згідно з
індуктивним припущенням буде справедливим
![]() і
і
![]() .
Тоді
.
Тоді
![]() ,
тобто $-ня
розкладу "
п
доведено.
,
тобто $-ня
розкладу "
п
доведено.
ІІ.Єдиність розкладу.
Нехай п=2, це просте число, отже його розклад єдиний.
Прип., що розклад на прості множники єдиний для всіх N чисел, >2, але < п, і доведемо єдиність розкладу для п.
Якщо п – просте число, то його розклад є єдино можливим. Нехай п – складене, прип., що його можна розкласти на прості множники 2-а різними способами:
![]() і
і
![]() .
.
Тоді
![]() =
=![]() .
.
Ліва частина цієї
рівності ділиться на р1,
тоді на р1
повинен
ділитися один із множників добутку
![]() .
Нех.
.
Нех.
![]() .оск.
q1
– просте число і р1>1,
то
.оск.
q1
– просте число і р1>1,
то
![]() .
Поділимо обидві частини рівності на
,
і отримаємо
.
Поділимо обидві частини рівності на
,
і отримаємо
![]() =
=
![]()
Оск. і – числа ,< п, то згідно індуктивного припущення з останньої рівності випливає, що l = s, p2 = q2, …, pl = qs .
Отже, теорему доведено.
Згідно з осн. т.
арифметики "складене
число n>1
можна
представити у вигляді добутку простих
чисел. Серед цих простих мн-ків можуть
зустрічатись однакові. Нех., нап-д, р1
зустрічається
![]() раз,
раз,
![]() раз,
…,
раз,
…,
![]() раз,
тоді розклад числа п
на прості числа мн-ки можна запис.
раз,
тоді розклад числа п
на прості числа мн-ки можна запис.![]() .
(*)
.
(*)
Мн-ки
![]() переважно розміщуються в порядку
зростання. Перетворення N
числа п
до виду
(*) наз. факторизацією
числа, а сама форма (*) – канонічною
переважно розміщуються в порядку
зростання. Перетворення N
числа п
до виду
(*) наз. факторизацією
числа, а сама форма (*) – канонічною
5. Знаходження оберненої матриці за допомогою визначників
Лема. Сума добутків ел-тів деякого рядка(стовпця) квадратної матриці на алгебраїчне доповнення відповідних ел-тів іншого рядка(стовпця) = нулю.
Дов. Нех.
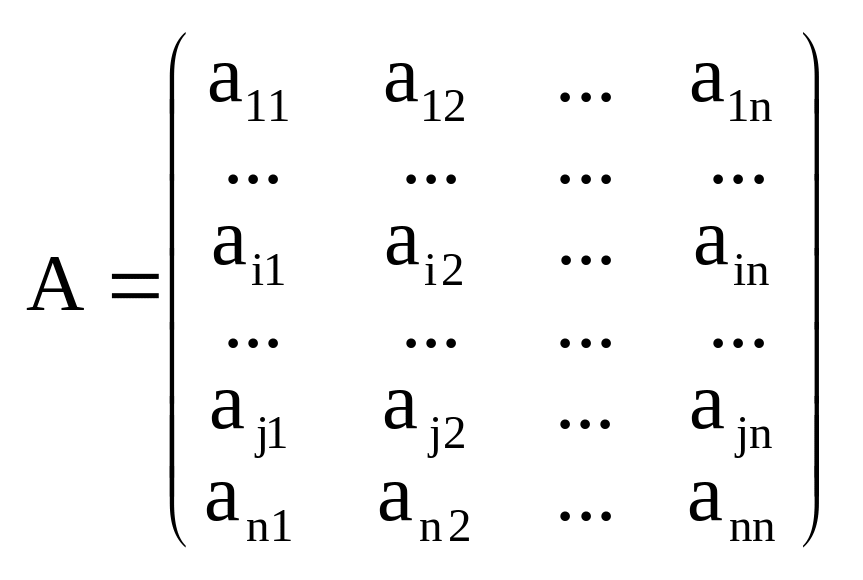
Покажемо, що
![]() ,
(
,
(![]() )
)
Розгл. матрицю В, яка відрізняється від А лише і-им рядком, тим що в i–му рядку записані ел-ти j–го рядка.
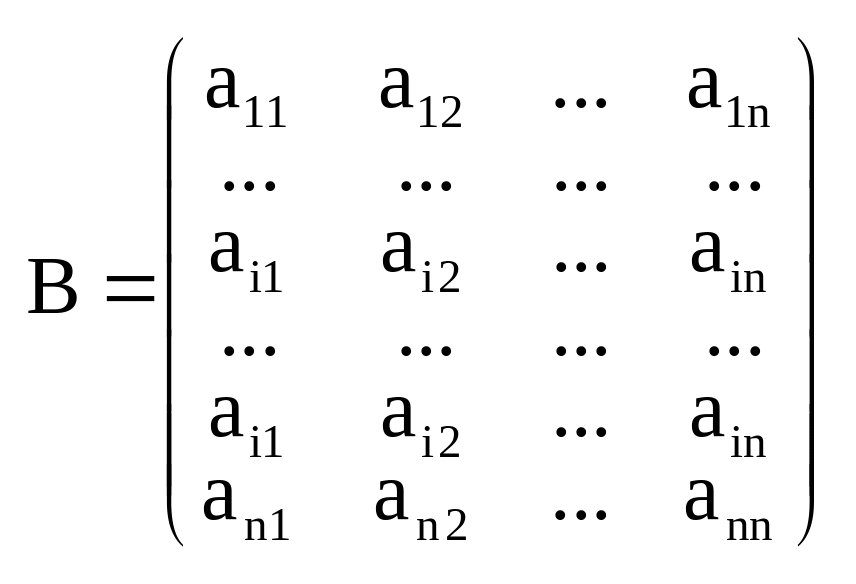 оск.
В
має 2 однакові рядки, то
оск.
В
має 2 однакові рядки, то
![]()
Розгл. визначник матриці В за j–им рядком.
![]()
![]() ,
(
)
,
(
)
Отже,
![]()
Т. Якщо
![]() – не вироджена матриця, то
– не вироджена матриця, то
![]() (*)
(*)
Дов.
Покажемо, що
![]() .
А – невироджена Þ
А–оборотна Þ
$
.
А – невироджена Þ
А–оборотна Þ
$![]() :
:![]() Þ
Þ
![]() .
Покажемо, що матриця (*) задов. рівність:
.
Покажемо, що матриця (*) задов. рівність:
![]()
![]()
![]()
![]()
![]()
![]()
Аналогічно можна показати, що Е.
Отже, є оберненою до А.
6.Розв’язування с-ми лінійних рівнянь (слр) матричним способом. Формули Крамера.
Розгл. квадратну
с-му n–рівнянь
з n
невідомими
записаному в матричній формі
![]() ,
де
–
невироджена матриця.
,
де
–
невироджена матриця.
![]() ,
,
![]() тоді, для А
тоді, для А
![]()
![]() –
формула для
знаходження розв’язків.
–
формула для
знаходження розв’язків.
Останню рівність запишемо розгорнуто
![]()
![]()
де
![]() ,
,![]()
![]() ,
,
![]() можна записати в розширеному вигляді
можна записати в розширеному вигляді
![]()
Якщо останній
![]() розкрити по і-му
стовпчику, то вийде:
розкрити по і-му
стовпчику, то вийде:
![]() Отже,
– це визначник матриці утвореної з
матриці А
заміною і-го
стовпчика стовпцем вільних членів
Отже,
– це визначник матриці утвореної з
матриці А
заміною і-го
стовпчика стовпцем вільних членів
![]() – називають формулою Крамера.
– називають формулою Крамера.
