1.1.4. Среднее и дисперсия выборки.

Допустим, что проводя экспериментальные исследования, мы сумели учесть все систематические ошибки и избежать грубых ошибок. Это значит, что истинный результат, который теоретически может быть получен при бесконечно большом числе опытов совпадает с математическим ожиданием исследуемой случайной величины, которое нам неизвестно. Для оценки неизвестного распределения генеральной совокупности случайной величины используем конечнозначную случайную (экспериментальную) величину .

Полученные в результате экспериментов числа называют элементами выборки. Каждому элементу соответствует вероятность , т.е. имеет равномерное распределение. Тогда ее математическое ожидание есть просто среднее арифметическое элементов выборки:

.

Данную количественную характеристику распределения называют простым средним выборки. Она характеризует центр группирования всей выборки и является выборочной оценкой математического ожидания генеральной совокупности исследуемой случайной величины. Точность среднего выборки будет тем выше, чем больше объем выборки.

Действие различных случайных факторов на условия проведения экспериментов порождает погрешность и приводит к превращению истинного результата в случайную величину. Следовательно, точность найденного истинного результата связана в первую очередь с мерой рассеяния - дисперсией наблюдаемой случайной величины.

Генеральную дисперсию оценивают выборочной дисперсией

.

Более детальный анализ дисперсии показывает, что истинный результат наблюдений над ней, как над случайной величиной, не совпадает с генеральной дисперсией , а оказывается несколько меньше последней. В связи с этим называется смещенной оценкой генеральной дисперсии . Несмещенной выборочной оценкой является величина

.

Переход к несмещенной оценке важен в основном для малых выборок, ибо разница между и при больших незаметна. Однако во избежание разногласий, мы в дальнейшем под выборочной дисперсией будем понимать только .

Используя знак  для обозначения суммы по всем элементам выборки, получим удобные сокращенные формулы простого среднего и дисперсии выборки

; . (1.1)

Формула расчета простого среднего применяется в случае, если частные значения усредняемого признака не повторяются или их повтор не оценивается.

В практических вычислениях для дисперсии часто удобна формула

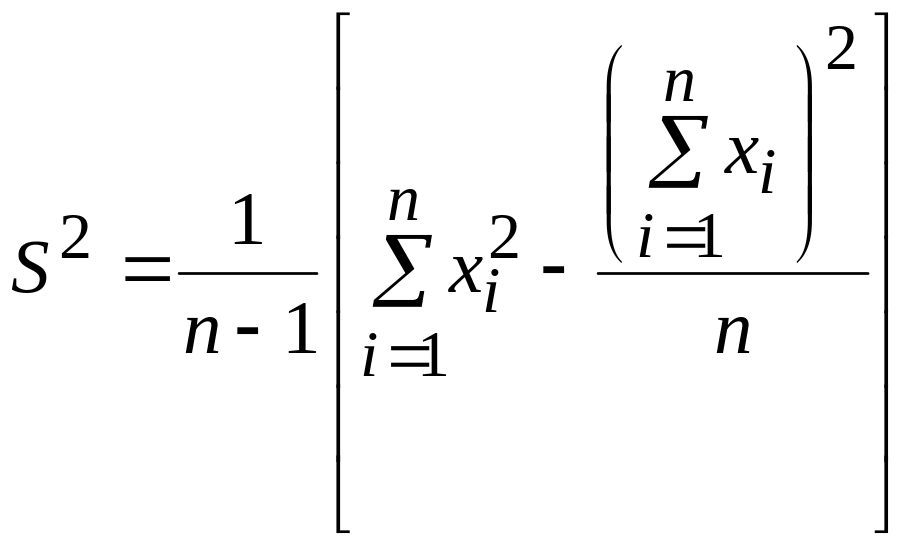. (1.2)

Величина (корень квадратный из дисперсии) называется средним квадратическим отклонением выборки или выборочным стандартом (для нормального распределения).

Таким образом, такие количественные характеристики выборки, как выборочная дисперсия или выборочное среднее квадратическое отклонение показывают разброс или характер группирования частных значений выборки относительно центра (среднего значения выборки).