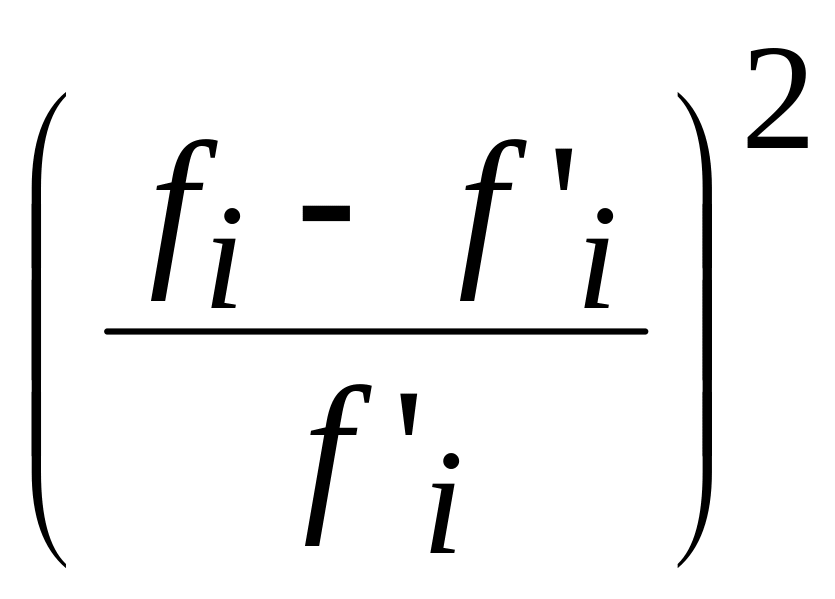- •Утверждаю
- •Одномерный статистический анализ Лекция № 1
- •Введение.
- •Генеральная совокупность значений
- •1.1.1. Погрешности (ошибки) результатов (наблюдений) при проведении исследований.
- •1.1.2. Типы выборок при использовании статистических методов управления качеством продукции.
- •Лекция № 2
- •1.1.3. Однородность и репрезентативность выборки.
- •1.1.4. Среднее и дисперсия выборки.
- •Лекция № 3
- •1.1.5. Средняя квадратическая ошибка выборки
- •1.1.6. Определение необходимой численности выборки.
- •1.1.7. Малые выборки.
- •1.2. Графическое изображение и основные характеристики вариационного ряда. Лекция № 4
- •1.2.1. Графическое изображение рядов распределения.
- •- Тарифный разряд рабочего; - число рабочих (частота).
- •Теоретической кривой нормального распределения.
- •- Тарифный разряд рабочего; - число рабочих (накопленная частота).
- •1.2.2. Основные показатели (характеристики) ряда распределения.
- •Лекция № 5
- •Относительное линейное отклонение
- •Коэффициент вариации
- •Лекция № 6
- •И отрицательным (справа) эксцессом.
- •В зависимости от расстояния от среднего значения.
- •Лекция № 7
- •Лекция № 8
- •1.3. Виды статистических оценок параметров распределения. Лекция № 9
- •1.4. Дополнительные показатели распределения:
- •Контрольные вопросы по разделу 1.
Лекция № 8
План лекции
1.2. Графическое изображение и основные характеристики вариационного ряда.
1.2.2. Основные показатели (характеристики) ряда распределения.
1.2.2.8. Критерии согласия эмпирического и теоретического
распределений.
1.2.2.8. Критерии согласия эмпирического и теоретического распределений.
Критерии согласия используют для проверки правильности выбора изученного теоретического закона для описания эмпирического распределения. Они основаны на использовании различных мер расстояний между анализируемым эмпирическим распределением и теоретической функцией распределения признака в генеральной совокупности.
Одним
из наиболее часто употребляемых критериев
согласия является критерий
«хи-квадрат» (![]() ),
предложенный К.
Пирсоном,
),
предложенный К.
Пирсоном,
![]() ,
(1.42)
,
(1.42)
где и - соответственно частоты эмпирического и теоретического распределений в -том интервале.
Чем
больше разность между наблюдаемыми и
теоретическими частотами, тем больше
расчетная величина критерия Пирсона.
Чтобы отличить
существенные (значимые) значения
от значений, которые могут возникнуть
в результате случайностей выборки,
рассчитанное значение критерия
сравнивается с табличным значением
![]() при соответствующем числе степеней
свободы и заданном уровне значимости.
Уровень значимости выбирается таким
образом, что
при соответствующем числе степеней
свободы и заданном уровне значимости.
Уровень значимости выбирается таким
образом, что
![]() (величина
(величина
![]() принимается равной 0,05 или 0,01).
принимается равной 0,05 или 0,01).
При определении значения критерия Пирсона по данным конкретной выборки, можно встретиться с такими вариантами:
1)
![]() ,
т. е.
попадает
в критическую область. Это означает,
что расхождение между теоретическими
и эмпирическими частотами существенно
и его нельзя объяснить случайными
колебаниями выборочных данных. В таком
случае гипотеза о близости эмпирического
распределения к нормальному отвергается.
,
т. е.
попадает
в критическую область. Это означает,
что расхождение между теоретическими
и эмпирическими частотами существенно
и его нельзя объяснить случайными
колебаниями выборочных данных. В таком
случае гипотеза о близости эмпирического
распределения к нормальному отвергается.
2)
![]() ,
т. е. рассчитанный критерий не превышает
максимально возможную величину
расхождений эмпирических и теоретических
частот, которая может возникнуть в силу
случайных колебаний выборочных данных.
В этом случае гипотеза о близости
эмпирического распределения к нормальному
не отвергается.
,
т. е. рассчитанный критерий не превышает
максимально возможную величину
расхождений эмпирических и теоретических
частот, которая может возникнуть в силу
случайных колебаний выборочных данных.
В этом случае гипотеза о близости
эмпирического распределения к нормальному
не отвергается.
Как уже указывалось, табличное значение критерия Пирсона определяется при фиксированном уровне значимости и соответствующем числе степеней свободы.
Число
степеней свободы равно
![]() ,
где
,
где
![]() - число условий, которые предполагаются
выполненными при вычислении теоретических
частот,
- число групп.
- число условий, которые предполагаются
выполненными при вычислении теоретических
частот,
- число групп.
Так
как при вычислении теоретических частот
нормального распределения в качестве
оценок генеральной средней и дисперсии
используются соответствующие выборочные
характеристики, то для проверки гипотезы
о нормальности распределения число
степеней свободы равно
![]() .
При расчете критерия Пирсона нужно
соблюдать следующие условия: 1) число
наблюдений должно быть достаточно
велико, во всяком случае
.
При расчете критерия Пирсона нужно
соблюдать следующие условия: 1) число
наблюдений должно быть достаточно
велико, во всяком случае
![]() ;
2) если теоретические частоты в некоторых
интервалах меньше 5, то такие интервалы
объединяют так, чтобы частоты были более
5.
;
2) если теоретические частоты в некоторых
интервалах меньше 5, то такие интервалы
объединяют так, чтобы частоты были более
5.
Воспользуемся
данными примера приведенного в табл.
1.4, для расчета критерия «хи-квадрат»,
предварительно округлив теоретические
частоты в строке 8 табл. 1.4, а также
объединив частоты двух первых и трех
последних интервалов, выполняя требование
![]() .
После таких предварительных расчетов
получают частоты эмпирического и
теоретического распределений, приведенные
в табл. 1.6. Число степеней свободы равно:
7-3=4. При уровне значимости 0,05 и числе
степеней свободы 4 значение критерия
Пирсона по соответствующей статистической
таблице определяют
.
После таких предварительных расчетов
получают частоты эмпирического и
теоретического распределений, приведенные
в табл. 1.6. Число степеней свободы равно:
7-3=4. При уровне значимости 0,05 и числе
степеней свободы 4 значение критерия
Пирсона по соответствующей статистической
таблице определяют
![]() .
.
Таблица 1.6.
Номер интервала |
Эмпирические частоты |
Теоретические частоты |
|
|
1 |
5 |
6 |
1 |
0,17 |
2 |
12 |
8 |
16 |
2,00 |
3 |
12 |
13 |
1 |
0,08 |
4 |
15 |
15 |
0 |
0,00 |
5 |
9 |
13 |
16 |
1,23 |
6 |
9 |
9 |
0 |
0,00 |
7 |
9 |
7 |
4 |
0,57 |
Итого |
71 |
71 |
|
4,05 |
![]()
Таким
образом, расчетное значение критерия
Пирсона не превышает табличного значения
при
![]() ,
т. е. проведенный расчет дает право не
отвергать гипотезу о нормальном характере
эмпирического распределения.
,
т. е. проведенный расчет дает право не
отвергать гипотезу о нормальном характере
эмпирического распределения.
Используя величину , В.И. Романовский предложил оценку близости эмпирического распределения к теоретической кривой нормального распределения производить по отношению:
![]() ,
(1.43)
,
(1.43)
где - число групп, а величина равна числу степеней свободы при вычислении частот нормального распределения. Если отношение
![]() ,
(1.44)
,
(1.44)
то расхождение частот эмпирического распределения и рассчитанных теоретических частот нормального распределения нельзя признать случайным, и гипотезу о нормальном законе распределения следует отвергнуть. Если
![]() ,
(1.45)
,
(1.45)
то возможно принять гипотезу о нормальном характере эмпирического распределения. Продолжая рассмотренный выше пример, рассчитаем критерий В.И. Романовского.
![]() .
.
Так как рассчитанное отношение значительно меньше трех, следует принять гипотезу о нормальности эмпирического распределения.
Следующий
весьма распространенный критерий
согласия – критерий
А.Н. Колмогорова.
Для определения соответствия между
теоретическим и эмпирическим
распределениями академик А.Н. Колмогоров
предложил рассматривать максимальную
разность между значениями интегральной
функции теоретического распределения
![]() и значениями интегральной функции
эмпирического распределения
.
и значениями интегральной функции
эмпирического распределения
.
Обозначим
символом
![]() абсолютную величину максимальной
разности
и
,
т. е.
абсолютную величину максимальной
разности
и
,
т. е.
![]() .
А.Н. Колмогоров установил, что когда
неограниченно возрастает, вероятность
того, что
будет меньше величины
.
А.Н. Колмогоров установил, что когда
неограниченно возрастает, вероятность
того, что
будет меньше величины
![]() ,
приближается к значениям функции.
,
приближается к значениям функции.
![]() т.
е.
т.
е.
![]() .
(1.46)
.
(1.46)
По
таблицам вероятностей
![]() можно найти величину
можно найти величину
![]() ,
соответствующую данной величине
вероятности
.
Если известен объем выборки, можно
рассчитать соотношение
.
Величина
,
рассчитанная по данным выборки,
сравнивается с величиной
.
,
соответствующую данной величине
вероятности
.
Если известен объем выборки, можно
рассчитать соотношение
.
Величина
,
рассчитанная по данным выборки,
сравнивается с величиной
.
Если
![]() ,
то с вероятностью
можно считать, что рассматриваемое
распределение соответствует нормальному
закону.
,
то с вероятностью
можно считать, что рассматриваемое
распределение соответствует нормальному
закону.
Если
же
![]() ,
то вероятность того, что гипотеза о
соответствии теоретического и
эмпирического распределений верна,
определяется величиной
,
то вероятность того, что гипотеза о
соответствии теоретического и
эмпирического распределений верна,
определяется величиной
![]() .
.
Так
как величину
выбирают равной 0,95 или 0,99, то
![]() .
В силу малой вероятности такого события
гипотеза о нормальном характере
эмпирического распределения отвергается.
.
В силу малой вероятности такого события
гипотеза о нормальном характере
эмпирического распределения отвергается.
Приведем краткую выдержку из таблицы значений функции А.Н. Колмогорова:
Таблица 1.7.
|
1,23 |
1,36 |
1,63 |
1,80 |
2,00 |
|
0,9030 |
0,9505 |
0,9902 |
0,9970 |
0,9993 |
Покажем расчет критерия А.Н. Колмогорова на рассмотренном ранее примере, результаты расчета приведены в табл. 1.8.
Таблица 1.8.
Номер интервала |
Частоты |
Частоты абсолютные накопленные |
Частоты отностельные накопленные |
|
|
|||
эмпири- ческие
|
теорети- ческие
|
эмпири- ческие
|
теорети- ческие
|
эмпири- ческие
|
теорети- ческие
|
|||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
5 |
6 |
5 |
6 |
0,0704 |
0,0845 |
0,0141 |
1 |
2 |
12 |
8 |
17 |
14 |
0,2394 |
0,1972 |
0,0422 |
3 |
3 |
12 |
13 |
29 |
27 |
0,4085 |
0,3803 |
0,0282 |
2 |
4 |
15 |
15 |
44 |
42 |
0,6197 |
0,5915 |
0,0282 |
2 |
5 |
9 |
13 |
53 |
55 |
0,7465 |
0,7746 |
0,0281 |
2 |
6 |
9 |
9 |
62 |
64 |
0,8732 |
0,9014 |
0,0282 |
2 |
7 |
9 |
7 |
71 |
71 |
1,0000 |
1,0000 |
0,0000 |
0 |
Наибольшая
по абсолютной величине разность
накопленных относительных частот
![]() соответствует (столбец 8).
соответствует (столбец 8).
Принимая
уровень значимости
,
т. е. при доверительной вероятности
![]() ,
по таблицам значений функций А.Н.
Колмогорова находим
,
по таблицам значений функций А.Н.
Колмогорова находим
![]() ,
и, следовательно, для
,
и, следовательно, для
![]() величина
равна 0,1614. Вероятность того, что
была установлена нами равной 0,05 (
величина
равна 0,1614. Вероятность того, что
была установлена нами равной 0,05 (![]() ).
Такой результат является практически
невозможным, когда проверяемая гипотеза
о соответствии эмпирического распределения
нормальному закону верна. Поскольку
величина
,
рассчитанная по данным приводимого
примера, получилась меньше величины
,
с вероятностью 95 % принимается гипотеза
о нормальности эмпирического распределения.
).
Такой результат является практически
невозможным, когда проверяемая гипотеза
о соответствии эмпирического распределения
нормальному закону верна. Поскольку
величина
,
рассчитанная по данным приводимого
примера, получилась меньше величины
,
с вероятностью 95 % принимается гипотеза
о нормальности эмпирического распределения.
Для
расчета функции
(критерия Колмогорова) можно использовать
и максимальную разность абсолютных
накопленных частот, т. е. величину
![]() .
Тогда между
.
Тогда между
![]() и
будет соотношение:
и
будет соотношение:
![]() ,
т. е.
,
т. е.
![]() .
Максимальная величина разности абсолютных
накопленных частот равна 3 (столбец 9).
Величина
,
соответствующая
.
Максимальная величина разности абсолютных
накопленных частот равна 3 (столбец 9).
Величина
,
соответствующая
![]() равна 1,36. Следовательно, для
величина
равна 1,36. Следовательно, для
величина
![]() равна 11,4594. Так как значение
равна 11,4594. Так как значение
![]() меньше
меньше
![]() ,
то можно считать, что результаты выборки
не противоречат предположению о
нормальном характере распределения
исследуемого признака.
,
то можно считать, что результаты выборки
не противоречат предположению о
нормальном характере распределения
исследуемого признака.