И отрицательным (справа) эксцессом.

На рисунке 1.5 представлены два распределения: одно – островершинное (величина эксцесса положительная), второе – плосковершинное (величина эксцесса отрицательная).

Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения.

В нормальном распределении отношение . Средняя квадратическая ошибка эксцесса рассчитывается по формуле:

, (1.24)

где - число наблюдений (опытов).

1.2.2.4. Нормальный закон распределения.

Если непрерывная случайная величина имеет:

- функцию распределения

. (1.25)

- плотность распределения, являющаяся производной от функции распределения

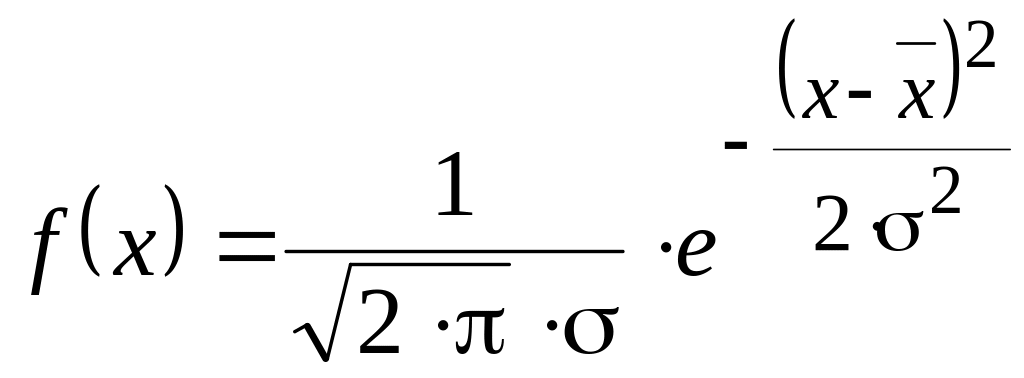, (1.26)

то она подчиняется нормальному закону распределения. Дисперсия и среднее квадратическое отклонение (стандарт) при нормальном законе распределения имеют свое обозначение соответственно и . Для построения кривой нормального распределения достаточно знать два параметра и .

По формуле Ньютона – Лейбница можно определить вероятность попадания частного значения исследуемого признака в заданный интервал нормального распределения

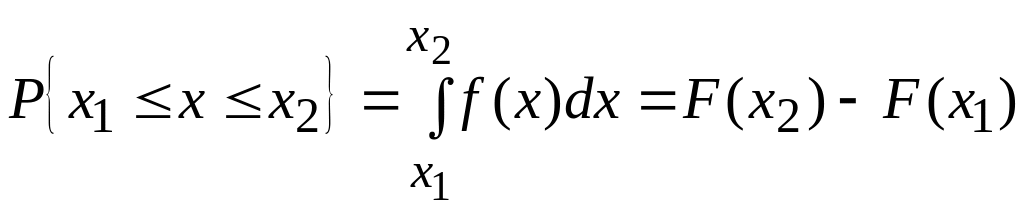, (1.27)

где и - значения функции Лапласа на границах интервала.

При группировании всех частных значений совокупности (выборки) в интервалы о вероятности попадания определенного количества частных значений в тот или иной интервал говорят как о теоретической частоте такого попадания.

Значение функции распределения для границ интервала можно определить по готовым таблицам, уже составленным для нормального распределения. Однако табулирование функции наталкивается на одну трудность - для каждых конкретных значений и нужно составлять свою таблицу. Этой трудности удается избежать, приводя все нормальные распределения к такому распределению, у которого и . Нормальное распределение с такими параметрами называется стандартным. Эти значения легко найти в статистических справочниках, где они табулированы в соответствующих таблицах.

Укажем особенности кривой нормального распределения.

1. Кривая симметрична относительно максимальной ординаты. Максимальная ордината соответствует значению признака 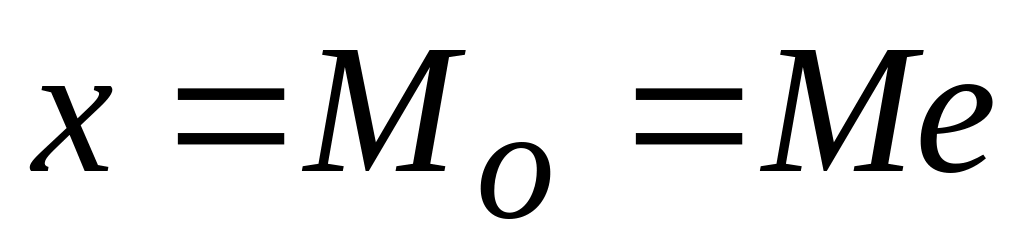, ее величина равна .

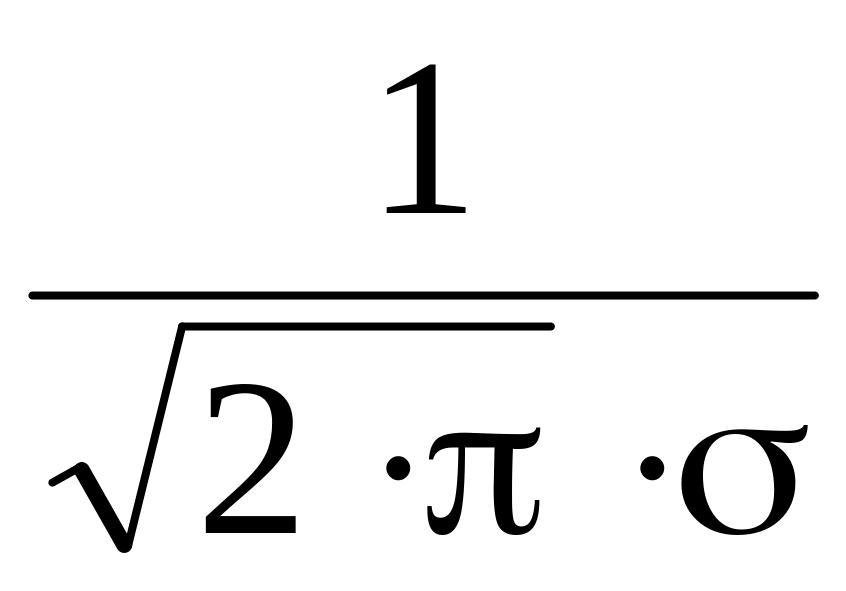2. Кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности. Следовательно, чем больше частные значения отклоняются от , тем реже они встречаются. Одинаковые по абсолютному значению, но противоположные по знаку отклонения значений переменной от равновероятны.

3. Кривая имеет две точки перегиба, находящиеся на расстоянии 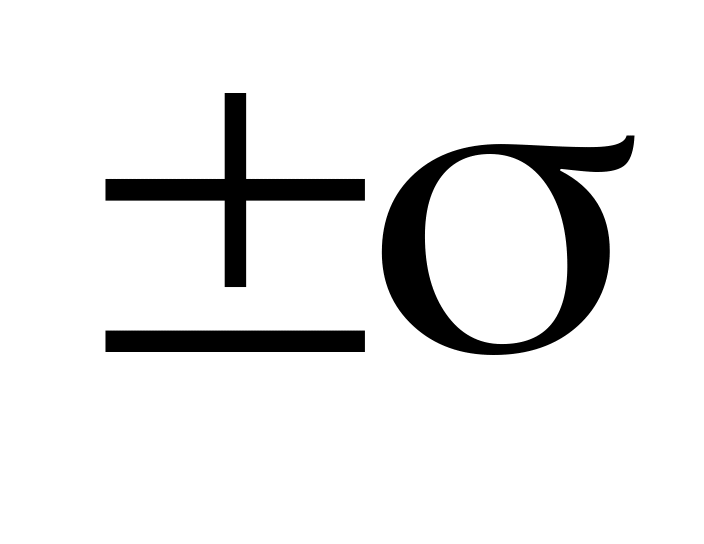от .

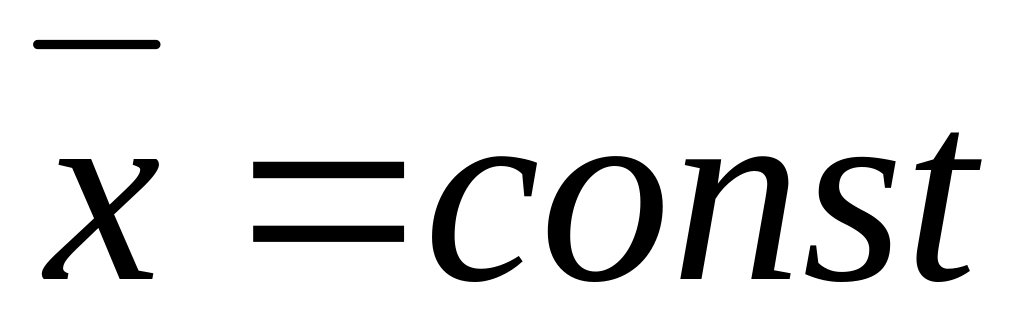4. При с увеличением кривая становится более пологой. При 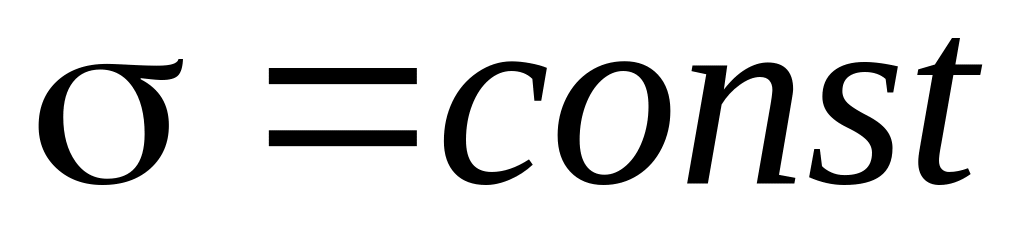с изменением кривая не меняет свою форму, а лишь сдвигается вправо или влево по оси абсцисс.

5. Вероятность попадания частного значения исследуемого признака в заданный интервал можно приближенно оценивать по следующим правилам (п.1.1.6):

- в промежутке находится 68,3 % всех значений признака (правило «сигмы»);

- в промежутке находится 95,4 % всех значений признака (правило «двух сигм»);

- в промежутке находится 99,7 % всех значений признака (правило «трех сигм»). Как отмечалось ранее, в соответствии с правилом «трех сигм» попадание частного значения в данный интервал практически гарантирован (рис. 1.6).

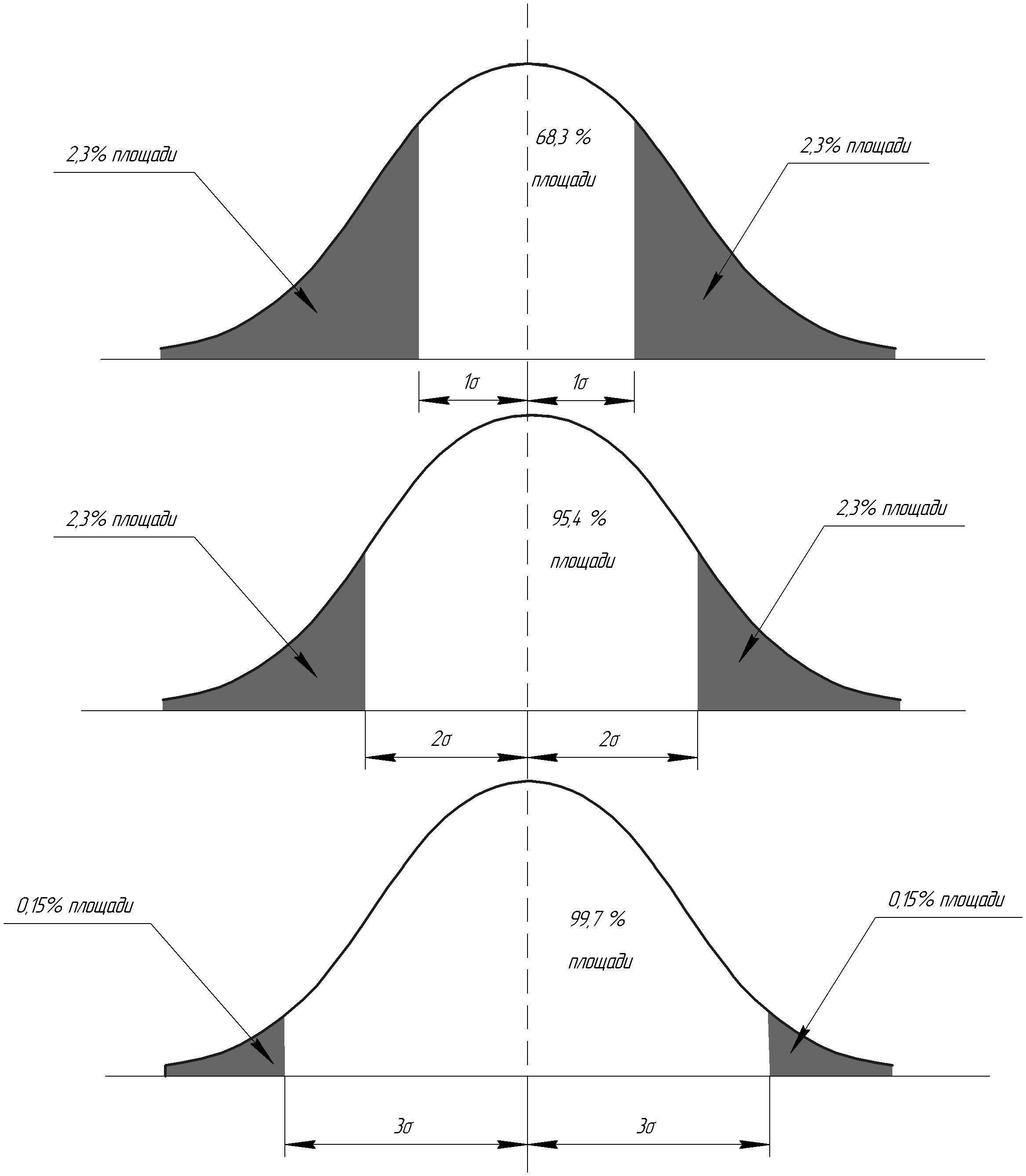
Рис. 1.6. Соотношение площади под кривой нормального распределения