В зависимости от расстояния от среднего значения.

Нормальное распределение возможно в том случае, когда на величину признака влияет большое число случайных величин. Действие случайных величин независимо, и ни одна них не имеет преобладающего влияния над другими.

1.2.2.5. Выравнивание эмпирического распределения по нормальному закону (построение теоретической нормальной кривой распределения).

Выравнивание эмпирического распределения по нормальному закону проводится в рамках проверки гипотезы о принимаемом известном законе полученного эмпирического распределения.

Для удобства вычислений частные значения исследуемого признака нормируются, а затем используются заранее табулированные значения плотности функции распределения нормированной случайной величины. В случае группировки данных нормируются значения середин интервалов. Как отмечалось ранее под нормированием понимают приведение произвольного нормального распределения с вычисленными параметрами и к стандартному распределению с параметрами и .

Если обозначить

, (1.28)

то величина , называемая нормированной функцией нормального распределения (1.25), определяется по зависимости

. (1.29)

Определенный интеграл вида

(1.30)

называется нормированной функцией Лапласа (1.26), которая также табулирована в статистических таблицах и используется во многих статистических расчетах и, в частности, при выравнивании статистических распределений.

При выравнивании эмпирического распределения под вероятностью попадания исследуемого признака в заданный интервал также понимают теоретическую частоту попадания частных значений исследуемого признака в какой-либо интервал, на которые разбит общий интервал выборки.

Поскольку между частными значениями нормированной и ненормированной функций Лапласа существует соотношение , то легко показать, что соотношение (1.27) приводится к виду

, (1.31)

то есть для определения вероятности попадания исследуемого признака в заданный интервал или теоретической частоты при группировании для любого нормального распределения достаточно установить разность между значениями нормированной функции Лапласа на границах интервала.

Если какое - нибудь из заданных значений , отрицательно, то для нее функцию Лапласа вычисляют с использованием свойств нечетности.

Применительно к выравниванию эмпирического нормального распределения процедура расчета теоретических интервальных частот выглядит следующим образом:

1. Из предварительного анализа полученного эмпирического распределения известны рассчитанные значения эмпирических интервальных частот , количественные параметры эмпирического распределения в целом: , .

2. Верхние и нижние 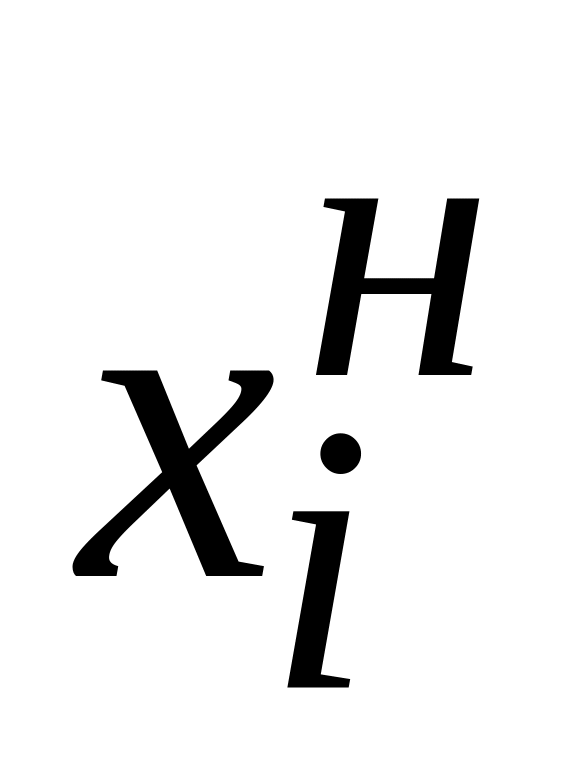границы каждого интервала нормируются по формуле (1.28)

. (1.32)

3. По рассчитанным нормированным границам интервалов с помощью статистических таблиц значений функции Лапласа для различных нормированных аргументов (например, ) находят соответствующие значения функции Лапласа для границ интервалов 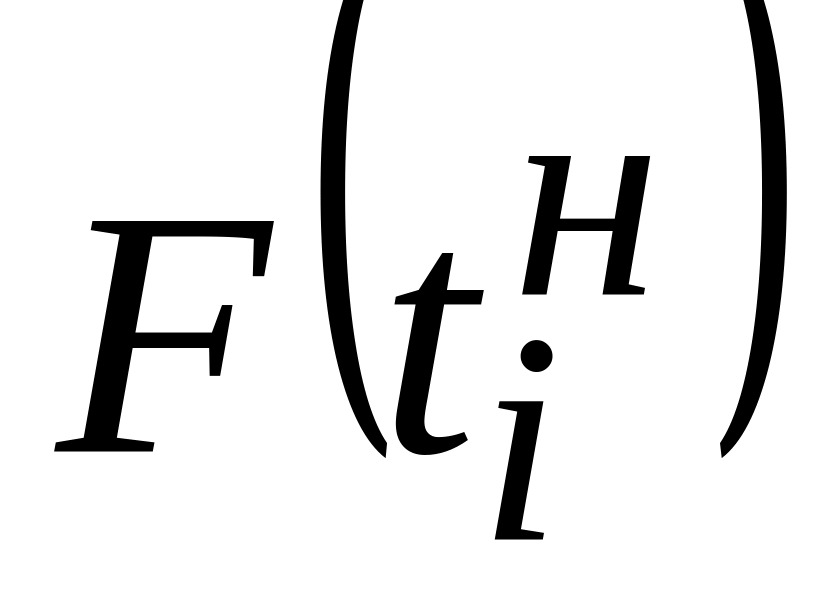и .

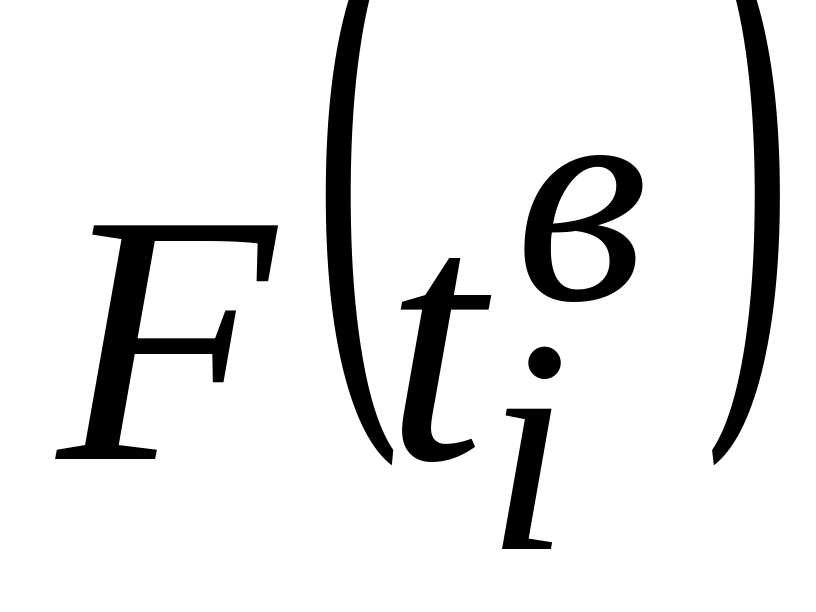4. По зависимости (1.31) оценивают теоретическую вероятность 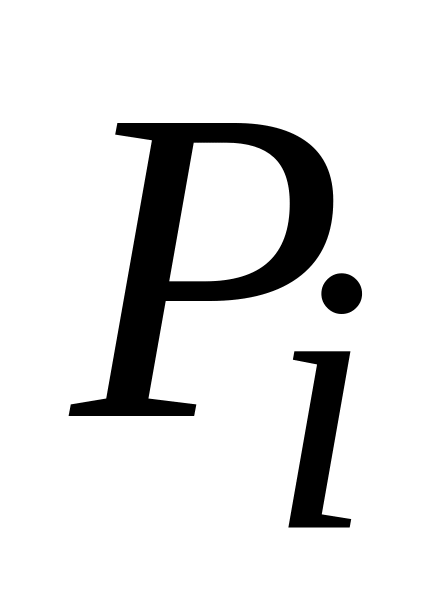попадания исследуемого признака в соответствующий интервал (как разность значений функций Лапласа для границ интервала) для всех интервалов

. (1.33)

5. Теоретические частоты 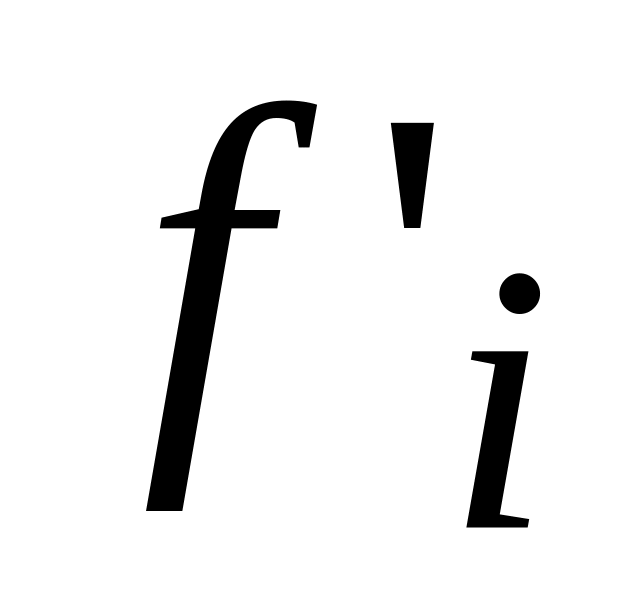рассчитывают умножением интервальной теоретической вероятности на общий объем выборки

(1.34)

1.2.2.6. Примеры вычисления вероятностей попадания случайной величины в заданный интервал. Задача об абсолютном отклонении.

ПРИМЕР 1. Найти вероятность того, что нормированная случайная величина примет значение между - 1 и 1/2.

Согласно общей формуле (1.31)

.

По таблице значений функции Лапласа находим, что . Если значение в таблице отсутствует, то используют свойство нечетности функции Ф(-1) = - Ф(1) = - 0,3413.

Вычисления еще более упрощаются, если числа и симметричны относительно среднего значения . С такой ситуацией приходится сталкиваться в задаче об абсолютном отклонении. Абсолютным отклонением называется разность между случайной величиной и ее математическим ожиданием, взятая по абсолютной величине:

. (1.35)

Задача об абсолютном отклонении звучит так: найти вероятность того, что абсолютное отклонение случайной величины не превзойдет некоторого заданного числа . Эта задача сводится к уже рассмотренной, т.к. неравенство равносильно неравенствам .

. (1.36)

В частности для нормированной случайной величины (1.33)

. (1.37)

Учитывая нечетность функции Лапласа , получим очень важную для приложений формулу

. (1.38)

Для ненормированной случайной величины задача об абсолютном отклонении определяется выражением

. (1.39)

ПРИМЕР 2. Случайная величина имеет нормальное распределение с параметрами и . Какова вероятность того, что она примет значение, лежащее между 15 и 40.

Используя формулу (1.33) и таблицу значений функции Лапласа, находим (форма записи при отсутствии интервалов):

.

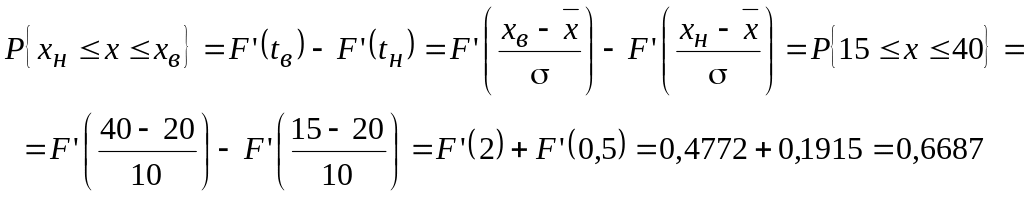ПРИМЕР 3. Детали, изготавливаемые на станке, в силу различных случайных причин отличаются по своему диаметру. Удалось установить, что диаметр есть нормально распределенная случайная величина со стандартом  = 2 мм. Какова вероятность брака, если бракуются детали, диаметр которых симметрично отклоняется от номинала (математического ожидания) более, чем на 3,5 мм .

По условиям задачи требуется найти вероятность неравенства . Мы такого неравенства не рассматривали, поэтому перейдем к противоположному событию, т.е. неравенству . Полагая и учитывая, что , найдем по зависимости (1.38)

.

Значит вероятность противоположного события определится по формуле

.

Как видно из (1.37), в задаче об абсолютном отклонении математическое ожидание случайной величины не играет ни какой роли - достаточно знать лишь стандарт  или дисперсию ². Мы пришли к следующему важному правилу: вероятность того, что абсолютное отклонение нормально распределенной случайной величины не превзойдет некоторого предела, зависит только от того, во сколько раз этот предел больше стандарта рассматриваемой случайной величины. Отсюда, кстати, ясно и происхождение названия «стандарт» - это величина с которой сравнивают все отклонения.