5.1.2.4. Аппроксимация сложных пространственных поверхностей, задаваемых координатами опорных точек

Для аппроксимации сложных пространственных поверхностей, задаваемых координатами опорных точек поверхности, целесообразно применять многомерные полиномы. В отличие от описания поверхности сплайн–функциями данный метод позволяет исключить колебательный процесс, который возникает в результате совпадения точек поверхности в опорных точках и отсутствия гладкости полученного описания в промежутках между опорными точками поверхности. В данном случае аппроксимация поверхности между двумя точками основывается на знании координат опорной точки и частных производных в данной точке. Это не накладывает требований на гладкость поверхности между опорными точками.

При описании гладких поверхностей полиномами необходимо знать координаты предыдущих и последующих опорных точек поверхности. В этом случае обеспечивается сглаживание поверхности между опорными точками. Рассмотрим применение для этих целей многомерных полиномов Лагранжа, зависимых от двух переменных. Метод сопровождающего трехгранника, рассмотренный выше для описания поверхностей, в сочетании с полиномами Лагранжа дает возможность планировать траекторию перемещения инструмента относительно детали и формировать управление манипуляторами для поверхностей, задаваемых координатами опорных точек.

Описание поверхности полиномами состоит в последовательном решении следующих задач:

1. Приближенное описание поверхности полиномами по заданным координатам опорных точек поверхности в системе координат (XYZ)_д.

2. Определение ориентации сопровождающего трехгранника (τνβ)_i относительно осей системы координат (XYZ)_д.

3. Нахождение элементов матрицы, определяющей закон перемещения инструмента относительно детали.

Задача 1

Задача 1 состоит в получении коэффициентов полиномов Лагранжа по заданным координатам опорных точек поверхности. Интерполяционные полиномы Лагранжа одной переменной позволяют аппроксимировать функцию y=f(x) в системе координат детали (XYZ)_д, задаваемую координатами опорных точек (x_i,y_i)

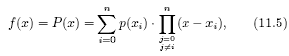
где коэффициенты полиномов Лагранжа p(x_i) определяются через значения x_i, y_i в опорных точках

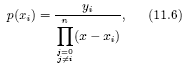
где i=0÷n, j=0÷n, n — степень полинома.

Полином Лагранжа двух переменных для поверхности, представленной на рис. 4, по аналогии с полиномом одной переменной имеет вид

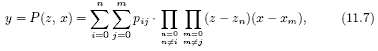
где i=[0÷n] — количество опорных сечений поверхности вдоль оси X_д; j=[0÷n] — количество опорных сечений поверхности вдоль оси Z_д; p_ij — коэффициенты полинома, определяемые через координаты опорных точек поверхности.

Рассмотрим аппроксимацию поверхности полиномами Лагранжа второй степени.

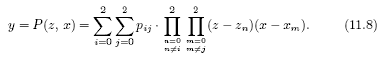
При интерполяции поверхности полиномами двух переменных необходимо, чтобы опорные точки поверхности (узлы интерполяции) образовывали сетку. Наиболее удобной является прямоугольная сетка с равномерным распределением клеток. В этом случае поверхность, представляемая координатами узлов прямоугольной сетки (рис. 5 а), в зависимости от расположения текущих координат (z,x) поверхности последовательно "накрывается" прямоугольником (рис. 5 б). При этом для более точной аппроксимации необходимо, чтобы текущие координаты поверхности (z,x) находились в области центра прямоугольника, ограниченного координатами

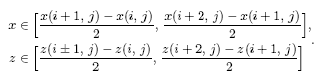
Последовательность выбора опорных точек, описывающих заданную ограниченную область поверхности, где проходит планируемая траектория, состоит в том, что все последующие опорные точки поверхности выбираются только после выхода i–й точки планируемой траектории из центра прямоугольника (рис. 5 б).

Постоянные коэффициенты полинома p_ij (11.8) определяются для каждого элемента поверхности через координаты известных опорных точек поверхности

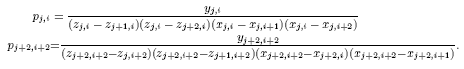
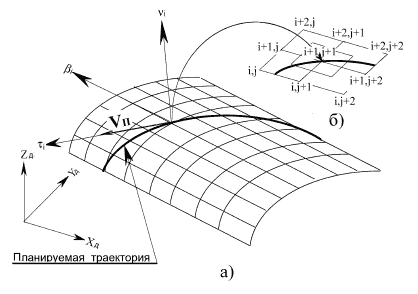
Рис. 5.

С учетом принятых обозначений полином (11.8) приводится к виду

y=a₁z²x²+a₂z²x+a₃zx²+a₄z²+a₅x²+a₆zx+a₇z+a₈x+a₉, (11.9)

где коэффициенты a_k вычисляются через постоянные p_ij и координаты опорных точек поверхности.

Задача 2

Задача 2 состоит в определении углов ориентации трехгранника (τνβ)_i относительно осей системы координат (XYZ)_д. Для каждой i–й точки поверхности, используя уравнение (11.9), кроме текущих координат поверхности, вычисляются направляющие косинусы для осей трехгранника (τνβ)_i, связанного с поверхностью, которые представляют соответственно касательную, нормаль и бинормаль в каждой точке поверхности.

Для нахождения углов ориентации сопровождающего трехгранника (τνβ)_i в каждой точке траектории относительно осей системы координат (XYZ)_д необходимо получить уравнение нормали в точке поверхности, касательной к траектории перемещения инструмента относительно детали, и уравнение бинормали.

Направляющие косинусы нормали (ось ν_i) к поверхности в каждой точке траектории x_iy_iz_i определяются из уравнения (11.9)

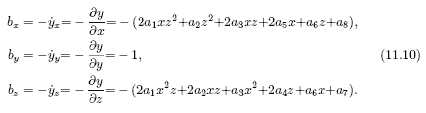
С учетом (11.10) направляющие косинусы для оси ν_i в точке поверхности относительно осей системы координат (XYZ)_д принимают вид

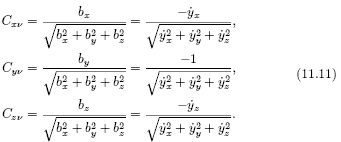
Направляющие косинусы для касательной (ось τ_i) к траектории движения инструмента относительно детали определяется через частные производные от x, y, z по времени в i–й точке

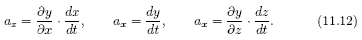
С учетом (11.12) получим

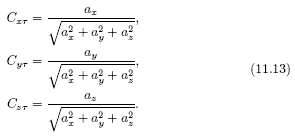
Направляющие косинусы для бинормали трехгранника (τνβ)_i — (ось β_i) определяются из векторного произведения

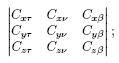
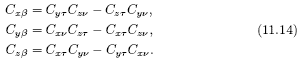
Таким образом, уравнения (11.11), (11.13) и (11.14) определяют ориентацию подвижного трехгранника (τνβ)_i относительно осей системы координат (XYZ)_д.