
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Билет №12
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Билет №14
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Билет №16
- •Вопрос 1
- •Вопрос 3
Билет №14
Вопрос 1
Частные производные функции двух переменных и правило их вычисления
Частные
производные первого порядка. Пусть
функция ![]() определена
в области
определена
в области ![]() и
и ![]() .
Тогда при малых
.
Тогда при малых ![]() определено
ее частное приращение по
определено
ее частное приращение по ![]() :
: ![]() .
.
Определение. Частной
производной функции ![]() по
переменной
в
точке
по
переменной
в
точке ![]() называют
предел
называют
предел
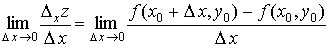 ,
,
если он существует.
Частную производную по обозначают одним из следующих символов:
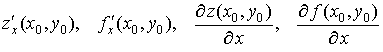 .
.
Аналогично
определяется частная производная по ![]() и
вводятся ее обозначения.
и
вводятся ее обозначения.
Легко видеть, что частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Поэтому частные производные вычисляются по тем же правилам, что и вычисление производных функций одной переменной
Вопрос 3
Неопределенный интеграл и его свойства
Определение первообразной и неопределенного интеграла
Функция F(x) называется первообразной функции f(x), если
Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функции f(x) и обозначается как
Таким образом, если F - некоторая частная первообразная, то справедливо выражение
где С - произвольная постоянная. Свойства неопределенного интеграла
В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f, а, k, C - постоянные величины.
БИЛЕТ №15
Вопрос 1
Частные производные второго порядка
Пусть
функция
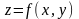 определена в некоторой области
определена в некоторой области
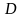 .
Если функция
имеет частные производные
.
Если функция
имеет частные производные
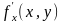 и
и
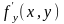 ,
то они в общем случае тоже будут
функциями двух переменных
,
то они в общем случае тоже будут
функциями двух переменных
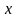 и
и
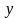 ,
определенных в области
или ее части. Будем называть в дальнейшем
функции
и
частными производными первого порядка
(или просто первыми частными
производными) функции
,
определенных в области
или ее части. Будем называть в дальнейшем
функции
и
частными производными первого порядка
(или просто первыми частными
производными) функции
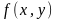 .
Частные производные по
и по
от функций
и
,
если они существуют, называются частными
производными второго порядка (вторыми
частными производными) функции
.
Обозначают частные производные второго
порядка функции
следующим образом:
.
Частные производные по
и по
от функций
и
,
если они существуют, называются частными
производными второго порядка (вторыми
частными производными) функции
.
Обозначают частные производные второго
порядка функции
следующим образом:
1) производная по от функции обозначается одним из следующих символов
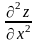 ,
,
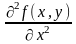 ,
,
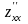 ,
,
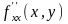 ;
;
2) производная по от функции обозначается
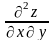 ,
,
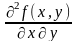 ,
,
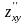 ,
,
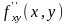 ;
;
4) производная по от обозначается
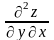 ,
,
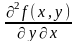 ,
,
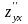 ,
,
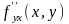 ;
;
5) производная по от обозначается
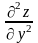 ,
,
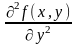 ,
,
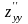 ,
,
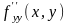 .
.
Вопрос 3
Дифференциальное уравнение первого порядка с разделяющимися переменными
Дифференциальное уравнение вида
или
называется дифференциальным уравнением с разделяющимися переменными.
Заметим, что в данных дифференциальных уравнениях каждая из функций зависит только от одной переменной, т.е. происходит разделение переменных.
Для решения такого дифференциального уравнения необходимо домножить или разделить обе части дифференциального уравнения на такое выражение, чтобы в одну часть уравнения входили только функции от и , в другую часть уравнения - только функции от y, dy . Затем в полученном дифференциальном уравнении надо проинтегрировать обе части:
Следует заметить, что при делении обеих частей дифференциального уравнения на выражение, содержащее неизвестные x и y, могут быть потеряны решения, обращающие это выражение в ноль. Обратим внимание, что
дифференциальные уравнения с разделяющимися переменными легко сводятся к интегрированию. В общем случае получаем два неопределенных интеграла
