Билет №12

Вопрос 1

Понятие функции двух переменных, ее области определения.

Закон (правило) по которому каждой паре (х,у)є D независимых переменных ставиться в соответствие определенное значение z = f(х, у) є G называется функцией двух переменных. Совокупность пар (х,у) є D значений х и у, при которых функция z = f(х, v) имеет смысл, называется областью определения функции.

Вопрос 3

Дифференциальное уравнение второго порядка, допускающее понижение порядка

Уравнение вида у” = f(x) называется дифференциальным уравнением второго порядка, допускающим понижения порядка. Чтобы понизить порядок уравнения запишем его в виде: dy’/dx=f(х), откуда dy’=f(x)dx, интегрируя получим у’=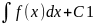 уравнение 1-го порядка. Еще раз проинтегрировав его, получим искомое решение у=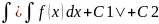

БИЛЕТ №13

Вопрос 1

Полное и частное приращение функции двух переменных

Приращение, которое получает функция Z=f(x, y), когда изменяется только одна из переменных, называется частным приращением функции по соответствующей переменной: Δ_xZ=f(x+Δx,y)-f(x,y), Δ_yZ=f(x,y+Δy)-f(x,y).

ОПРЕДЕЛЕНИЕ: Частным дифференциалом по х функции Z=f(x, y) называется главная часть частного приращения ΔxZ=f(x+Δx,y)-f(x,y), пропорциональная приращению Δx независимой переменной х. Аналогично определяется частный дифференциал по у, т.е. ΔyZ=f(y+Δy,x)-f(x,y).

Дифференциалы независимых переменных х и у просто равны их приращениям, т.е. dx=Δx, dy=Δy. Частные дифференциалы обозначаются так: dxZ -частный дифференциал по х, dyZ - частный дифференциал по у. При этом:

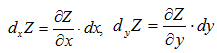
Таким образом, частный дифференциал функции двух независимых переменных равен произведению соответствующей частной производной на дифференциал этой переменной.

Таким же образом, как для функции двух переменных, определяются частные приращения и частные дифференциалы функций любого числа независимых переменных.

Приращение, которое получает функция Z=f(x,y) при произвольных совместных изменениях ее обоих аргументов называется полным приращением:

ΔZ=f(x+Δx,y+Δy)-f(x,y)

ОПРЕДЕЛЕНИЕ: Полным дифференциалом функции двух переменных называется главная часть полного приращения функции, линейная относительно приращений независимых переменных.

Теорема. Полный дифференциал функции двух независимых переменных равен сумме произведений частных производных функции на дифференциалы соответствующих независимых переменных.

dZ=f'x(x,y)dx+f'y(x,y)dy или 

Так как  dx=dxZ и  dy=dyZ, то dZ=dxZ+dyZ, т.е. дифференциал функции двух независимых переменных равен сумме ее частных дифференциалов.

Определение дифференциала переносится на функции любого числа независимых переменных.

Вопрос 3

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Дифференциальные уравнения вида ay′′ + by′ +cy = 0, где a, b, c – числа, называют линейными однородными дифференциальными уравнениями 2-го порядка с постоянными коэффициентами.

Решение таких уравнений осуществляется по следующей схеме:

1. Сначала решается квадратное уравнение a λ² +b λ+ c = 0 ,

которое называют характеристическим уравнением для исходного дифференциального уравнения.

2. Если характеристическое уравнение имеет два различных вещественных корня

λ₁ и λ₂ , то общее решение исходного дифференциального уравнения имеет вид

y=C₁e^λ1x + C₂e^λ2x ,где C₁ и С₂ – произвольные числа.

3. Если характеристическое уравнение имеет два совпавших вещественных корня

λ₁ =λ₂= λ , то общее решение исходного дифференциального уравнения имеет вид

y=e^λx(C₁+C₂x), где C₁ и С₂ – произвольные числа.

3. Если характеристическое уравнение имеет два комплексно-сопряженных корня

λ₁= α+jβ и λ₂= α - jβ, то общее решение исходного дифференциального уравнения имеет вид y=e^αx(C₁sinβx+C₂cosβx) , где C₁ и С₂ – произвольные числа.

• Линейное однородное дифференциальное уравнение 2-го порядка с

постоянными коэффициентами y ′′ + ω²y = 0, где ω ≠ 0 – вещественное число, называют уравнением гармонических колебаний. Общее решение этого уравнения имеет вид

y=C₁sin ωx+C₂cos ωx), где C₁ и С₂ – произвольные числа. Число ω называют частотой гармонических колебаний.