4.35. Теорема о вычетах. Вычисление интегралов с помощью вычетов
Теорема. Пусть функция f(z) – аналитическая на всей плоскости z, за исключением конечного числа точек z1, z2, …, zN. Тогда верно равенство:
А интеграл от функции по контуру L, содержащему внутри себя эти точки, равен
Эти свойства применяются для вычисления интегралов. Если функция f(z) аналитическая в верхней полуплоскости, включая действительную ось, за исключением N точек, то справедлива формула
Пример.
Вычислить определенный интеграл
.
Подынтегральная функция является аналитической в верхней полуплоскости за исключением точки 2i. Эта точка является полюсом второго порядка.
Найдем вычет
функции
Получаем
Пример.
Вычислить определенный интеграл
Подынтегральная функция является аналитической в верхней полуплоскости за исключением точки i. Эта точка является полюсом второго порядка.
Найдем вычет функции
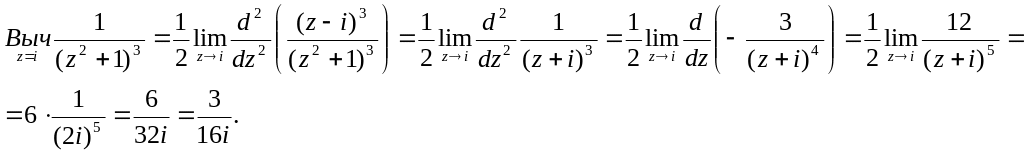
Получаем
Образцы решения типовых заданий
ПРИМЕР 1. Найдите предел
Решение.
Разделим числитель и знаменатель выражения на 7n. После преобразований получим:
.
(Так как при
выражение
стремится к нулю по свойству показательной
функции с основанием 0<a<1).
ПРИМЕР 2. Найдите предел
Решение.
Имеем неопределённость вида
.
Чтобы устранить её, разделим числитель
и знаменатель на
:
.
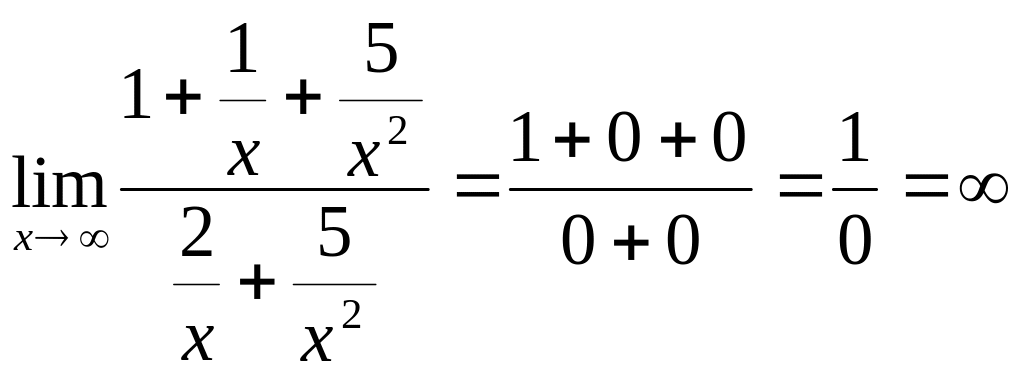ПРИМЕР 3. Найдите предел
.
Решение.
Имеем неопределённость вида
.
Чтобы раскрыть её, умножим и разделим
выражение в скобках на сопряженное ему
выражение
.
Получим:
.
ПРИМЕР 4. Найти предел
Решение.
Имеем неопределенность вида “0/0”. Подвергнем функцию преобразованию, чтобы получить возможность использовать первый замечательный предел;
.
ПРИМЕР 5. Найти предел
.
Решение.
Имеем неопределённость вида
.
Чтобы воспользоваться вторым замечательным
пределом, преобразуем данную функцию:
.
ПРИМЕР 6. Продифференцировать функцию:
.
Решение.
Находим производную данной функции по правилам дифференцирования сложной функции:
ПРИМЕР 7. Найти производную функции,
заданной неявно:
.
Решение.
Дифференцируем данную функцию по х:
,
откуда
ПРИМЕР 8. Найти производную
от функции, заданной параметрически:
.
Решение.
.
ПРИМЕР 9. Найти область определения
функции
Решение.
Данная функция определена для всех х,
не обращающих в нуль знаменатель, т.е.
не являющихся корнями уравнения
.
Это все числа вида
.
Таким образом, область определения D(у) - вся числовая прямая, кроме точек .
ПРИМЕР 10. Исследовать функцию и построить
ее график:
Решение.
Функция определена и непрерывна в
интервале (0;+). В
граничной точке
области определения функция имеет
бесконечный разрыв, так как
.
Так как в точке
функция имеет бесконечный разрыв, то
прямая
является вертикальной асимптотой.
Найдем уравнение наклонной асимптоты
(если
она существует).
;
.
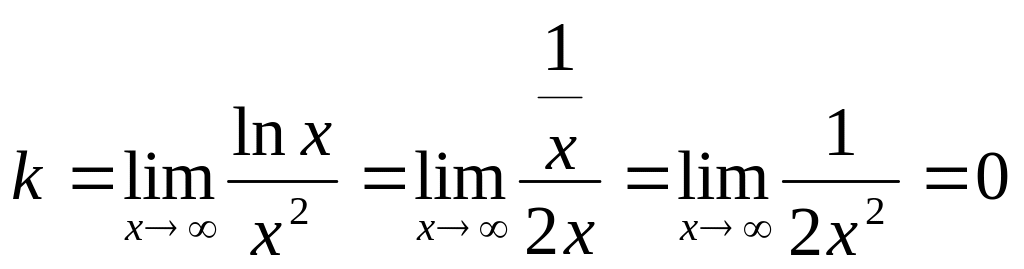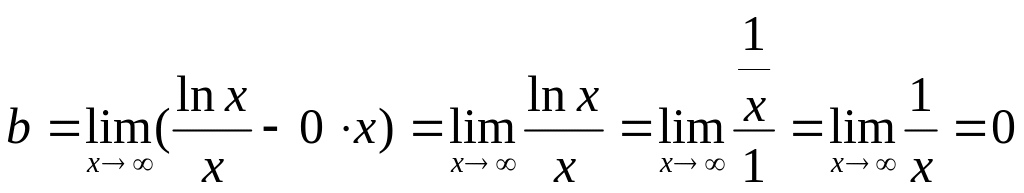(При нахождении пределов воспользовались правилом Лопиталя).
Итак,
и уравнение асимптоты
.
Таким образом, график имеет в качестве
асимптот оси координат.
Найдем производную функции и критические точки:
.
Стационарная критическая точка:
.
Исследуем знак производной на
интервалах(0;е) и (е;).
х
0
е
+
-
Составим таблицу:
x
(0;e)
e
(e;+)
y`
+
0
-
y
возрастает
max
убывает
Экстремум функции:
.
Найдем вторую производную и значения х, при которых график может иметь точку перегиба:
,
при
.
Определим знак второй производной в
интервалах
+
-
и
:
-
х
0
+
Составим таблицу:
x
(0;
)
4,48
(
;)
y``
-
0
+
график
выпуклый
точка перегиба
вогнутый
y(
)=3/(
)
0.33
Г
рафик
пересекает ось абсцисс в точке (1;0). Точек
пересечения с осью ординат нет. Строим
эскиз графика функции:
y
x
1
е
е
ПРИМЕР 11. Построить график функции, заданной уравнением в полярных координатах
Решение.
Построим
график данной функции в декартовых
координатах для
:
r
/2
3/2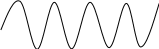
2
φ
0
Из этого графика видно, что
при
имеем
.
Поэтому требуемый график будет находиться
в секторах, соответствующих данным
значениям , а также
в секторах, симметричных им относительно
начала координат (в силу того, что перед
стоит чётный коэффициент).
Учитывая характер изменения r в этих промежутках (от 0 до 1 и затем снова до 0) получим следующий график (восьмилепестковую розу):
ПРИМЕР 12. Исследовать сходимость ряда
Решение.
Проверим, выполняется ли необходимое условие сходимости знакоположительного ряда. Найдём предел общего члена ряда
.
Так как данный предел не равен нулю, то не выполняется необходимое условие сходимости ряда, следовательно, он расходится.
ПРИМЕР 13. Разложить функцию
в ряд по степеням х.
Решение.
Разложим функцию в ряд Маклорена.
Учитывая, что
,
разложим функцию на сумму двух более
простых:
.
Далее преобразуем:
.
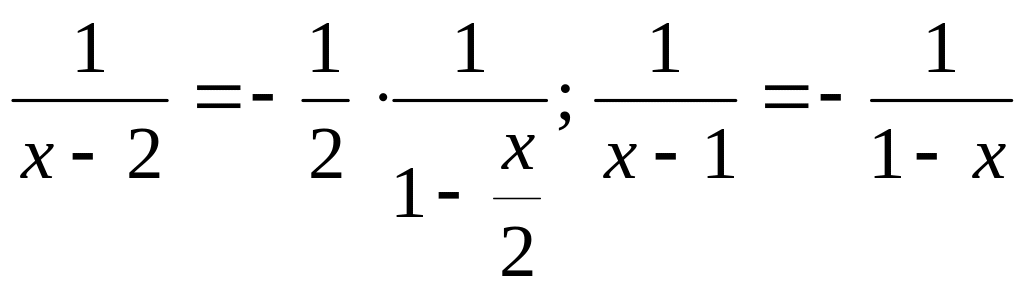Воспользуемся разложением:
.
*
(при
<1, т.е. при
<2)
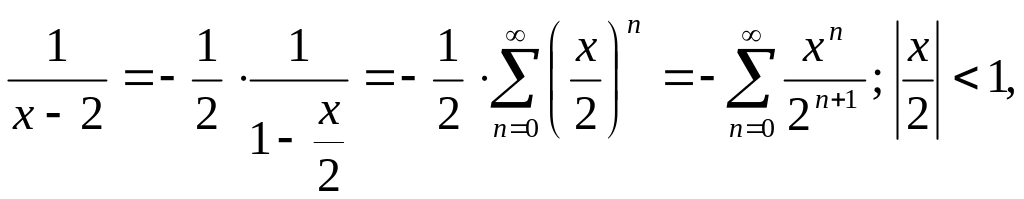то есть
.
Аналогично получим второе разложение:
.
Тогда:
.
Окончательно получаем:
ПРИМЕР 14. Найти неопределённый интеграл
.
Решение.
Введем
подстановку
,
откуда
.
Тогда
.
Находим полученный табличный интеграл
и возвращаемся к прежней переменной:
.
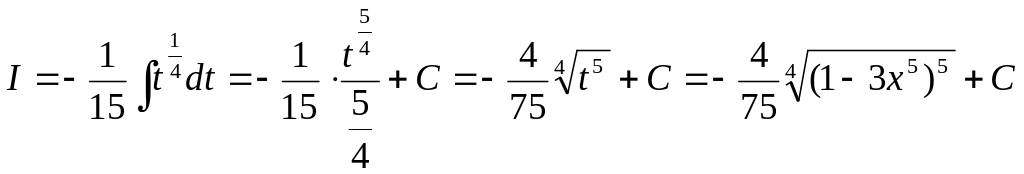ПРИМЕР 15. Найти неопределённый интеграл
.
Решение.
Подведем под знак дифференциала знаменатель подынтегральной дроби:
.
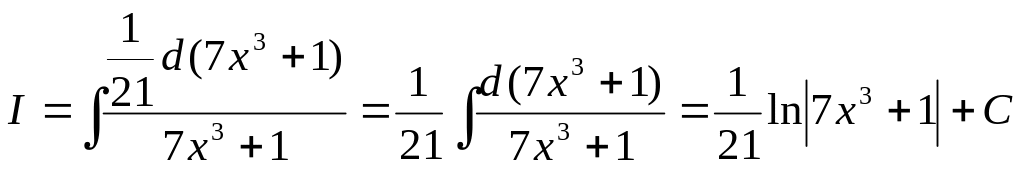ПРИМЕР 16. Найти неопределённый интеграл
.
Решение.
Применим формулу интегрирования по частям: . В данном случае:
.
Подставляя эти выражения в формулу,
получим:
.
ПРИМЕР
17. Вычислить интеграл
или установить его расходимость.
Решение.
Точка
является особой точкой, поскольку
подынтегральная функция имеет в ней
бесконечный разрыв. Поэтому:
- получили бесконечный предел.
Таким образом, данный интеграл расходится.
ПРИМЕР
18. Решить уравнение:
.
Решение.
Данное уравнение является дифференциальным уравнением первой степени с Разделяющимися переменными. Разделим переменные:
.
Проинтегрируем части последнего равенства:
.
Отсюда:
.
Окончательно имеем:
- общее решение данного уравнения.
ПРИМЕР
19. Решить уравнение:
.
Решение.
Данное дифференциальное уравнение относится к типу однородных дифференциальных уравнений
,
которые решаются с помощью подстановки
.
Отсюда:
.
После подстановки в исходное уравнение получим:
.
Это – уравнение с разделяющимися переменными. Разделяем переменные:
Интегрируя обе части, получим:
Используя обратную подстановку, получим:
Окончательно имеем обще решение в виде:
.
Теперь, чтобы найти частное решение, подставляем в общее решение начальное условие:
.
Искомое частное решение:
.