2.32. Уравнения некоторых типов кривых в параметрической форме о кружность

Если центр окружности находится в начале координат, то координаты любой ее точки могут быть найдены по формулам:

0  t  360⁰

Если исключить параметр t, то получим каноническое уравнение окружности:

x² + y² = r²(cos²t + sin²t) = r²

Эллипс

К аноническое уравнение: .

В

C M(x, y)

t

О N P

Для произвольной точки эллипса М(х, у) из геометрических соображений можно записать: из ОВР и из OCN, где а- большая полуось эллипса, а b- меньшая полуось эллипса, х и у – координаты точки М.

Тогда получаем параметрические уравнения эллипса:

где 0  t  2

Угол t называется эксцентрическим углом.

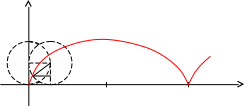
Циклоида

у

С

М К

О Р В а 2а х

Определение. Циклоидой называется кривая, которую описывает некоторая точка, лежащая на окружности, когда окружность без скольжения катится по прямой.

Пусть окружность радиуса а перемещается без скольжения вдоль оси х. Тогда из геометрических соображений можно записать: OB = = at; PB = MK = asint;

MCB = t; Тогда y = MP = KB = CB – CK = a – acost = a(1 – cost).

x = at – asint = a(t – sint).

Итого: при 0  t  2 - это параметрическое уравнение циклоиды.

Если исключить параметр, то получаем:

Как видно, параметрическое уравнение циклоиды намного удобнее в использовании, чем уравнение, непосредственно выражающее одну координату через другую.

Астроида

Данная кривая представляет собой траекторию точки окружности радиуса R/4, вращающейся без скольжения по внутренней стороне окружности радиуса R.

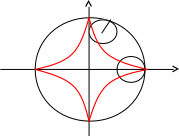
R/4

R

Параметрические уравнения, задающие изображенную выше кривую,

, 0  t  2,

Преобразуя, получим: x^2/3 + y^2/3 = a^2/3(cos²t + sin²t) = a^2/3

2.33. Производная функции, заданной параметрически

Пусть

Предположим, что эти функции имеют производные и функция x = (t) имеет обратную функцию t = Ф(х).

Тогда функция у = (t) может быть рассмотрена как сложная функция y = [Ф(х)].

т.к. Ф(х) – обратная функция, то

Окончательно получаем:

Таким образом, можно находить производную функции, не находя непосредственной зависимости у от х.

Пример. Найти производную функции

Способ 1: Выразим одну переменную через другую , тогда

Способ 2: Применим параметрическое задание данной кривой: .

x² = a²cos²t;

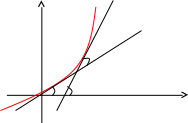
2.34. Кривизна плоской кривой

 

В

А А В

Определение: Угол  поворота касательной к кривой при переходе от точки А к точке В называется углом смежности.

Соответственно, более изогнута та кривая, у которой при одинаковой длине больше угол смежности.

Определение: Средней кривизной К_ср дуги называется отношение соответствующего угла смежности  к длине дуги .

Отметим, что для одной кривой средняя кривизна ее различных частей может быть различной, т.е. данная величина характеризует не кривую целиком, а некоторый ее участок.

Определение: Кривизной дуги в точке К_А называется предел средней кривизны при стремлении длины дуги  0.

Легко видеть, что если обозначить = S, то при условии, что угол  - функция, которая зависит от S и дифференцируема, то

Определение: Радиусом кривизны кривой называется величина .

Пусть кривая задана уравнением y = f(x).

y

B



A  +

x

K_cp = ; ;

Если  = (x) и S = S(x), то .

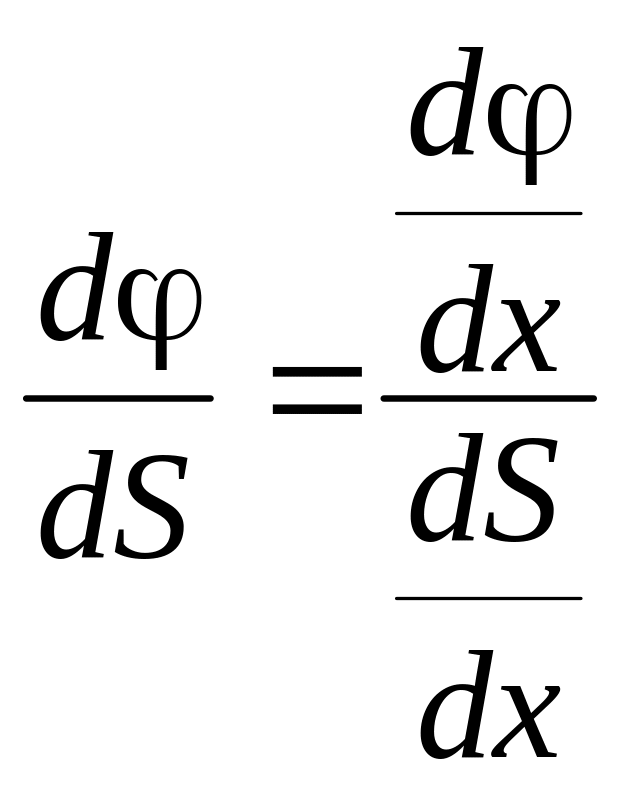В то же время .

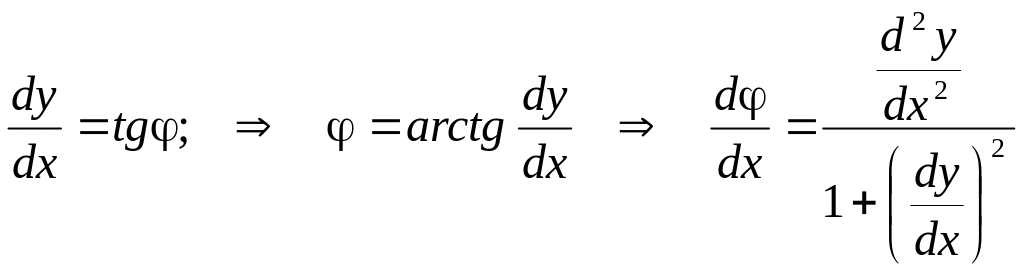Для дифференциала дуги: , тогда

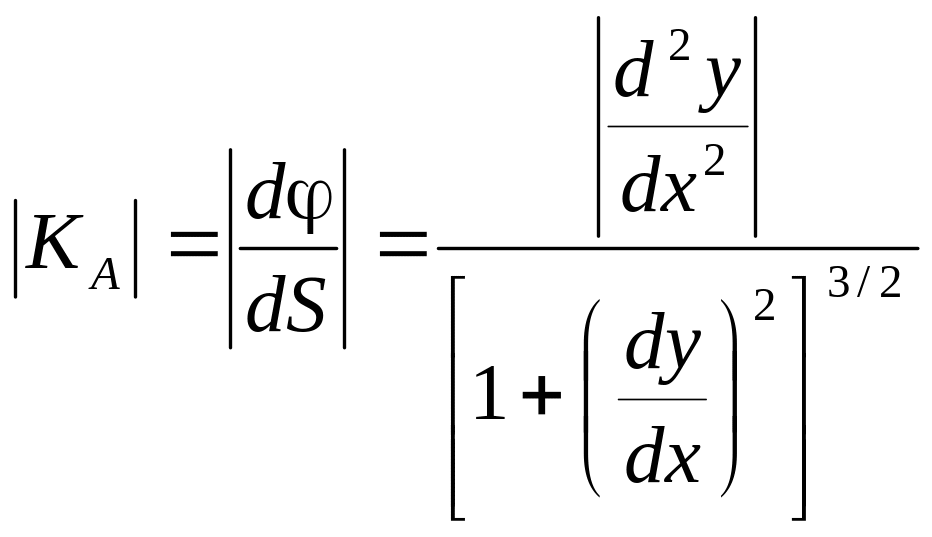Т.к. . В других обозначениях: .

Рассмотрим кривую, заданную уравнением: y = f(x).

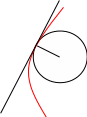
A

C(a, b)

Если построить в точке А кривой нормаль, направленную в сторону выпуклости, то можно отложить отрезок АС = R, где R – радиус кривизны кривой в точке А. Тогда точка С(a, b) называется центром кривизны кривой в точке А.

Круг радиуса R с центром в точке С называется кругом кривизны.

Очевидно, что в точке А кривизна кривой и кривизна окружности равны.

Можно показать, что координаты центра кривизны могут быть найдены по формулам:

Определение: Совокупность всех центров кривизны кривой линии образуют новую линию, которая называется эволютой по отношению к данной кривой. По отношению к эволюте исходная кривая называется эвольвентой.

Приведенные выше уравнения, определяющие координаты центров кривизны кривой определяют уравнение эволюты.