
- •Содержание
- •1. Теоретическая часть
- •1.1. Открытие углеродных нанотрубок и распространённость нанотрубок в природных и технологических средах
- •1.2. Основные типы и структура углеродных нанотрубок
- •1.3. Основные способы получения углеродных нанотрубок
- •1.4. Свойства и применение углеродных нанотрубок
- •1.4.1. Механические свойства
- •1.4.2. Баллистический транспорт в наноразмерных системах
- •1.4.3. Полупроводниковые нанотрубки
- •1.4.5. Использование асм для работы с нанотрубками
- •1.4.7. Топливные элементы на основе углеродных нанотрубок
- •1.5. Методы расчетов электронной структуры
- •1.6. Зонная структура углеродных нанотрубок
- •1.6.1. Метод сильной связи
- •1.6.2. Расчеты зонной структуры углеродных нанотрубок методом сильной связи
- •1.6.3. Другие методы расчета углеродных нанотрубок
- •1.6.4. Экспериментальные данные по зонной структуре нанотрубок
- •1.7. Метод функционала плотности
- •1.7.1. Принцип минимума функционала энергии в терминах волновых функций уравнения Шредингера
- •1.7.2. Плотность электронных состояний
- •1.7.3. Теоремы Хоэнберга – Кона
- •1.7.4. Самосогласованные уравнения Кона – Шэма и обменно-корреляционная энергия
- •1.7.5. Приближение lda
- •2. Практическая часть
- •2.1. Программное обеспечение, используемое в работе
- •2.1.1. Программный комплекс Gaussian
- •2.1.2. Базисные наборы в Gaussian
- •2.1.3. Программное обеспечение TubeGen
- •2.1.4. Файлы заданий в Gaussian
- •2.1.5. Этапы расчета
- •2.2. Задания
- •2.3. Задания для самостоятельной работы
- •2.4. Вопросы
- •2.4. Рекомендуемая форма отчётности
- •3. Рекомендуемая литература
1.7. Метод функционала плотности
1.7.1. Принцип минимума функционала энергии в терминах волновых функций уравнения Шредингера
Стационарное уравнение Шредингера имеет вид
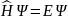 (3)
(3)
где
E – энергия электронов, Ψ
= Ψ(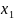 ,
,
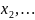
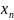 )
– волновая функция системы, а Ĥ –
оператор Гамильтона:
)
– волновая функция системы, а Ĥ –
оператор Гамильтона:
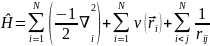 (4)
(4)
где
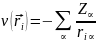 – внешний потенциал (в данном случае
учитывается только влияние ядер с
зарядом α на электрон i). Координаты
– внешний потенциал (в данном случае
учитывается только влияние ядер с
зарядом α на электрон i). Координаты
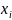 включают в себя как пространственные
включают в себя как пространственные
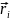 ,
так и спиновые координаты
,
так и спиновые координаты
 .
Можно записать (4) в виде
.
Можно записать (4) в виде
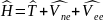 ,
где
,
где
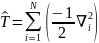 – оператор кинетической энергии,
– оператор кинетической энергии,
 – оператор взаимодействия электронов
с ядрами, а
– оператор взаимодействия электронов
с ядрами, а
 – оператор отталкивания электронов.
Общая энергия W записывается в виде W
= E
+ Vnn,
где
– оператор отталкивания электронов.
Общая энергия W записывается в виде W
= E
+ Vnn,
где
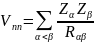 – энергия межъядерного отталкивания.
При этом не имеет значения включать ли
Vnn
в
– энергия межъядерного отталкивания.
При этом не имеет значения включать ли
Vnn
в
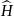 и решать уравнение Шредингера вида
и решать уравнение Шредингера вида
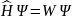 ,
или решать уравнение ĤΨ = EΨ
и добавить Vnn
к полученной энергии.
,
или решать уравнение ĤΨ = EΨ
и добавить Vnn
к полученной энергии.
Решения
уравнения (3) должны соответствовать
определенным граничным условиям. В
частности Ψ не должна иметь разрывов и
убывать к нулю на больших расстояниях
от атома или молекулы или иметь
периодическое поведение для бесконечного
кристалла.
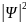 представляет собой распределение
вероятности в том смысле, что
представляет собой распределение
вероятности в том смысле, что
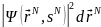 – вероятность обнаружить систему в
состоянии с пространственными координатами
между
– вероятность обнаружить систему в
состоянии с пространственными координатами
между
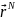 и
и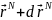 и спиновыми координатами
и спиновыми координатами
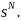 Здесь
Здесь
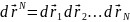 ,
обозначает набор
,
обозначает набор
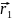 ,
,
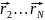 ,
а
,
а
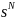 обозначает набор
обозначает набор
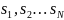 .
.
Существует
множество независимых решений (3) Ψk
с соответствующими им собственными
значениями Ek.
Набор Ψk
является полным и Ψk
могут быть сделаны ортонормированными:
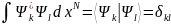 .
.
В
дальнейшем, волновая функция основного
состояния будет обозначаться
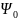 ,
а энергия E0.
Ожидаемые значения кинетической и
потенциальной энергий даются как
,
а энергия E0.
Ожидаемые значения кинетической и
потенциальной энергий даются как
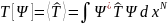 и
и
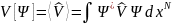 соответственно. Другими словами они
являются функционалами
Ψ
соответственно. Другими словами они
являются функционалами
Ψ
Предположим,
что система находится в состоянии Ψ,
которое, возможно, не удовлетворяет
уравнению (3). Тогда среднее значение
энергии этой системы по множеству
измерений дается формулой
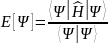 .
.
Поскольку
измерения дают одно из собственных
значений
мы получаем
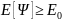 .
Энергия, вычисленная из предполагаемой
Ψ, является верхней границей для энергии
основного состояния
.
Энергия, вычисленная из предполагаемой
Ψ, является верхней границей для энергии
основного состояния
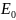 .
Полная минимизация функционала E[Ψ]
по всем разрешенным волновым функциям
даст волновую функцию основного состояния
Ψ0
и энергию E[Ψ0]
= E0,
то есть
.
Полная минимизация функционала E[Ψ]
по всем разрешенным волновым функциям
даст волновую функцию основного состояния
Ψ0
и энергию E[Ψ0]
= E0,
то есть
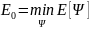 .
.
1.7.2. Плотность электронных состояний
В
системе электронов, число электронов
на единицу объёма в данном состоянии
называется электронной плотностью для
данного состояния. Обозначим его ρ(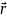 ).
В терминах волновых функций ρ(
)
выражается формулой
).
В терминах волновых функций ρ(
)
выражается формулой
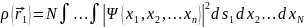 .
.
Это
неотрицательная простая функция трех
переменных x, y
и z, интеграл от которой дает полное
число электронов:
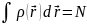 .
.
Для
атома в основном состоянии электронная
плотность монотонно убывает при удалении
от ядра схоже с экспоненциальной
зависимостью. Для молекул, на первый
взгляд, может показаться, что электронные
плотности являются суперпозицией
атомных плотностей. Однако, при более
глубоком рассмотрении (экспериментальном
и теоретическом) существенные (но
достаточно малые по величине) “уплотнения”
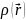 наблюдаются в областях химических
связей.
наблюдаются в областях химических
связей.
Для
любого ядра в атоме, молекуле или
кристалле электронная плотность имеет
конечное значение (для атома обозначим
его
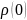 ).
Другой важный результат – закон убывания
электронной плотности на больших
расстояниях:
).
Другой важный результат – закон убывания
электронной плотности на больших
расстояниях:
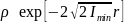 ,
где Imin
– точное значение первого ионизационного
потенциала.
,
где Imin
– точное значение первого ионизационного
потенциала.
