3.1 Вопросы для самопроверки

1. Что называется вектором?

2. Как найти проекции вектора, если известны координаты его начала и конца?

3. Что такое модуль вектора и как его найти?

4. Чему равно скалярное произведение векторов, заданных проекциями?

5. Как найти угол между векторами?

6. Чему равна площадь треугольника?

7. Чему равен объем пирамиды?

8. Напишите канонические уравнения прямой.

9. Как найти прямую, проходящую через две точки?

10. Как найти уравнение плоскости, проходящей через три точки?

11. Сформулируйте условие перпендикулярности прямой и плоскости.

4 Кривые второго порядка

Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат

(1)

Коэффициенты уравнения – действительные числа, но по крайней мере одно из чисел А, В или С отлично от нуля. Такие линии называются линиями (кривыми) второго порядка.

Общее уравнение второго порядка (1) определяет на плоскости (если не считать случаев вырождения и распадения) следующие кривые: окружность, эллипс, гиперболу, параболу.

Теорема 1.

Для любой линии второго порядка существует прямоугольная система координат, в которой уравнение этой линии имеет один из следующих видов:

1) , эллипс;

2) , мнимый эллипс;

3) , пара мнимых пересекающихся прямых;

4) гипербола;

5) пара пересекающихся прямых;

6) , парабола;

7) , пара параллельных прямых;

8) , пара мнимых параллельных прямых;

9) , пара совпадающих прямых;

10) , окружность.

Уравнения 1) – 10) называются каноническими уравнениями линий второго порядка.

Рассмотрим частные случаи уравнения (1) при В=0.

1. Окружность

Окружностью радиуса R с центром в точке называется множество всех точек плоскости, равноудаленных от точки на расстояние R .

Каноническое уравнение окружности имеет вид:

. (2)

Уравнение окружности с центром в начале координат имеет вид:

(3)

Рис.2. Окружность

с центром в начале координат

Рис.1. Окружность

с центром в точке

Пример 1.1.

Найти координаты центра и радиус окружности .

Решение.

Выделим полные квадраты:

;

; .

Центр окружности находится в точке (2; -4), радиус равен 7.

Пример 1.2.

Составить уравнение окружности, диаметром которой является отрезок, отсекаемый координатными осями от прямой .

Решение.

Преобразуем общее уравнение прямой:

; ; .

Получили уравнение прямой в отрезках. Эта прямая пересекает координатные оси в точках А(-12; 0) и B(0; 8).

.

Рис.3

Центром окружности является точка - середина отрезка АВ. Координаты этой точки найдем по формулам координат середины отрезка:

; .

Значит, .

Радиус найдем как расстояние между точками и B:

.

Запишем уравнение окружности:

.

Преобразовав это уравнение, мы получим общее уравнение окружности:

; .

Ответ: .

Задачи для самостоятельного решения:

Составить уравнение окружности в каждом из следующих случаев:

1. Центр окружности совпадает с началом координат и ее радиус .

2. Центр окружности совпадает с точкой и ее радиус .

3. Окружность проходит через точку и ее центр совпадает с точкой .

4. Точки и являются концами одного из диаметров окружности.

5. Центр окружности совпадает с началом координат и прямая является касательной к окружности.

6. Центр окружности совпадает с точкой и прямая является касательной к окружности.

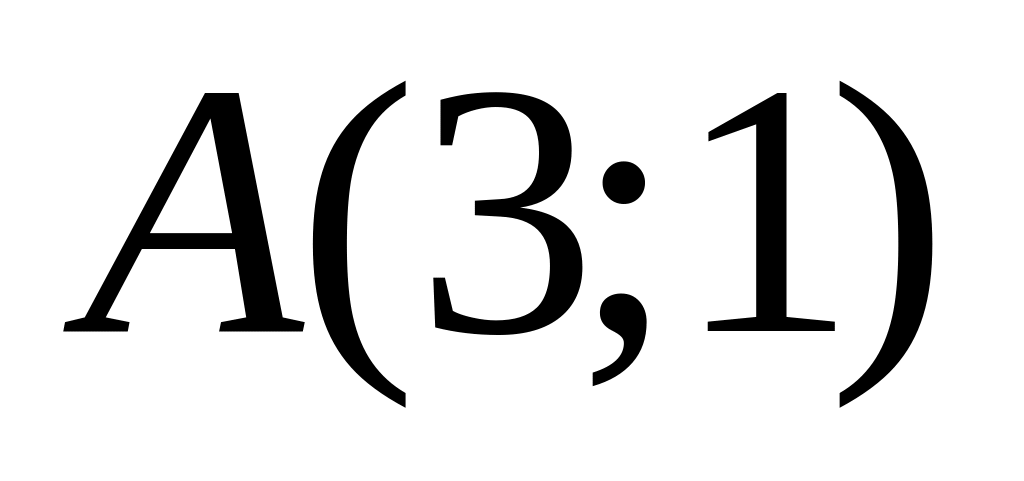7. Окружность проходит через точки и , а ее центр лежит на прямой .

8. Окружность проходит через три точки , , .

9. Окружность касается прямых , , причем одной из них – в точке .

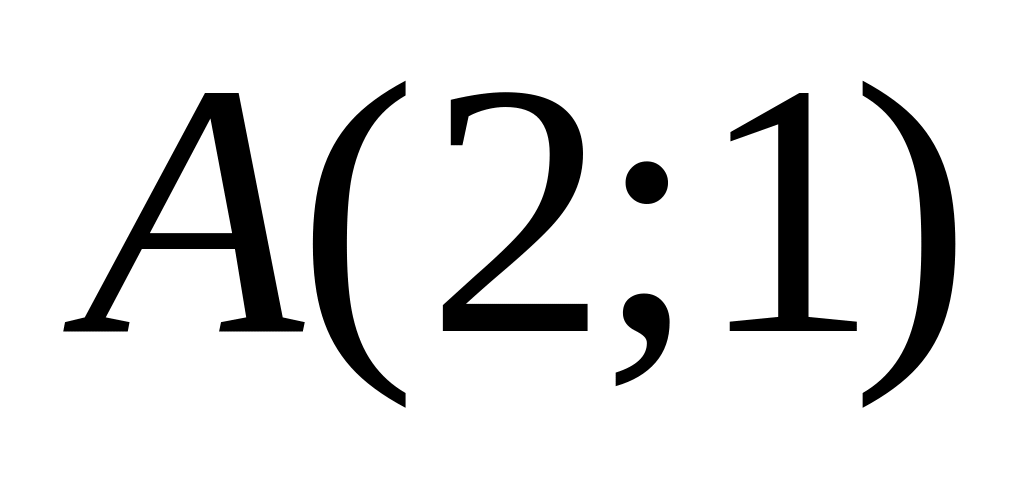10. Окружность касается прямых , , центр лежит на прямой .

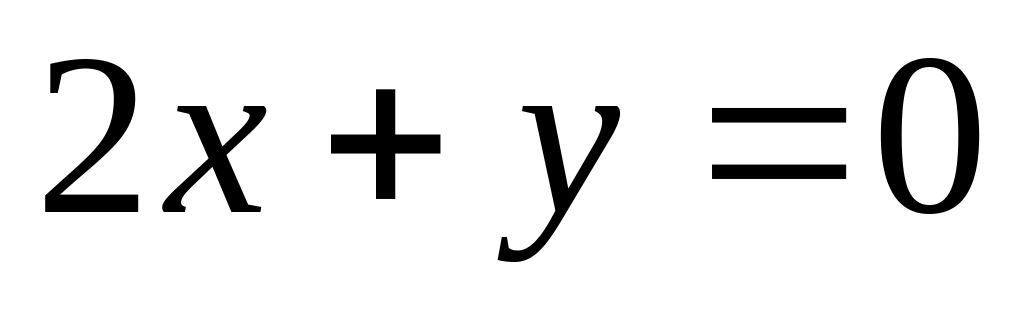1. Эллипс

Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой же плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Каноническое уравнение эллипса имеет вид:

, (4)

где - большая полуось, - малая полуось эллипса, - фокусное расстояние.

Из определения следует, что .

Числа , , связаны соотношением

. (5)

Отсюда следует, что .

Координаты фокусов , . Фокусы эллипса лежат на оси .

Точки A, B, C, D называются вершинами эллипса, точка O – центром эллипса.

Из уравнения (4) следует, что каждое слагаемое в левой части не превосходит единицы, т.е. имеют место неравенства и или и . Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми , .

Если , то уравнение (4) определяет окружность , рассматриваемую как частный случай эллипса.

Важными характеристиками эллипса являются:

- эксцентриситет показывает степень вытянутости, обозначается буквой («эпсилон»):

(0< <1). (6)

- директрисы эллипса – прямые с уравнениями

, . (7)

- фокальные радиусы – расстояния и от произвольной точки эллипса до его фокусов ( до левого, до правого) определяются формулами:

, . (8)

Если фокусы эллипса лежат на оси , то , большая ось лежит на оси , малая ось - на оси , , , уравнения директрис . Координаты фокусов , .

Рис.4. Эллипс и его директрисы

Пример 2.1.

Дан эллипс . Найти: 1) его полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис.

Решение.

1) Разделим все члены уравнения на 225:

.

Получили каноническое уравнение эллипса. Из уравнения (4): , .

Тогда большая полуось равна , малая полуось . На самом деле, . Большая ось лежит на оси , малая ось лежит на оси .

2) По формуле (5): , значит фокусное расстояние . Фокусы эллипса находятся в точках и . Неравенство выполняется.

3) По формуле (6) вычислим эксцентриситет эллипса . Видим, что, действительно, 0< <1.

4) В нашем случае директрисы находятся по формулам (7): ; ; . Это прямые, параллельные оси и проходящие через точки .

Пример 2.2.

Составить уравнение эллипса, симметричного относительно координатных осей, проходящего через точку и имеющего эксцентриситет .

Решение.

Из формул (4)-(6) составим систему уравнений относительно параметров а, b:

Из второго уравнения находим:

, т.е. , т.е. .

Подставляя это в первое уравнение, получим , , тогда , , .

Уравнение эллипса .

Пример 2.3.

Составить уравнение эллипса, симметричного относительно координатных осей и проходящего через точки и . Найти эксцентриситет эллипса, расстояния от точки до фокусов и уравнения его директрис.

Решение.

Параметры a и b найдем, подставив в уравнение (4) координаты точек A и B. Это приводит к системе

Отсюда, с учетом , находим: , .

Каноническое уравнение эллипса найдено: .

Фокусное расстояние .

Эксцентриситет равен .

Расстояния от точки до фокусов:

; .

Уравнения директрис:

левая директриса: правая директриса: .

Задачи для самостоятельного решения:

1. Дан эллипс . Найти: 1) его полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис.

2. Дан эллипс . Найти: 1) его полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис.

3. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, зная, кроме того, что:

1) его полуоси равны 5 и 2;

2) его большая ось равна 10, а расстояние между фокусами ;

3) его малая ось равна 24, а расстояние между фокусами ;

4) расстояние между его фокусами и эксцентриситет ;

5) его большая ось равна 20, а эксцентриситет ;

6) его малая ось равна 10, а эксцентриситет ;

7) расстояние между директрисами равно 5 и расстояние между фокусами ;

8) его большая ось равна 8, а расстояние между директрисами равно 16;

9) его малая ось равна 6, а расстояние между директрисами равно 13;

10) расстояние между директрисами равно 32 и ;

11) точка эллипса и его малая полуось ;

12) точка эллипса и его большая полуось ;

13) точки и эллипса;

14) точка эллипса и расстояние между его фокусами ;

15) точка эллипса и его эксцентриситет ;

16) точка эллипса и его эксцентриситет ;

17) точка эллипса и расстояние от нее до левого фокуса;

18) точка эллипса и расстояние между его директрисами, равное 10.

4. Составить уравнение эллипса, фокусы которого лежат на оси ординат симметрично относительно начала координат, зная, кроме того, что:

1) его полуоси равны соответственно 7 и 2;

2) его большая ось равна 10, а расстояние между фокусами ;

3) расстояние между его фокусами и эксцентриситет ;

4) его малая ось равна 16, а эксцентриситет ;

5) расстояние между директрисами равно и расстояние между фокусами ;

6) расстояние между директрисами равно и .

5. На эллипсе найти точки, абсцисса которых равна .

6. Определить, какие из точек , , , , , , , , , лежат на эллипсе , какие внутри и какие вне его.

7. Вычислить площадь четырехугольника, две вершины которого лежат в фокусах эллипса , а две другие совпадают с концами его малой оси.

8. Вычислить площадь четырехугольника, две вершины которого лежат в фокусах эллипса , а две другие совпадают с концами его малой оси.

9. Эксцентриситет эллипса , фокальный радиус точки эллипса равен 10. Вычислить расстояние от точки до односторонней с этим фокусом директрисы.

10. Эксцентриситет эллипса , расстояние от точки эллипса до директрисы равно 20. Вычислить расстояние от точки до фокуса, одностороннего с этой директрисой.

11. Эксцентриситет эллипса , центр его совпадает с началом координат, один из фокусов . Вычислить расстояние от точки эллипса с абсциссой, равной 2, до директрисы, односторонней с данным фокусом.

12. Эксцентриситет эллипса , центр его совпадает с началом координат, одна из директрис дана уравнением . Вычислить расстояние от точки эллипса с абсциссой, равной , до фокуса, одностороннего с данной директрисой.

13. Дана точка на эллипсе ; составить уравнения прямых, на которых лежат фокальные радиусы точки .

14. Убедившись, что точка лежит на эллипсе , определить фокальные радиусы точки .

15. Определить точки эллипса , расстояние которых до правого фокуса равно 14.

16. Определить точки эллипса , расстояние которых до левого фокуса равно 2,5.

17. На прямой найти точку, одинаково удаленную от левого фокуса и верхней вершины эллипса .

18. Составить уравнение геометрического места точек, расстояния которых от точки в два раза меньше расстояния до прямой .