
- •1 Первообразная функции и неопределенный интеграл
- •1.1 Таблица интегралов
- •2 Методы подстановки и замены переменного
- •2.1 Вопросы для самопроверки
- •2.2 Примеры для самостоятельного решения
- •3 Интегрирование по частям
- •3.1 Вопросы для самопроверки
- •3.2 Примеры для самостоятельного решения
- •4 Интегрирование выражений, содержащих квадратный трехчлен
- •4.1 Вопросы для самопроверки
- •4.2 Примеры для самостоятельного решения
- •5 Интегрирование рациональных дробей
- •5.1 Вопросы для самопроверки
- •5.2 Примеры для самостоятельного решения
- •6 Интегрирование тригонометрических функций Рассмотрим интегралы вида
- •6.1 Вопросы для самопроверки
- •6.2 Примеры для самостоятельного решения
- •7 Варианты индивидуальных заданий
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
|
Кафедра математики
ЕН. Ф. 01 МАТЕМАТИКА
Методические указания к проведению практических занятий по теме
«Неопределенный интеграл. Часть 1»
для студентов всех специальностей
Уфа 2010
УДК 51(07)
ББК 22.1я73,22.161.6
М 54
Рекомендовано к изданию методической комиссией факультета механизации сельского хозяйства (протокол № 3 от 31.03.2010 года).
Составители: доцент Лукманов Р.Л.
доцент Каптелинина Ф.И.
Рецензент: доцент кафедры физики Юмагужин Р.Ю.
Ответственный за выпуск: зав. кафедрой математики
доцент Лукманов Р.Л.
Оглавление
Введение 4
1 Первообразная функции и неопределенный интеграл 4
-
Таблица интегралов 4
2 Методы подстановки и замены переменного 5
2.1 Вопросы для самопроверки 7
2.2 Примеры для самостоятельного решения 7
3 Интегрирование по частям 7
3.1 Вопросы для самопроверки 10
3.2 Примеры для самостоятельного решения 10
4 Интегрирование выражений, содержащих квадратный трехчлен 10
4.1 Вопросы для самопроверки 12
4.2 Примеры для самостоятельного решения 12
5 Интегрирование рациональных дробей 12
5.1 Вопросы для самопроверки 17
5.2 Примеры для самостоятельного решения 17
6 Интегрирование тригонометрических функций 17
6.1 Вопросы для самопроверки 21
6.2 Примеры для самостоятельного решения 21
7 Варианты индивидуальных заданий 21
Введение
Целью настоящих методических указаний является помощь студентам в изучении трудно усваиваемого раздела «Неопределенный интеграл», имеющего большое применение как в самой математике, так и в различных областях науки и техники.
Методические указания содержат: краткие теоретические сведения, решение типовых примеров, вопросы для самопроверки, варианты расчетно-графических заданий и список рекомендуемой литературы. При работе с данными методическими указаниями студентам рекомендуется изучить соответствующий теоретический материал по учебникам [1] – [3]. Большое количество решенных примеров представлено в руководстве к решению задач [7].
1 Первообразная функции и неопределенный интеграл
Функция
![]() называется первообразной функции
называется первообразной функции
![]() ,
если
,
если
![]() .
.
Другими
словами, задача нахождения первообразной
равносильна восстановлению функции
![]() по ее производной
по ее производной
![]() .
.
Например,
для функции
![]() ,
первообразная
,
первообразная
![]()
Как видим, первообразная определяется не единственным образом, а с точностью до постоянного слагаемого.
Вообще говоря, не любая функция имеет первообразную. Можно доказать, что любая непрерывная функция имеет первообразную, то есть непрерывность является достаточным условием существования первообразной для заданной функции.
Множество
всех первообразных функции функций
![]() называется неопределенным интегралом
и обозначается
называется неопределенным интегралом
и обозначается
![]() .
.
Отметим, что операции дифференцирования и интегрирования взаимнообратны в следующем смысле:
1)
![]() ,
,
2)
![]() .
.
1.1 Таблица интегралов
-
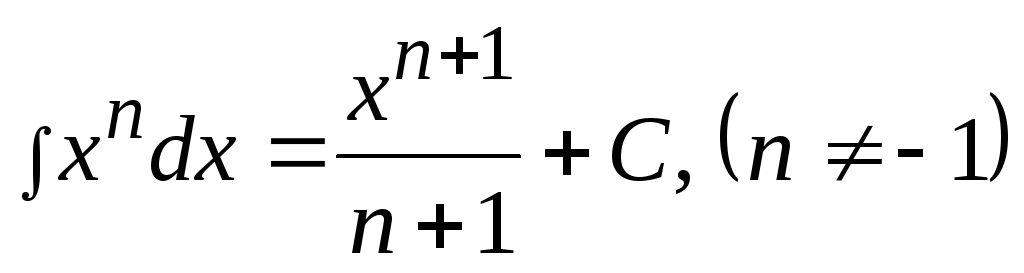 7)
7) ,
, -
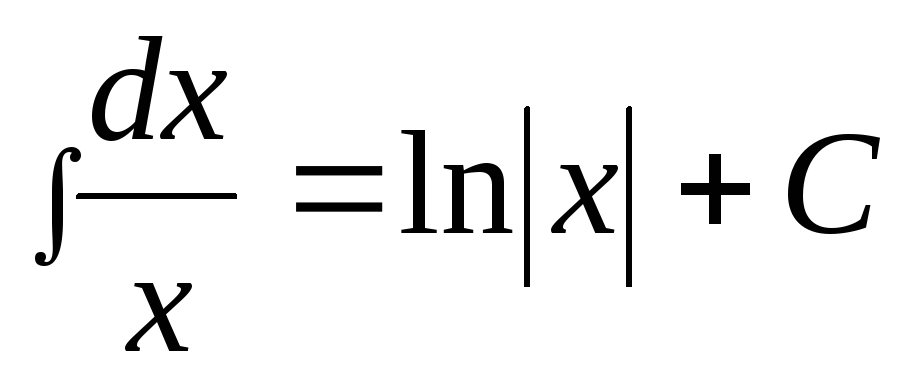 ,
8)
,
8)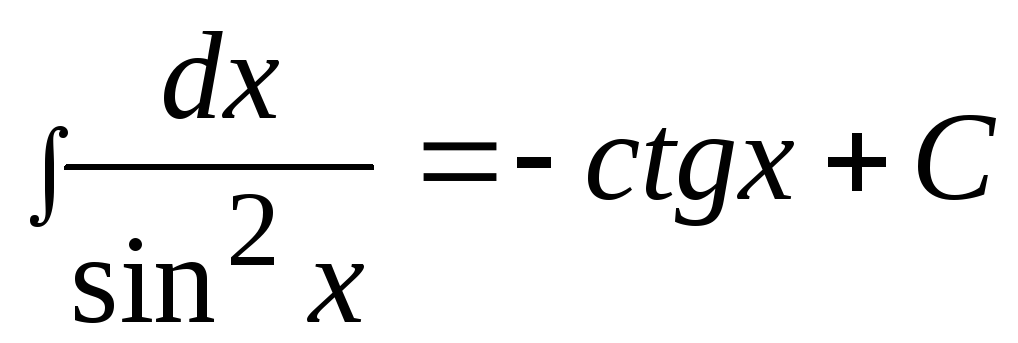 ,
, -
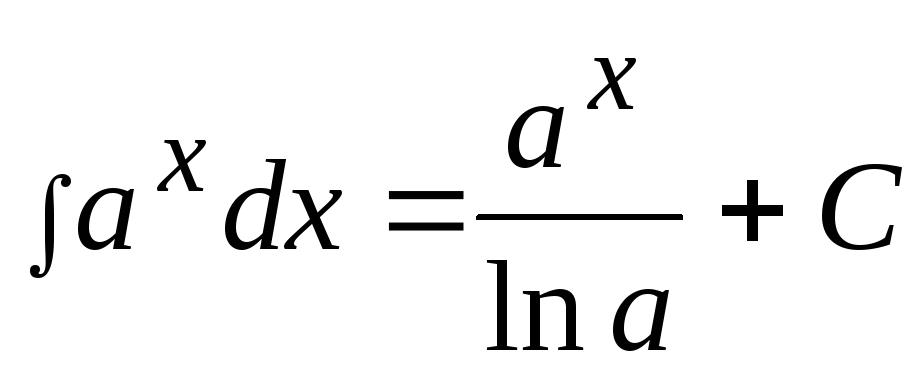 ,
9)
,
9) ,
, -
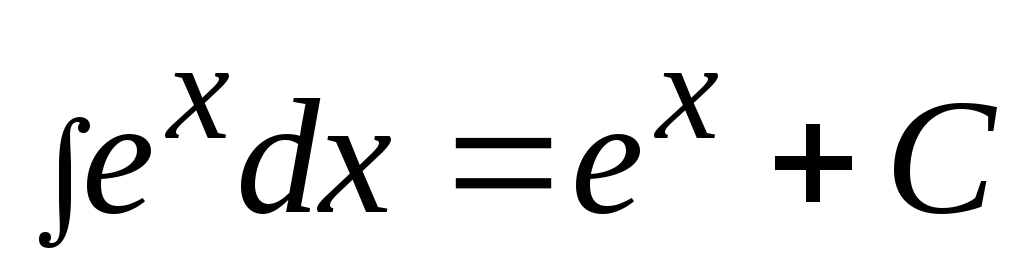 ,
10)
,
10) ,
, -
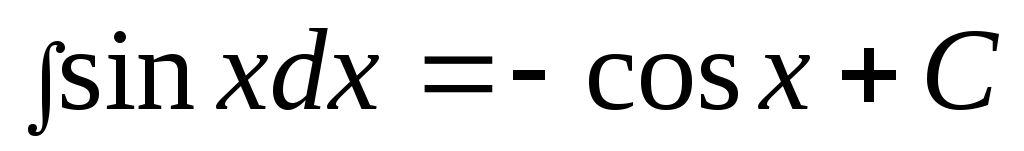 , 11)
, 11)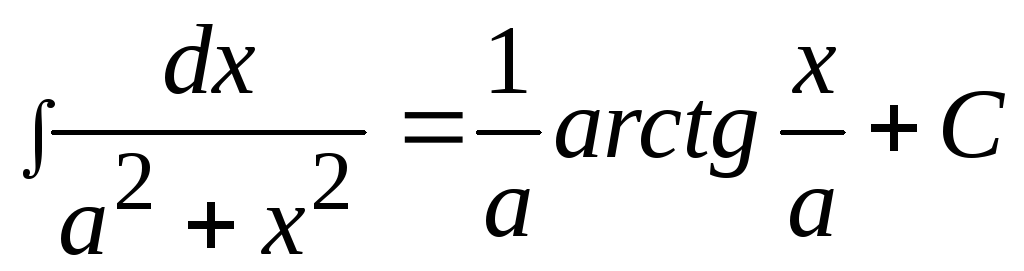 ,
,
-
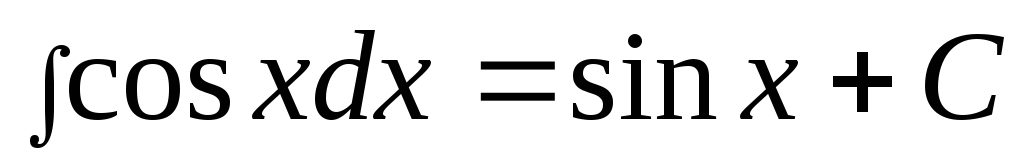 ,
12)
,
12)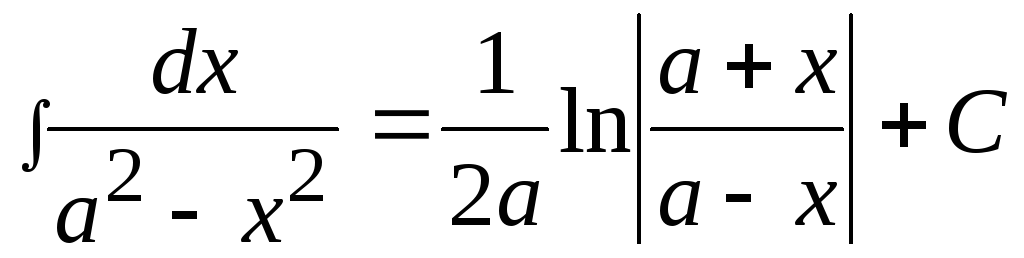 .
.
Нетрудно заметить, что большинство формул таблицы получено из таблицы производных.
Примеры применения формулы 1):
Пример
1.
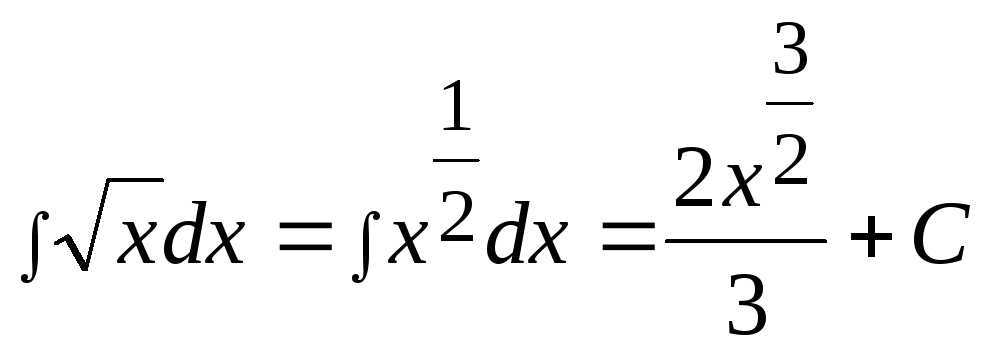 .
.
Пример
2.
![]() .
.
Пример
3.
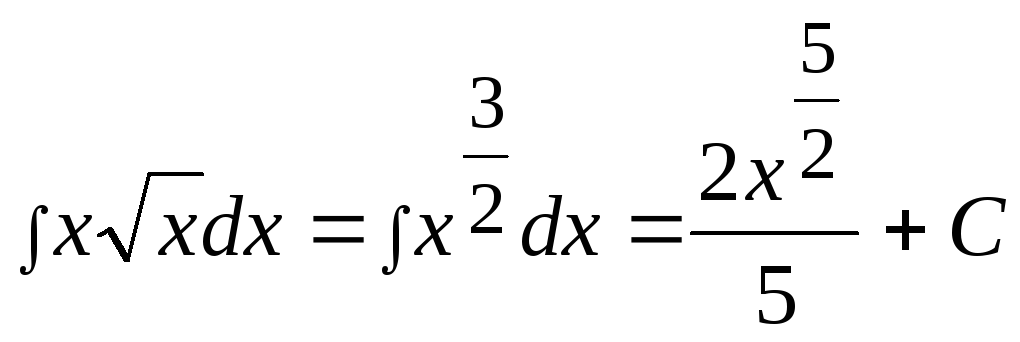 .
.
Пример
4.
![]() .
.
Как мы увидим в дальнейшем, особую роль при вычислении интегралов играют формулы 9) – 12). Рассмотрим примеры их применения:
Пример
5.
![]() .
.
Пример
6.
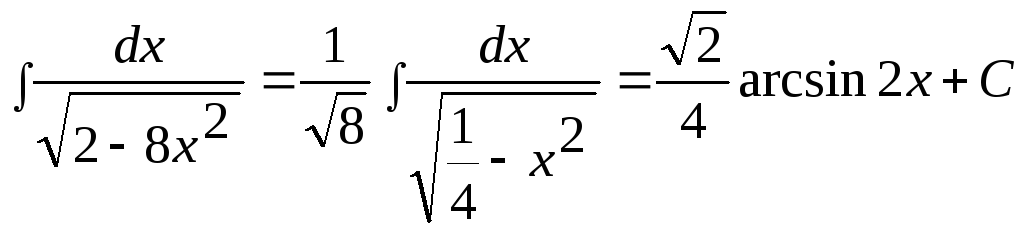 .
.
Пример
7.
![]()
![]() .
.
2 Методы подстановки и замены переменного
Пусть
требуется найти неопределенный интеграл
от непрерывной функции
![]() .
.
Рассмотрим
некоторую функцию
![]() ,
которая имеет непрерывную производную
,
которая имеет непрерывную производную
![]() и обратную функцию
и обратную функцию
![]() .
(Например:
.
(Например:
![]() монотонна). Тогда справедлива формула:
монотонна). Тогда справедлива формула:
![]() .
(2.1)
.
(2.1)
В
некоторых ситуациях удается подобрать
функцию
![]() так, что интеграл в правой части (1)
оказывается проще, чем в левой части.
Такой прием называется методом замены
переменной. На практике часто формулу
используют в обратную сторону:
так, что интеграл в правой части (1)
оказывается проще, чем в левой части.
Такой прием называется методом замены
переменной. На практике часто формулу
используют в обратную сторону:
![]() (2.1)
(2.1)
Другими
словами, если подынтегральное выражение
может быть записано в форме левой части
(2.1), то с помощью подстановки
![]() получаем более простой интеграл.
получаем более простой интеграл.
Пример
8.
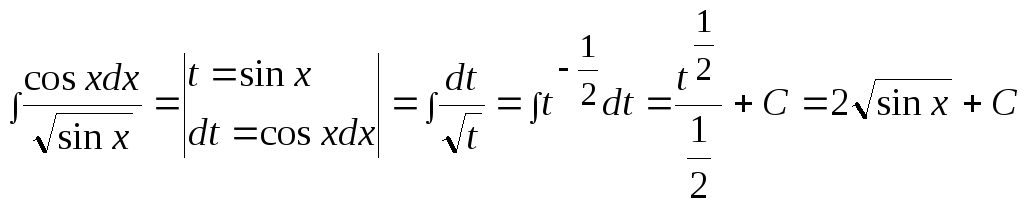 .
.
Пример
9.
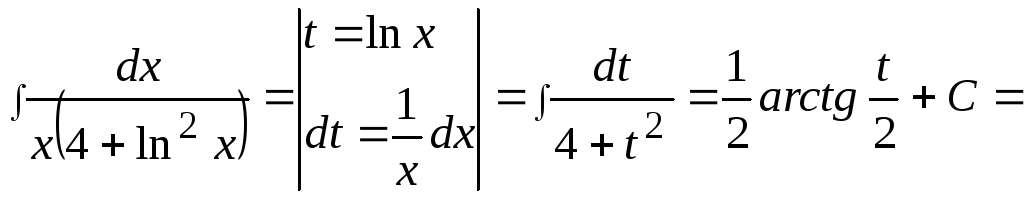
![]() .
.
Правильность вычисления интеграла можно проверить: производная найденного интеграла должна совпадать с подынтегральной функцией. В нашем примере:
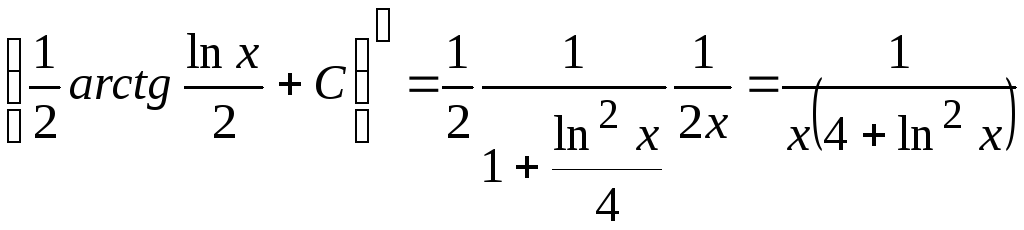 .
.
Пример
10.
 .
.
Пример
11.
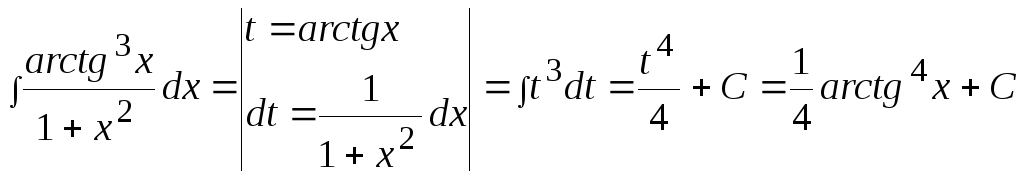 .
.
На практике часто используется следующая простая формула:
![]() , (2.2)
, (2.2)
где
![]() - первообразная функции
- первообразная функции
![]() .
.
Пример
12.
![]() .
.
Пример
13.
![]() .
.
Пример
14.
![]() .
.
2.1 Вопросы для самопроверки
-
Что называется первообразной функции
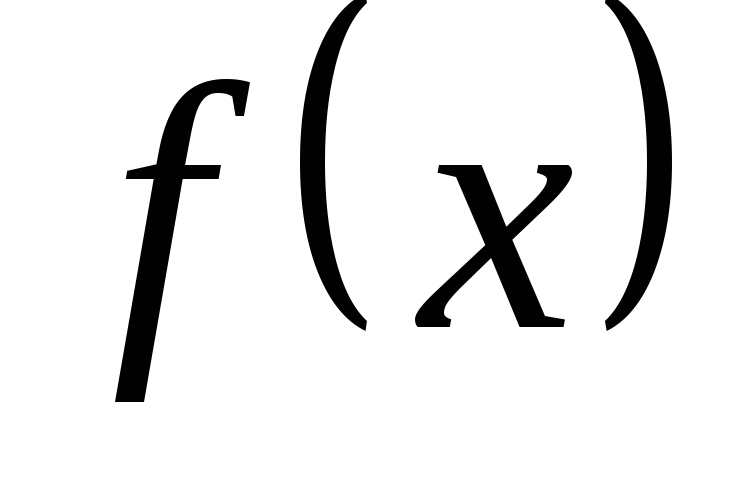 ?
? -
Что означает произвольная постоянная интегрирования «С»?
-
В чем заключается основная идея метода замены переменной?
-
Каким условиям должна удовлетворять функция
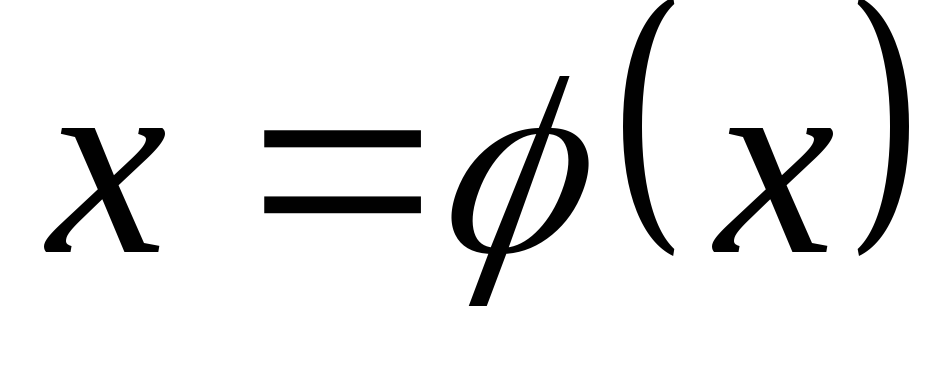 при замене переменной?
при замене переменной?
2.2 Примеры для самостоятельного решения
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
3 Интегрирование по частям
![]() (3.2)
(3.2)
Она получается почленным интегрированием формулы производной произведения. Иногда используют другую форму записи формулы (2.1)
![]() (3.
(3.![]() )
)
Смысл формулы в том, что производная перебрасывается с одного сомножителя на другой и интеграл при этом может оказаться проще, чем исходный.
Можно выделить по крайней мере два класса интегралов, для которых применима формула интегрирования по частям.
-
 ,
,
где
![]() - многочлен степени n.
В качестве
- многочлен степени n.
В качестве
![]() нужно взять
нужно взять
![]() ,
а
,
а
![]() - другой сомножитель.
- другой сомножитель.
При этом формулу приходится применить столько раз, какова степень многочлена
II.
 .
.
В
этом случае, наоборот, следует положить
![]() =
=![]() .
.
Рассмотрим применение указанной схемы.
Пример
15. ![]() .
.
Это интеграл первого типа, поэтому:
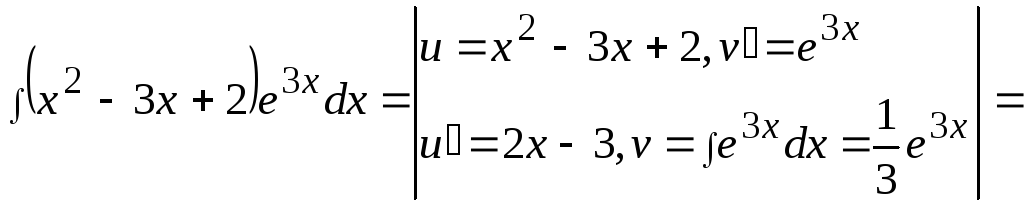
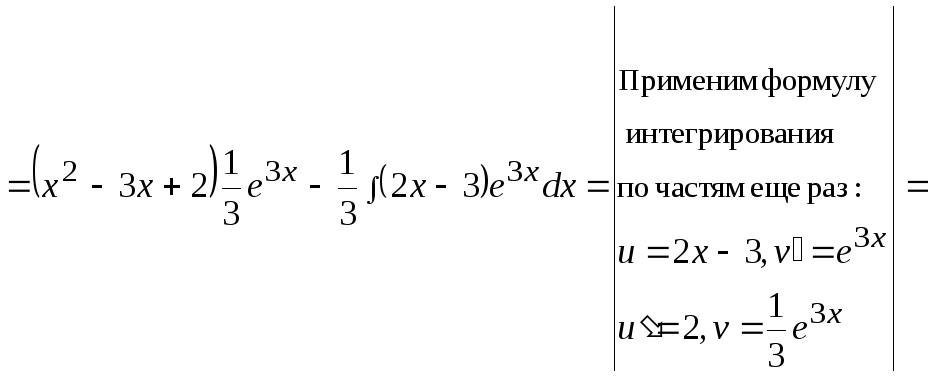
![]()
![]() .
.
Пример
16.
![]() .
.
Это интеграл второго типа, поэтому имеем:
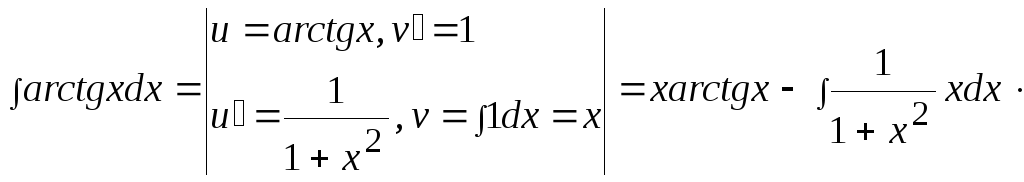
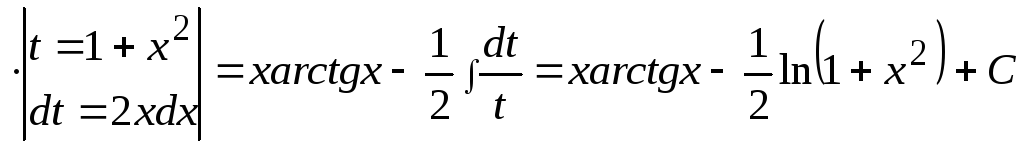
Заметим,
что при использовании формулы
интегрирования по частям приходится
восстанавливать функцию
![]() по
ее производной
по
ее производной
![]() .
Поэтому в качестве сомножителя
.
Поэтому в качестве сомножителя
![]() нужно брать легко интегрируемую функцию.
нужно брать легко интегрируемую функцию.
Формула интегрирования по частям может хорошо сработать и в других случаях.
Пример17.
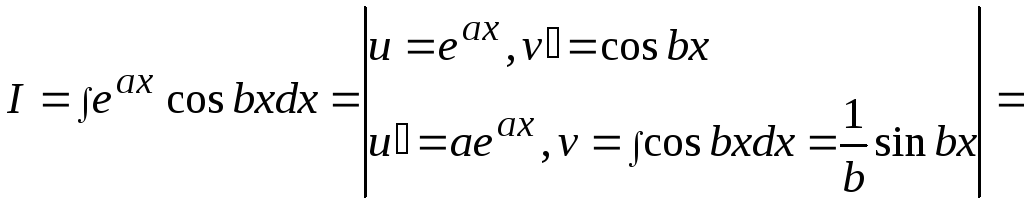
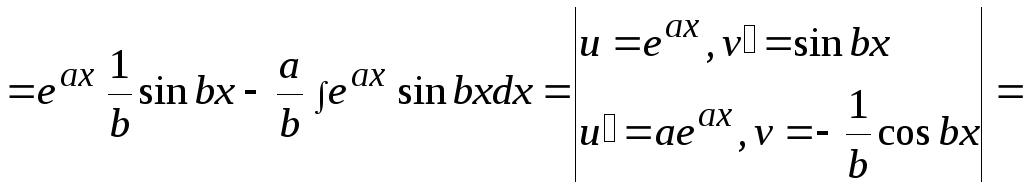
![]()
![]() .
.
Получили уравнение относительного исходного интеграла I. Вынося I за скобку, получим
![]() ,
,
откуда
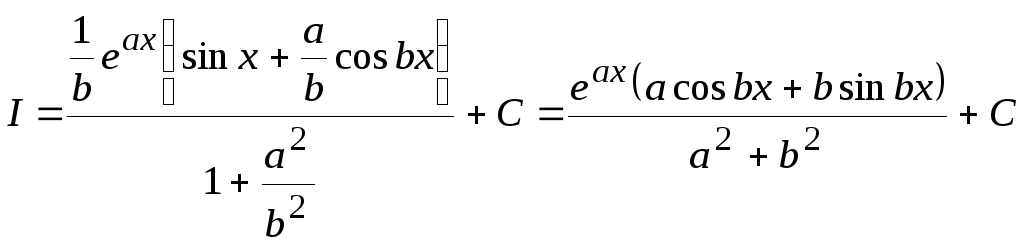 .
.
Пример
18.
![]() .
.
В
этом примере целесообразно прежде
сделать замену переменной. Введем
обозначения
![]() ,
тогда
,
тогда
![]() ,
,
![]() .
.
После подстановки получим интеграл:
![]()
Это интеграл предыдущего вида. Рекомендуем самостоятельно довести до конца решение этого примера.
Пример
19.
![]() .
.
Нетрудно
заметить, что
![]() и
и
![]() берется по формуле
берется по формуле
![]() ,
поэтому введем следующие обозначения:
,
поэтому введем следующие обозначения:
![]()
![]()
Используя формулу интегрирования по частям, получим:
![]()
![]() .
.
В
следующем примере выбор u
и
![]() определяется тем, что u
предстоит дифференцировать (что возможно
при любой сложности ее задания), а
определяется тем, что u
предстоит дифференцировать (что возможно
при любой сложности ее задания), а
![]() - интегрировать (что возможно далеко не
всегда).
- интегрировать (что возможно далеко не
всегда).
Пример
20.
![]() .
.
Введем
обозначения
![]() ,
или
,
или
![]()
![]() .
.
По формуле интегрирования по частям имеем:

Найдем полученный интеграл следующим образом:
![]()
![]() .
.
Окончательно получим:
![]() .
.
Таким образом, получили линейное уравнение относительно искомого интеграла, решая которое, получим:
![]() .
.
![]() .
.

