БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ
Кафедра математики
Ен. Ф. 01 математика
Методические указания
Строительство
Уфа 2005
1 Решение систем линейных уравнений методами Крамера, Гаусса и обратной матрицы
Пусть дана система n уравнений с n неизвестными:
Основная матрица А такой системы квадратная. Определитель этой матрицы
называется определителем системы.
Если определитель системы отличен от нуля, то система называется невырожденной и имеет единственное решение.
В дальнейшем мы будем иметь дело только с такими системами.
Наиболее простым методом для решения таких систем линейных уравнений является метод Крамера.
Формулы
Крамера имеют вид:
(1.1.1)
Более универсальным и эффективным является метод Гаусса, состоящий в последовательном исключении неизвестных.
Решение
осуществляется в два этапа: 1) система
приводится к треугольному виду, 2)
последовательно определяют неизвестные
.
Предварительно приведем вопросы по разделу, на которые следует ответить перед решением задач и на зачете.
1. Основные понятия, связанные с матрицами (матрица-строка, матрица-столбец, определитель квадратной матрицы и т.п.)
2. Сложение матриц и умножение матрицы на число. Свойства этих действий.
3. Умножение матриц и его свойства.
4. Обратная матрица, ее строение.
5. Матричная запись системы линейных алгебраических уравнений, решение ее с помощью обратной матрицы.
6. Решение матричных уравнений с помощью обратной матрицы.
7. Исследование системы уравнений первой степени общего вида; основная и расширенная матрицы; ранг матрицы; теорема Кронекера-Капелли.
Пример 1.
Решить систему уравнений методами Крамера, Гаусса и обратной матрицы:
Решение:
а) Метод Крамера.
Найдем
определитель системы
.
Предварительно сложив второй столбец
с третьим и разложив определитель по
элементам последнего столбца.
=
=2(-1)
=-2(-2-3)=10
.
Так
как
,
то система имеет единственное решение.
Найдем
определители
и
,
заменив в матрице коэффициентов
соответственно первый, второй, третий
столбцы столбцом свободных членов (при
вычислении определителя
преобразования аналогичные предыдущему.)
=
=2(-1)
-2(-1-4)=10.
При
вычислении определителя
последнюю
строку складываем с первой и вычитаем
из второй строки. Разлагаем по элементам
последнего столбца.
=
=1(-1)
=10+10=20.
При
вычислении определителя
последнюю
строку складываем с первой и со второй
строкой, и разлагаем получившийся
определитель по элементам второго
столбца.
=
=-1(-1)
=50-20=30.
Подставляя найденные значения в формулы (1.1.1), получим:
х=
у=
z=
б) Метод Гаусса.
Составим расширенную матрицу системы:
Разрешающим
элементом
удобно иметь единицу, поэтому переставим
второе уравнение на место первого.
Получим нули в первом столбце, умножив первое уравнение последовательно на (-2) и (-3) и складывая со вторым и третьим.
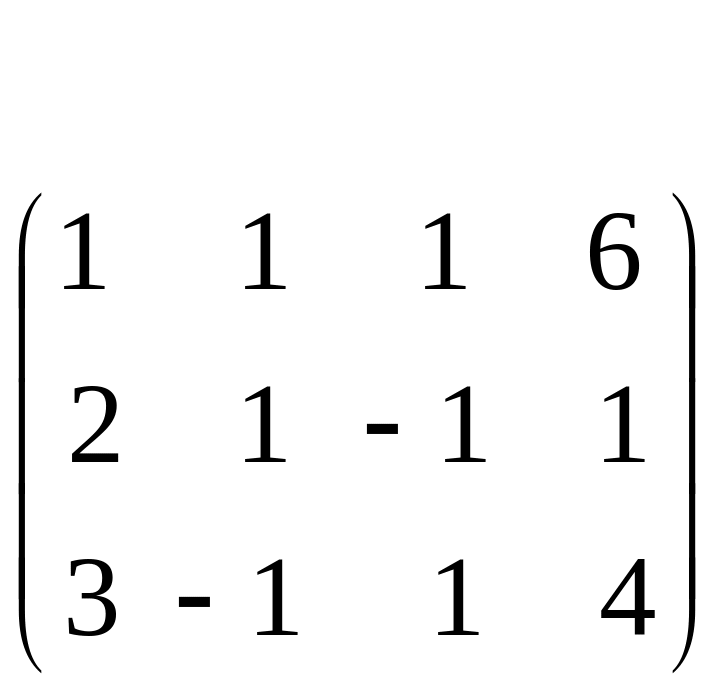
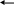
(-2)
(-3)
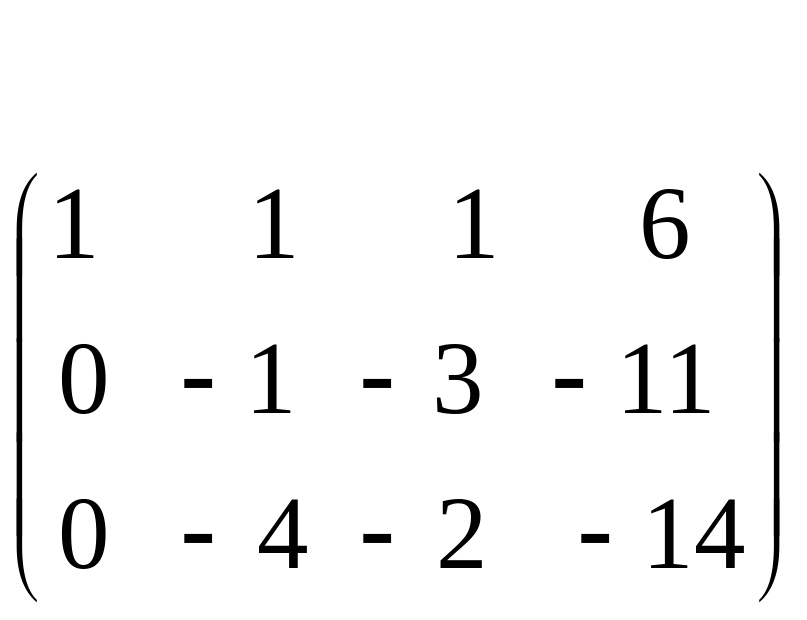
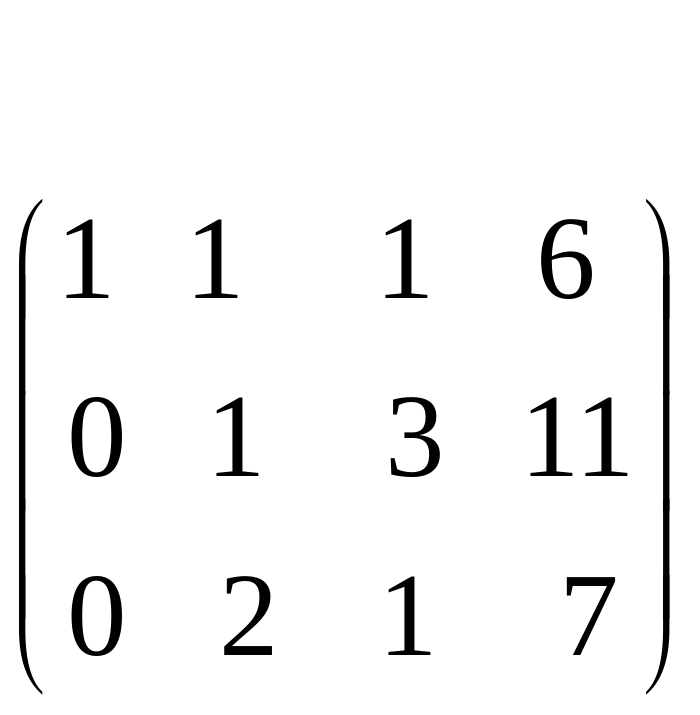
С помощью второго элемента второй строки сделаем нуль во втором столбце третьей строки, для чего умножим вторую строку на (-2) и сложим с третьей.
(-2)
.
Таким образом, свели матрицу к треугольному виду. Запишем полученную систему уравнений:
Из последнего уравнения сразу находим значение z=3, подставляя которое во второе уравнение находим у=11-3z=11-9=2. Затем из первого уравнения найдем
х=1, у=2, z=3.
в) Метод обратной матрицы.
Задача. Данную систему уравнений записать в матричной форме и решить ее c помощью обратной матрицы:
x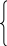
1—
2х2
+ x3=1,
2x1+3х2 — x3=8,
x1 — х2 + 2х3=-1.
Решение. Обозначим через А матрицу коэффициентов при неизвестных; Х — матрицу-столбец неизвестных x1, x2, x3; H - матрицу-столбец свободных членов:
1
-2 1 x1
1
А= 2 3 -1 , Х= x2 , Н= 8 .
1 -1 2 x3 -1
С учетом этих обозначений данная система уравнений принимает следующую матричную форму:
А Х=Н (l)
Если
матрица
А
—
невырожденная
(ее
определитель
отличен от
нуля),
то
она
имеет обратную
матрицу
А-1.
Умножив
обе
части
уравнения
(1) на
А-1,
получим:
Но
(Е
—
единичная
матрица),
а
ЕХ=Х,
Поэтому
(2)
Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матри-цу А-1.
Пусть имеем невырожденную матрицу
а11
а12
а13
А=
а21
а22 а23
. Тогда А-1=
а31
а32
а33
где Аij (i=1, 2, 3; j=l, 2, 3) — алгебраическое дополнение элемента аij в определителе матрицы А, которое является произведением (-l)i+j на минор (определитель) второго порядка, полученный вычеркиванием i-й строки и j-гo столбца в определителе матрицы А.
Вычислим определитель и алгебраические дополнения Аij элементов матрицы А.
1 -2 1
=
2 3 -1 =10
0
– следовательно, матрица А имеет обратную
матрицу А-1
1 -1 2
Тогда
5
3 -1
А-1=
=
-5 1 3
-5
-1 7
По формуле (2) находим решение данной системы уравнений в матричной форме:
=
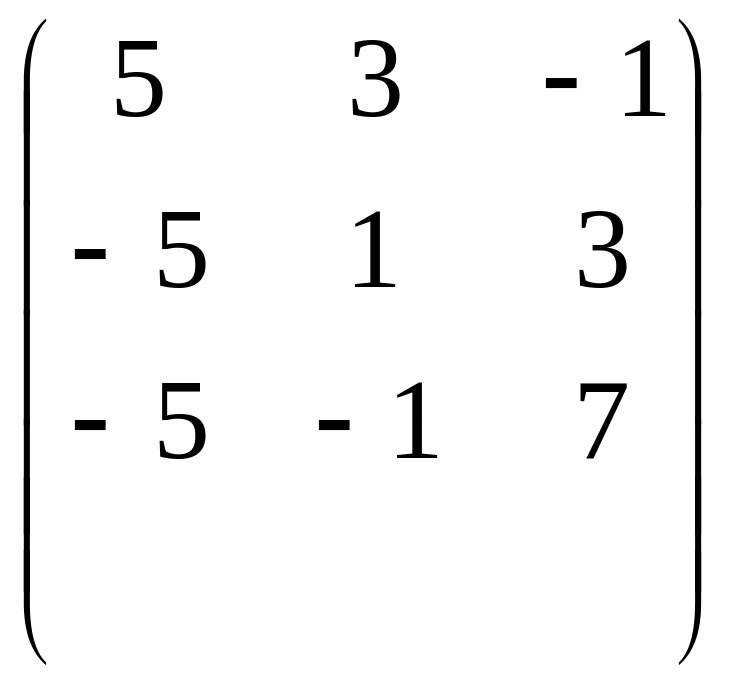
Отсюда, x1=3, x2 =0, x3=-2
Далее рассмотрим образец решения некоторых типовых задач.
Задача 1. Исследовать систему линейных уравнений; если она совместна, то найти ее общее и одно частное решение.
Решение. Приведем расширенную матрицу системы к ступенчатому виду:
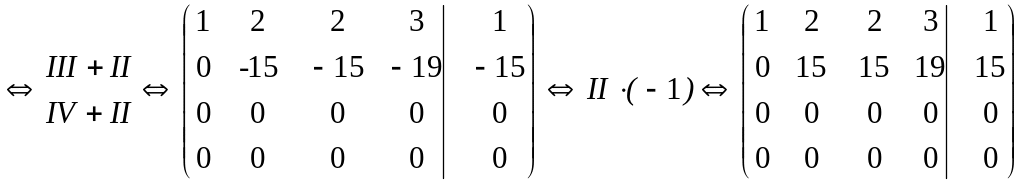
Так
как
,
то система совместна и неопределена.
Количество
главных переменных равно
,
количество свободных переменных равно
.
Выберем
какой-нибудь отличный от нуля минор
второго порядка полученной матрицы
,
например, минор
.
Его столбцы – первый и второй столбцы
матрицы
- соответствуют переменным
и
- это будут главные
переменные, а
и
- свободные переменные.
Заметим,
что в качестве главных переменных в
данном примере нельзя выбрать пару
и
,
т.к. любой соответствующий им минор
равен нулю:
,
,
.
Запишем систему уравнений, соответствующую полученной расширенной матрице:
Перепишем ее в виде:
или
Обозначим
свободные переменные:
через
,
через
.
Запишем общее решение системы:
;
частное решение
.
Задача 2. Исследовать систему линейных уравнений:
Решение. Приведем к ступенчатому виду расширенную матрицу системы:
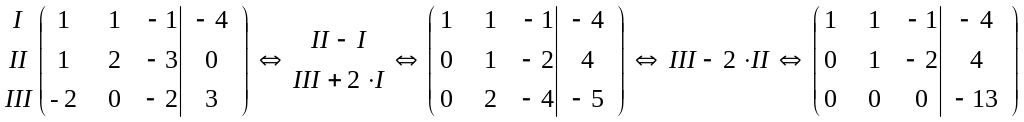
Так
как
,
то система несовместна (не имеет решений).
В самом деле, последней строке полученной
расширенной матрицы соответствует
уравнение
,
не имеющее решений.
Ответ: система несовместна.
Задача 3. Найти общее решение и фундаментальную систему решений однородной системы линейных уравнений:
Решение. Приведем матрицу системы к ступенчатому виду:
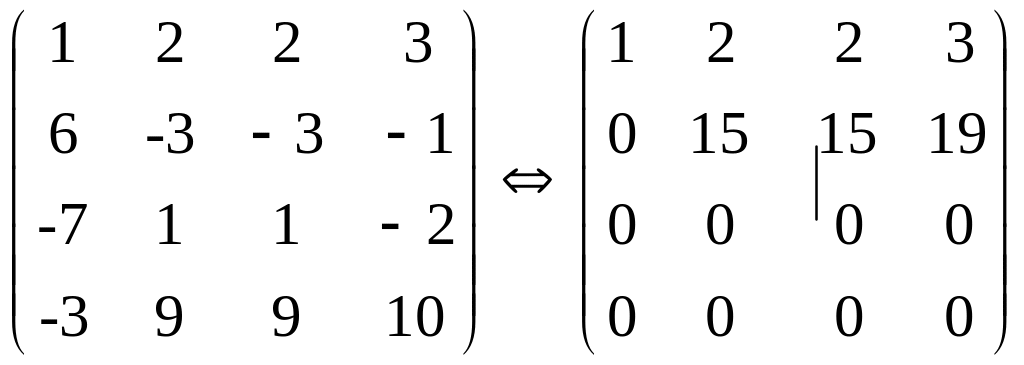
Так как , то система неопределенна. В качестве главных переменных можно выбрать и , соответствующие столбцам ненулевого минора второго порядка: ; в качестве свободных переменных - и .
Запишем систему, соответствующую полученной матрице:
Из
второго уравнения получим
.
Подставляя это
выражение в первое уравнение, получим
.
Обозначая
свободные переменные:
через
,
через
,
запишем общее решение системы:
.
Фундаментальную
систему решений образует, например,
пара решений
и
.
Ответ:
общее решение системы
;
фундаментальная
система решений
.