
- •§ 2. Тройной интеграл
- •1. Определение тройного интеграла
- •2. Вычисление тройного интеграла
- •3. Геометрический смысл тройного интеграла
- •§ 3. Приложения двойных и тройных интегралов
- •5. Вычисление массы тела
- •6. Моменты плоской фигуры
- •7. Координаты центра масс
- •§ 4. Криволинейные координаты и замена переменных в кратных интегралах
- •1. Криволинейные координаты
- •2. Координатные поверхности
- •3. Координатные линии
- •4. Коэффициенты Ламе
- •5. Сферические координаты
3. Геометрический смысл тройного интеграла
В том
случае, если подынтегральная функция
![]() ,
то очевидно, что тройной интеграл
,
то очевидно, что тройной интеграл
![]() даёт нам объём тела
,
по которому ведётся интегрирование.
даёт нам объём тела
,
по которому ведётся интегрирование.
Пример
1. Вычислить объём тела,
ограниченного координатными плоскостями
и плоскостью
![]()
![]() (рис. 11).
(рис. 11).
Решение.
Искомый объём
![]() ,
где тело
есть пирамида, ограниченная плоскостью
,
где тело
есть пирамида, ограниченная плоскостью
![]() и координатными плоскостями.
и координатными плоскостями.
Очевидно, что этот тройной интеграл можно выразить шестью различными способами через трёхкратный:


или

или

Проведём вычисления по последней формуле (нетрудно убедиться, что остальные интегралы вычисляются аналогично), получим
 .
.
Имеем
 .
.
Наконец,
 куб. ед.
куб. ед.
§ 3. Приложения двойных и тройных интегралов
1. Вычисление площади плоской области
Мы установили, что площадь плоской области может быть вычислена по формуле
![]() .
.
2. Вычисление площади кривой поверхности
Ранее мы установили, что площадь кривой поверхности , заданной уравнением и расположенной над областью в плоскости , вычисляется по формуле
![]() ,
,
где
 .
.
3. Вычисление объёма тела
Пусть
тело
ограничено снизу простой областью
,
сверху - поверхностью
![]() непрерывна в области
,
а с боков цилиндрической поверхности,
образующие которой параллельны оси
,
а направляющей служит контур области
,
то объём тела можно вычислить с помощью
двойного интеграла так:
непрерывна в области
,
а с боков цилиндрической поверхности,
образующие которой параллельны оси
,
а направляющей служит контур области
,
то объём тела можно вычислить с помощью
двойного интеграла так:
![]()
или так:
![]() .
.
4. Вычисление массы поверхности
Пусть
в каждой точке поверхности
,
заданной уравнением
плотность равна
![]() ,
где
- непрерывная функция в каждой точке
поверхности
,
а функция
-
непрерывна в области
плоскости
и имеет в ней непрерывные частные
производные
,
где
- непрерывная функция в каждой точке
поверхности
,
а функция
-
непрерывна в области
плоскости
и имеет в ней непрерывные частные
производные
![]() и
и
 .
.
Разбивая
произвольным образом поверхность
на
![]() частей, заметим, что масса
частей, заметим, что масса
![]() -й
ячейки приблизительно равна
-й
ячейки приблизительно равна
![]() ,
где
,
где
![]() - площадь
-й
ячейки, тогда масса всей поверхности
:
- площадь
-й
ячейки, тогда масса всей поверхности
:
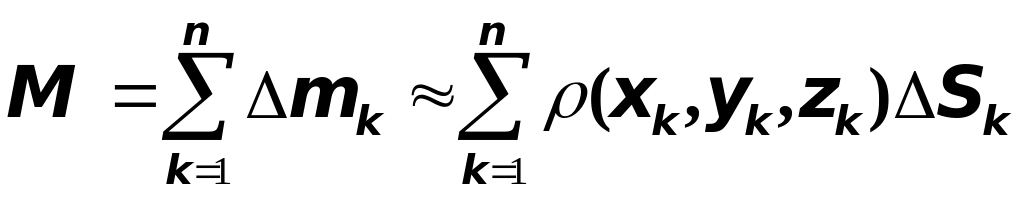 .
.
Справа здесь стоит интегральная сумма для непрерывной функции. Измельчая дробление и устремляя ранг дробления к нулю, в пределе мы получим такую формулу для вычисления массы поверхности :
![]() .
.
В
частности, если поверхность
лежит в плоскости
,
т.е. совпадает с областью
,
то
![]() .
.
5. Вычисление массы тела
Если
в каждой точке тела
,
ограниченного простой поверхностью,
задана плотность
![]() ,
где
,
где
![]() - непрерывная функция в каждой точке
тела
,
то, проведя аналогичные рассуждения,
получим, что масса тела
- непрерывная функция в каждой точке
тела
,
то, проведя аналогичные рассуждения,
получим, что масса тела
![]() .
.
6. Моменты плоской фигуры
Из
курсов теоретической механики известно,
что статическим моментом
![]() материальной точки массы
материальной точки массы
![]() относительно оси
относительно оси
![]() называется произведение массы этой
точки на расстояние до оси
,
т.е.
называется произведение массы этой
точки на расстояние до оси
,
т.е.
![]() .
.
Моментом
инерции
![]() материальной точки относительно оси
называется произведение массы
этой точки на квадрат её расстояния от
оси
,
т.е.
материальной точки относительно оси
называется произведение массы
этой точки на квадрат её расстояния от
оси
,
т.е.
![]() .
.
Статическим моментом системы материальных точек относительно оси называется сумма статических моментов относительно этой оси всех материальных точек, входящих в систему.
Пусть
в плоской области
распределена масса с плотностью
![]() .
Разобьём область
на
частей,
- площадь
-й
ячейки (
.
Разобьём область
на
частей,
- площадь
-й
ячейки (![]() ).
В ячейке
).
В ячейке
![]() возьмём произвольную точку
возьмём произвольную точку
![]() ,
тогда в силу сделанного выше определения
можем считать, что
,
тогда в силу сделанного выше определения
можем считать, что
 .
.
Измельчая
дробление, в пределе получим точные
значения для статических моментов
области
о
осей
![]() и
и
![]() :
:
![]() .
.
Проводя аналогичные рассуждения для моментов инерции области относительно координатных осей, получим
![]() .
.
