С другой стороны

,

откуда следует

.

Рекомендуем сравнить с результатами примера, рассмотренного на стр 48.

Пример 2. Рассмотрим интеграл .

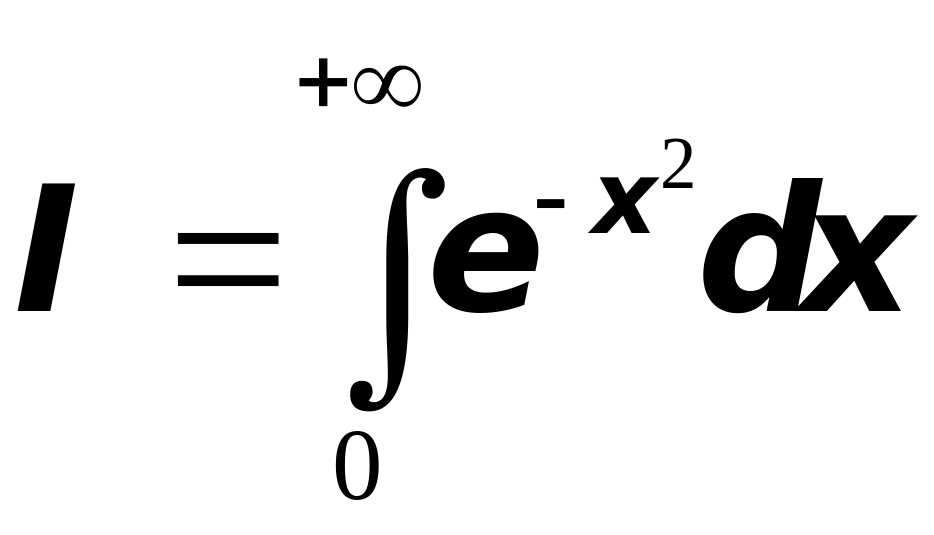Сделаем замену переменной: 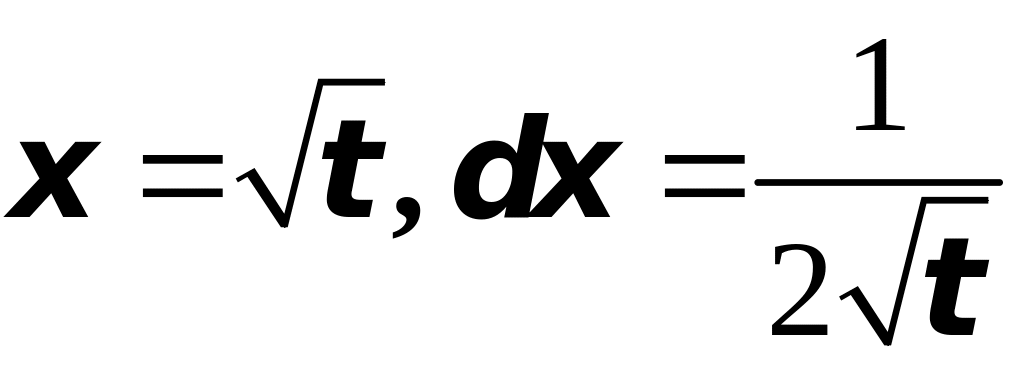. Тогда наш интеграл так выражается через гамма-функцию:

.

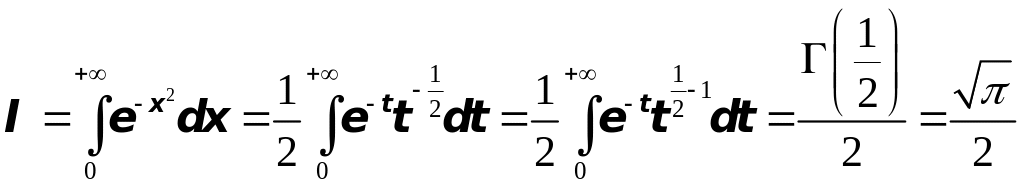Мы получили часто встречающийся в теории вероятностей интеграл, который называется интегралом Пуассона:

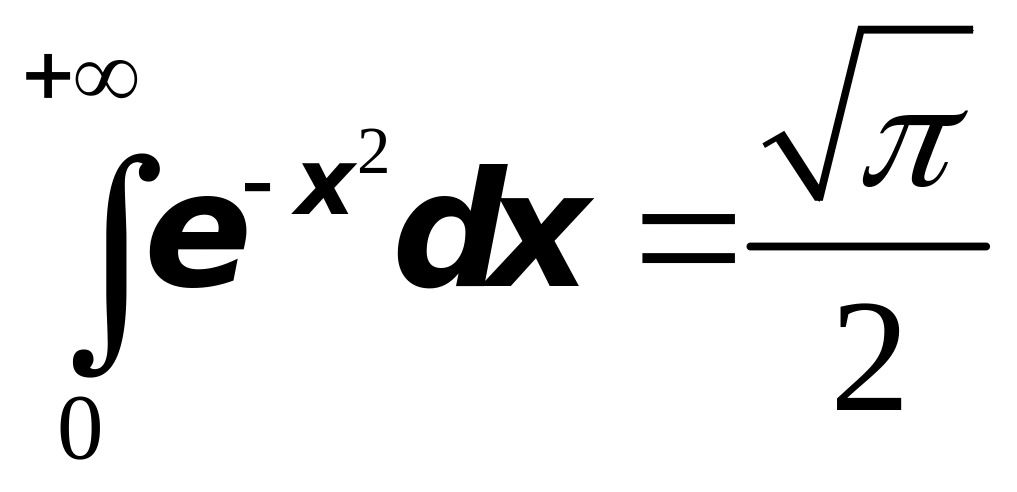(интеграл Пуассона).

Глава 3. Двойной и тройной интегралы §1. Двойной интеграл

Прежде чем дать определение двойного интеграла, сделаем несколько предварительных замечаний и определений.

Определение 1. Кривая называется простой кривой, если она распадается на конечное число частей, каждая из которых имеет уравнение вида или , при чём функции и непрерывны на некотором промежутке или соответственно .

В том случае, если кривая - простая, замкнутая, самонепересекающаяся кривая, лежащая в плоскости , то множество всех точек плоскости разбивается единственным образом на два связных множества. Мы будем в дальнейшем рассматривать области, ограниченные кривой . Точки, лежащие на контуре , мы будем считать принадлежащими области , которую ограничивает этот контур, т.е. будем рассматривать замкнутую область , ограниченную простым самонепересекающимся контуром .

Мы будем рассматривать в дальнейшем простые области, понимая под этим области, ограниченные простыми кривыми и такие, что любая прямая, параллельная координатным осям, пересекает границу области не более, чем в двух точках (рис. 1).

рис 1 рис 2

рис 3 рис 4

Естественно, что к числу таких областей мы будем относить и области, которые можно разбить на конечное число областей указанного выше типа (рис. 2). Рассмотрим простую область (рис. 3), ограниченную кривой , и обозначим через - множество расстояний между точками и , лежащими на кривой . Наибольшее из расстояний между точками и будем называть в дальнейшем диаметром области . Дадим теперь строгое определение понятия площади области , ограниченной контуром (рис. 4).

Пусть есть некоторый прямоугольник со сторонами, параллельными координатным осям, содержащий контур целиком внутри себя, не задевая точек контура . Разобьём прямоугольник сетью прямых, параллельных координатным осям, на прямоугольники (ячейки). Наибольший из диаметров ячеек обозначим через и будем называть рангом дробления.

О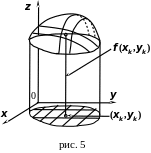 бозначим через сумму площадей ячеек, целиком лежащих в области и не задевающих контура , а через - сумму площадей ячеек, имеющих с областью или её контуром хотя бы одну общую точку. Очевидно, что . Если существует общий предел при условии, что число ячеек увеличивается, а ранг дробления стремится к нулю (т.е. ), то число называется площадью области , а сама область называется квадрируемой.

Рассмотрим теперь некоторую функцию , определённую в простой области , ограниченной контуром (рис 5). Дадим определение двойного интеграла.

Определение 2. Разобьём область сетью простых кривых произвольным образом на ячейки с площадями и диаметрами . Наибольший из диаметров обозначим через - ранг дробления.

В каждой частичной ячейке возьмём произвольную точку и вычислим в ней значение функции . Умножим затем на площадь соответствующей ячейки и просуммируем все такие произведения, т.е. составим сумму 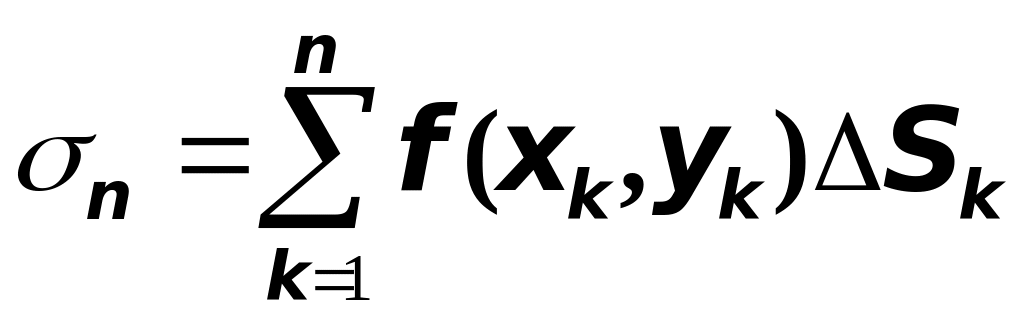, которая называется интегральной суммой или суммой Римана. Измельчая дальше дробление при условии, что ранг дробления , ищем предел последовательности интегральных сумм . Если этот предел существует и не зависит от способа дробления и выбора точек , то он называется двойным интегралом функции по области и обозначается так:

.

Сама подынтегральная функция при этом называется интегрируемой по области .

Итак, принимая во внимание приведённое выше рассуждение, мы можем коротко определить двойной интеграл от функции по области как предел последовательности интегральных сумм Римана, т.е.

.

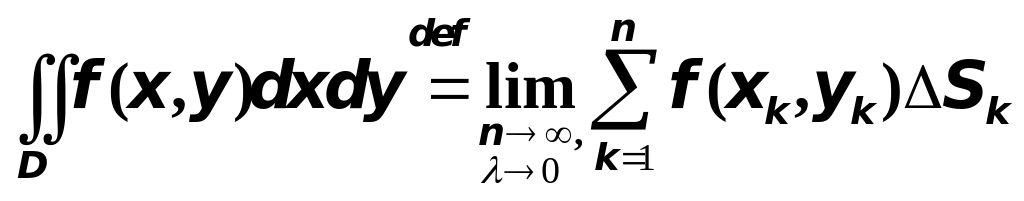Теорема существования двойного интеграла. Если подынтегральная функция непрерывна в каждой точке простой замкнутой области , то она в этой области интегрируема.

(Без доказательства).

Замечание. Можно доказать, что всякая интегрируемая в области функция ограничена в ней.