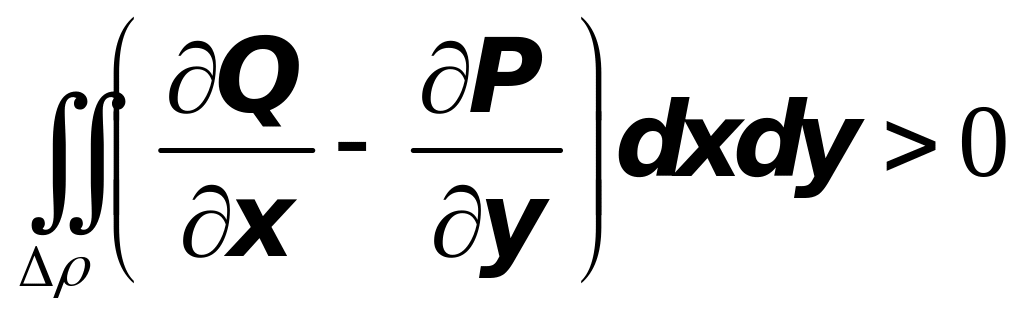,

следовательно, нашелся контур такой, что

.

Теорема 2. Если в каждой точке области функции и непрерывны и имеют непрерывные частные производные 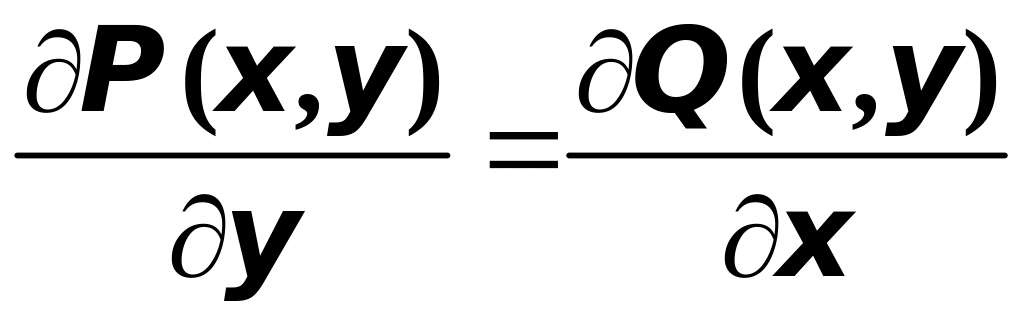, то выражение является полным дифференциалом непрерывной функции ,

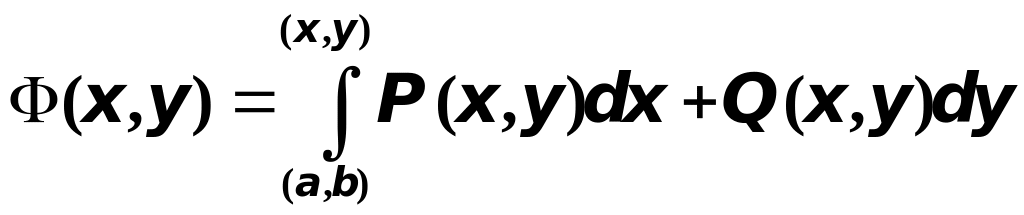т.е. .

Д оказательство. Пусть в каждой точке области выполнено условие (1). Закрепим точку и пусть - какая-нибудь точка области . Тогда зависит от точки , но не зависит от линии .

Это означает, что написанный интеграл является функцией переменных и . Обозначим через , тогда можно написать:

.

Попробуем продифференцировать функцию по переменной (рис. 10). Для этого, исходя из точки , дадим приращение , взяв его столь малым, чтобы отрезок , соединяющий точки и , целиком лежал в области , тогда будет

.

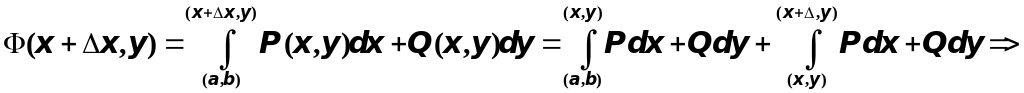
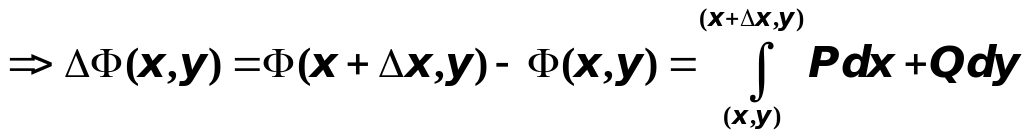Выразим криволинейный интеграл, стоящий в правой части, через определённый, учитывая, что на отрезке постоянен, т.е. , а . Тогда получим .

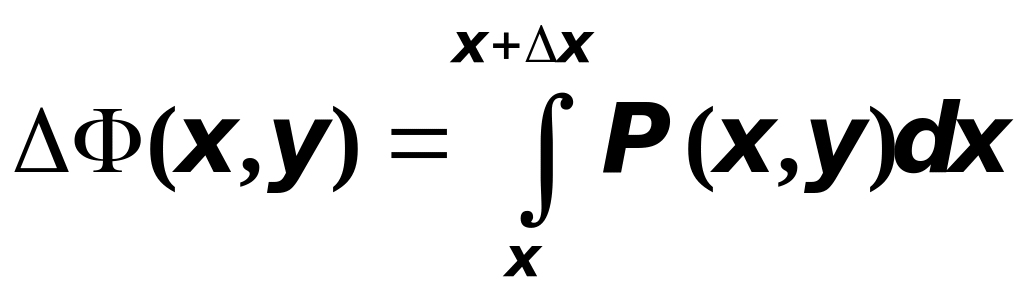Применим к определённому интегралу, стоящему справа, теорему о среднем, тогда будет , причём , тогда

.

Итак, мы получили

.

Аналогично можно доказать, что частная производная 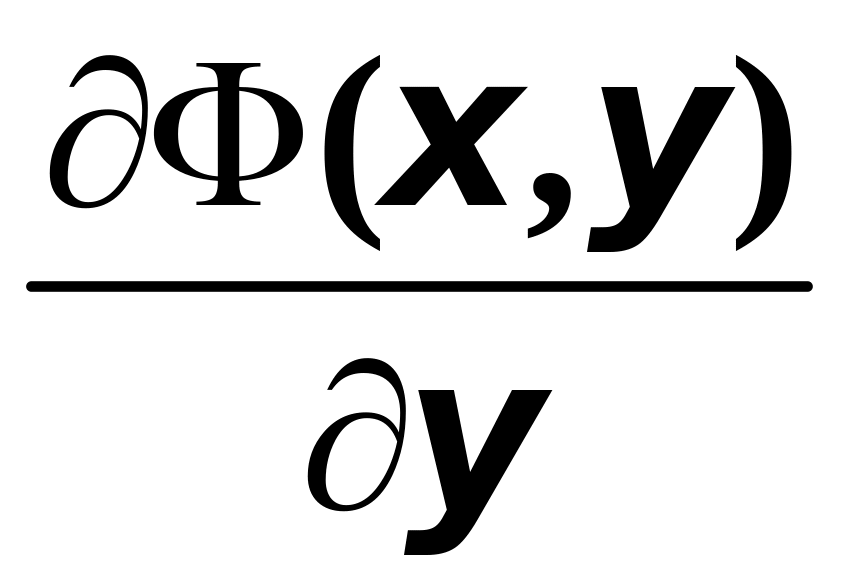также существует, причём 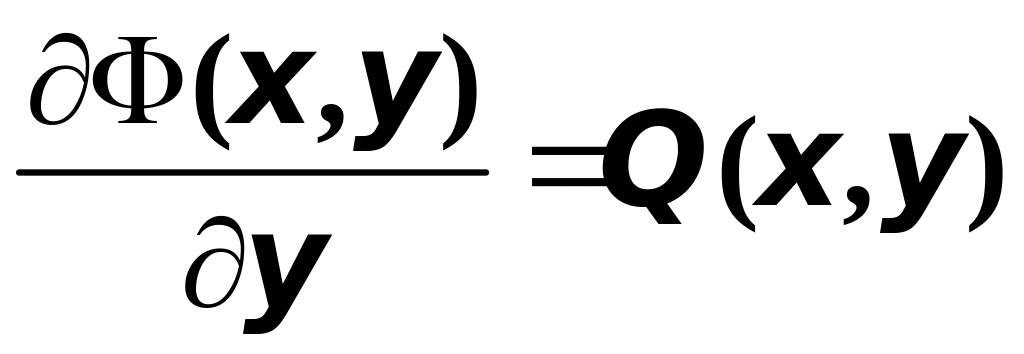. Следовательно, функция дифференцируема, причём .

Следствие. По предположению теоремы и непрерывны, следовательно, непрерывны и , а тогда непрерывна и сама функция .

Замечание. Доказанная теорема даёт нам возможность находить функцию по её полному дифференциалу с помощью криволинейного интеграла. Для этого нужно закрепить какую-нибудь точку , а затем, взяв произвольную точку , соединить их какой-нибудь простой кривой и вычислить , лишь бы только на этой кривой были выполнены условия теоремы существования криволинейного интеграла второго рода.

Доказанные выше две теоремы позволяют сформулировать такую общую теорему.

Теорема. Если в области заданы непрерывные функции и , имеющие непрерывные частные производные 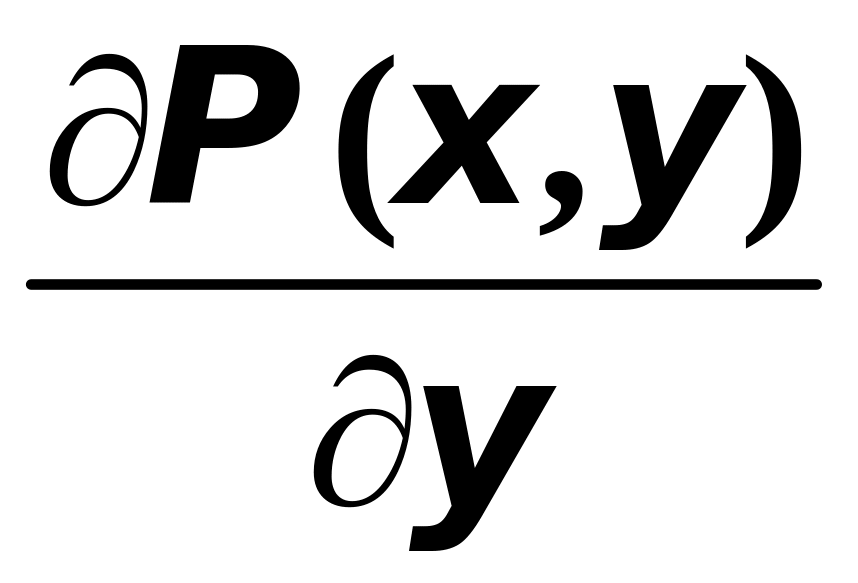и , то любые из следующих утверждений равносильны (т.е. из одного следует другое и наоборот):

1. зависит от точек и , но не от кривой .

2. Каков бы ни был замкнутый самонепересекающийся контур ,

.

3. Всюду в : .

4. Выражение есть полный дифференциал некоторой функции .

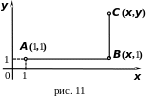
Пример. Убедиться, что выражение является полным дифференциалом некоторой функции и найти с её помощью криволинейный интеграл второго рода.

Решение. Прежде всего убедимся, что приведённое выражение является полным дифференциалом некоторой функции .

Обозначим , .

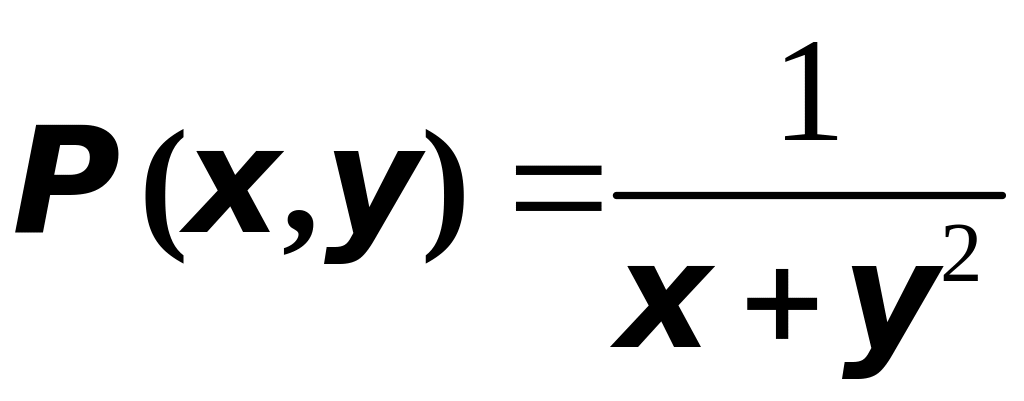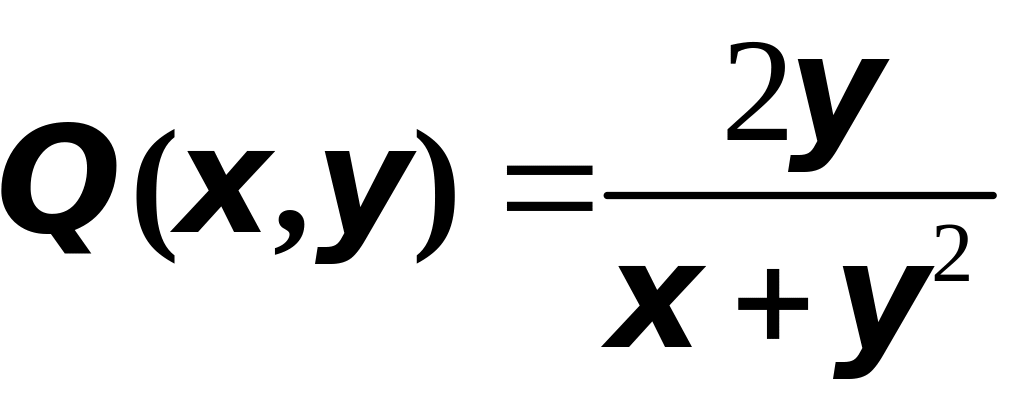Найдём .

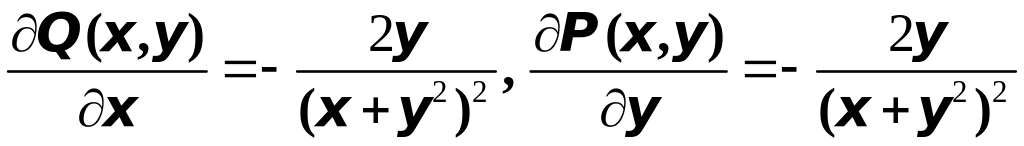Очевидно, что , т.е. действительно данное выражение является полным дифференциалом некоторой функции , т.е.

.

Найдём функцию , вычислив криволинейный интеграл по кривой , состоящей из двух отрезков: и , т.е. будет

.

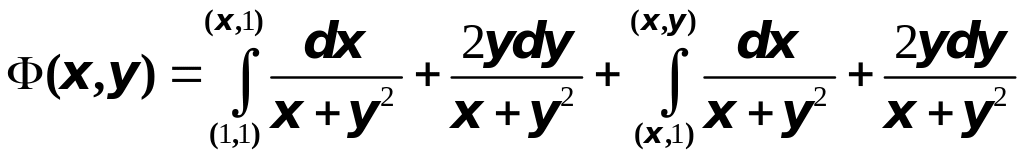Заметим, что на : , , ;

на : , , , следовательно:

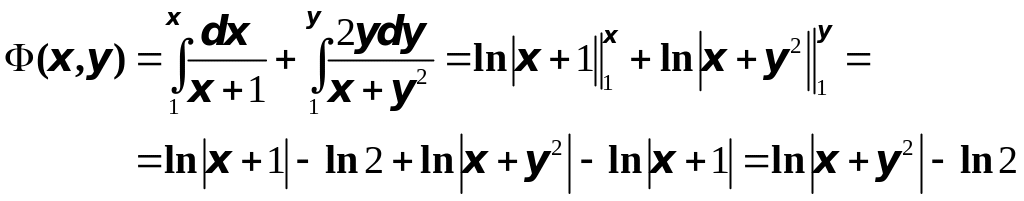
Ответ: , где - произвольная постоянная (рис. 11).

Заметим, что при решении данного примера мы не имеем права поместить точку в начало координат, т.к. в этом случае подынтегральная функция будет претерпевать разрыв, т.е. нарушится условие теоремы существования определённого интеграла.

Замечание 1. Заметим, что если при интегрировании дифференциального уравнения оказывается, что выполнено условие , то это говорит о том, что левая часть данного дифференциального уравнения представляет собой полный дифференциал некоторой функции , т.е. .

В этом случае дифференциальное уравнение называется обыкновенным дифференциальным уравнением в полных дифференциалах.

Очевидно, что можно легко найти общий интеграл этого уравнения, а именно: , а функция находится, как показано выше, с помощью криволинейного интеграла второго рода, т.е.

.

Замечание 2. Можно доказать, что для того, чтобы криволинейный интеграл

в некоторой области не зависел от пути интегрирования, необходимо, чтобы в каждой точке этой области выполнялись условия

, ,

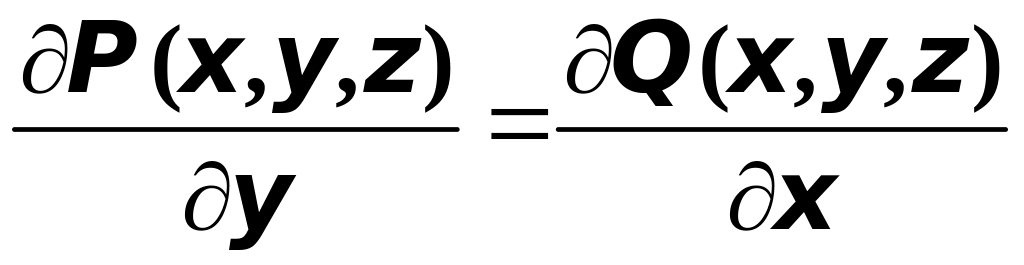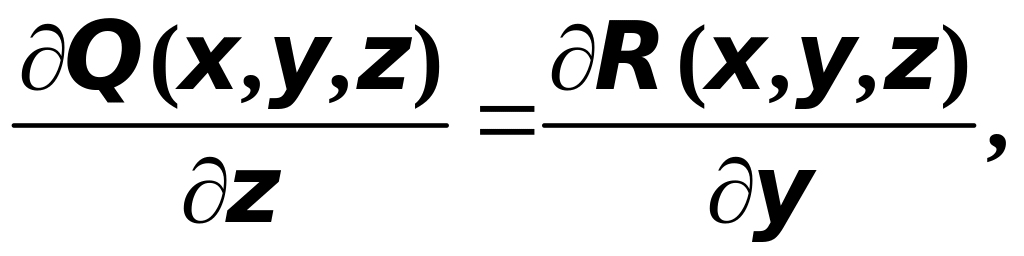
при этом функции , и предполагаются непрерывными и имеющими непрерывные указанные частные производные всюду в , а на кривой выполнены условия теоремы существования криволинейного интеграла второго рода.

Глава V. Поверхностные интегралы

§ 1. Поверхностные интегралы I рода

Определение. Пусть - квадрируемая поверхность, в каждой точке которой определена функция .

Разобьём поверхность сетью простых кривых на ячейки , ,…, с площадями и диаметрами . Наибольший из диаметров частичных ячеек обозначим через и будем называть его рангом дробления.

В каждой частичной ячейке возьмём произвольную точку и вычислим в ней значение функции . Умножим на площадь ячейки и составим интегральную сумму

.

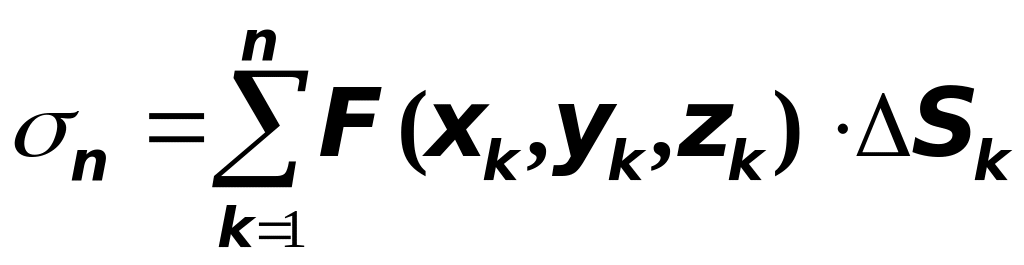Измельчая дробление таким образом, чтобы ранг дробления стремился к нулю, будем искать предел .

Если этот предел существует и не зависит от способа разбиения поверхности на ячейки и выбора точек , то он называется поверхностным интегралом первого рода от функции по поверхности и обозначается так:

.

Теорема существования поверхностного интеграла первого рода.

Если поверхность задана уравнением , причём функция определена и непрерывна в простой области плоскости и имеет в этой области непрерывные частные производные и и если в каждой точке поверхности функция непрерывна, то тогда поверхностный интеграл первого рода от функции существует и выражается через двойной интеграл так:

.

(без доказательства).

Не будем перечислять свойства поверхностного интеграла первого рода, т.к. они достаточно очевидны.

Пример. В каждой точке поверхности , лежащей в первом октанте, уравнение которой , распределена масса с плотностью , где . Вычислить массу пластинки.

Решение. , ,

.

Следовательно, масса

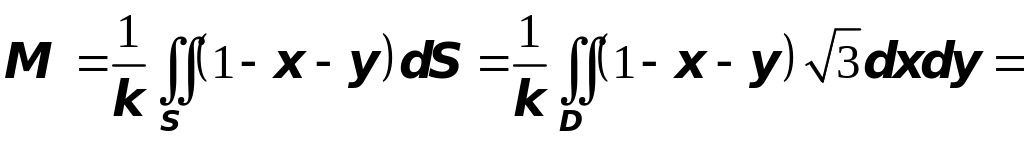
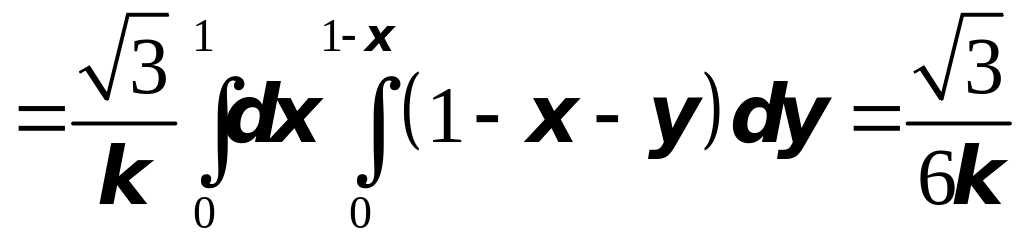кв. ед.

§ 2. Двухсторонние и односторонние поверхности. Сторона поверхности.

В озьмём некоторую поверхность и рассмотрим нормаль к этой поверхности в точке . Зафиксируем на нормали одно из двух возможных направлений (рис. 1).

Возьмём на поверхности некоторый контур, не пересекающий границы поверхности . Если мы будем перемещать основание нормали в направлении , то нормаль,

обойдя этот контур, вернётся к точке и займёт либо исходное положение , либо перевёрнутое .

Если на поверхности нет ни одного контура, который переворачивал бы нормаль после его обхода, то такая поверхность называется двухсторонней, а если есть хотя бы один контур, переворачивающий нормаль, то такая поверхность называется односторонней.

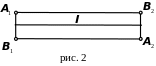
Примером односторонней поверхности может служить лист Мёбиуса, который легко можно изготовить, взяв полоску бумаги (рис. 2) и соединив точку с точкой , точку с точкой .

Нетрудно заметить, что обход контура переворачивает нормаль.

Определение. Совокупность точек двухсторонней поверхности вместе с соответствующими направлениями нормалей, непрерывно переходящих друг в друга при перемещении основания нормали по поверхности, не пересекая его границы, называют стороной поверхности.

В соответствии с приведённым определением можно сделать вывод, что двухсторонняя поверхность имеет две стороны поверхности: верхнюю и нижнюю, а односторонняя поверхность не имеет ни одной стороны поверхности.

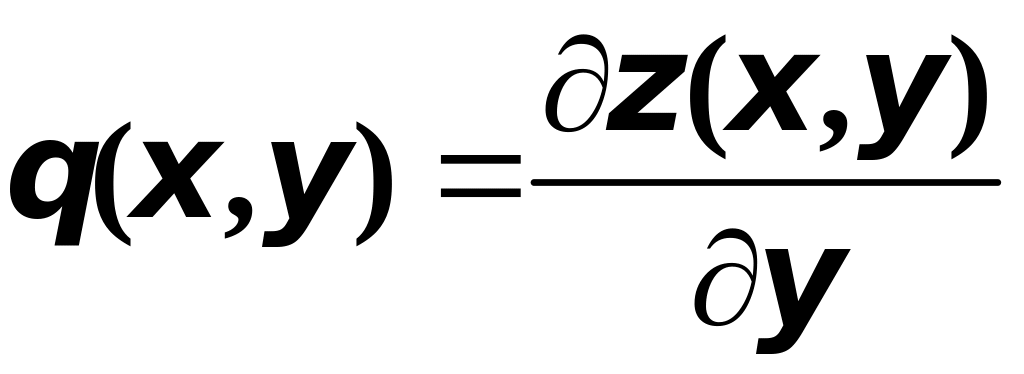Причём, если двухсторонняя поверхность задана уравнением , где и частные производные и непрерывны в области плоскости , то для верхней стороны поверхности направляющие косинусы нормали определяются выражениями

, , ,

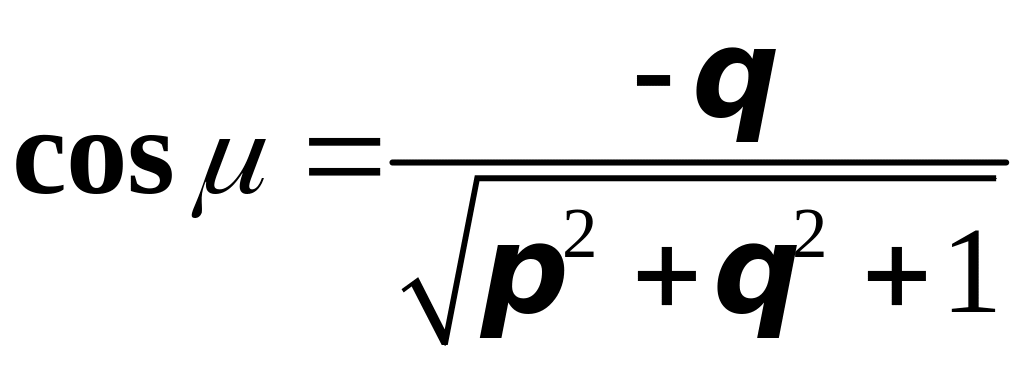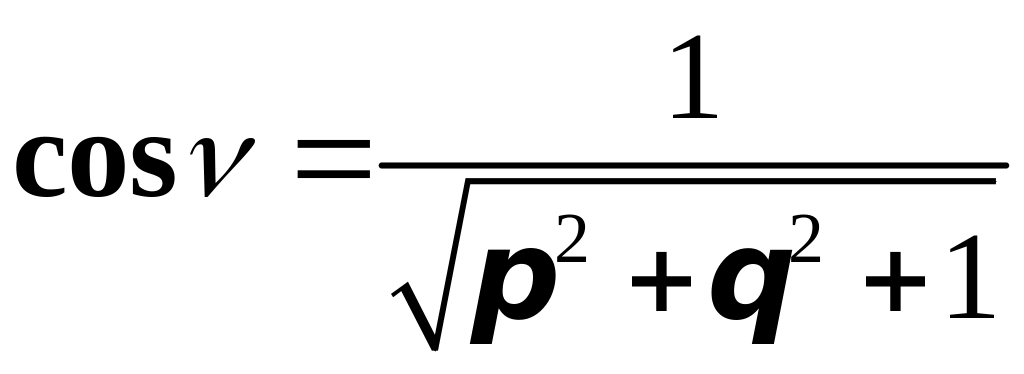а для нижней стороны поверхности соответственно

, , .
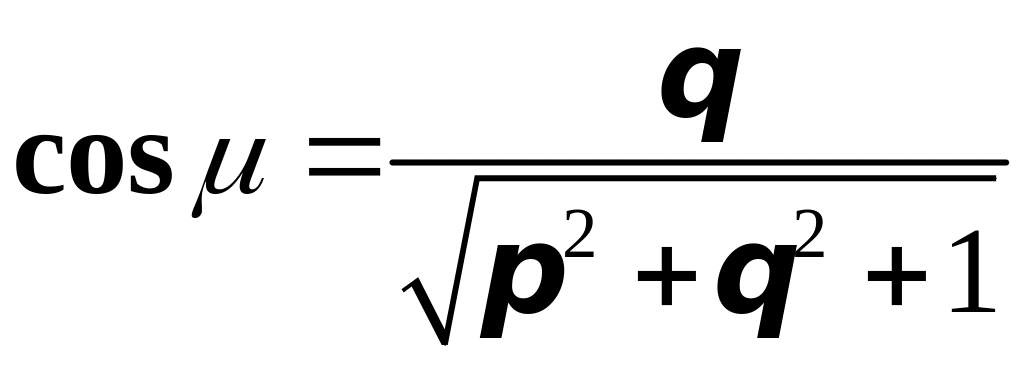
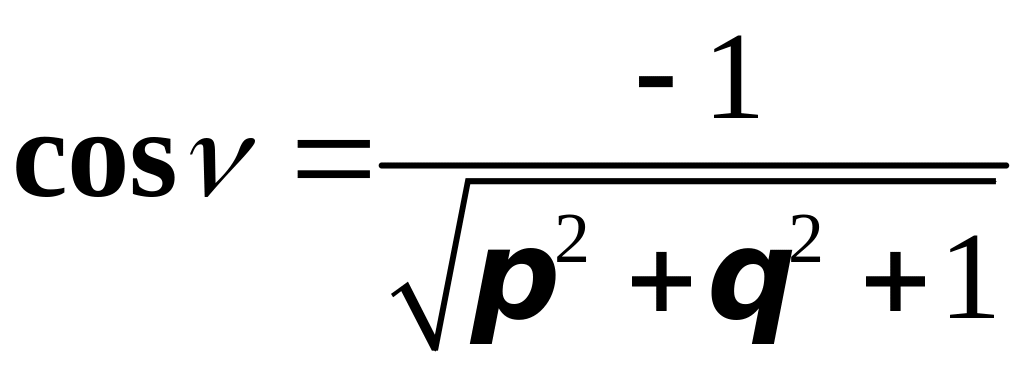