
- •§ 2. Криволинейные интегралы второго рода
- •1. Определение криволинейного интеграла второго рода
- •2. Теорема существования криволинейного интеграла
- •3. Свойства криволинейного интеграла второго рода
- •4. Связь криволинейных интегралов первого и второго рода
- •5. Вычисление работы с помощью криволинейного интеграла
- •§ 3. Формула Грина
- •§ 4. Криволинейные интегралы, не зависящие от пути интегрирования
н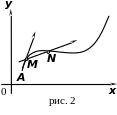 аправлением
кривой. Действительно, пусть при движении
по кривой от
аправлением
кривой. Действительно, пусть при движении
по кривой от
![]() к
к
![]() точка
точка
![]() предшествует точке
предшествует точке
![]() ,
тогда будем считать, что секущая,
проходящая от
к
,
имеет направление, совпадающее с
направлением кривой
,
тогда будем считать, что секущая,
проходящая от
к
,
имеет направление, совпадающее с
направлением кривой
![]() .
Касательная
.
Касательная
![]() есть предельное положение секущей при
условии, что
есть предельное положение секущей при
условии, что
![]() .
Тогда направление с секущей переходит
на касательную, и про такую касательную
говорят, что она имеет направление,
совпадающее с направлением кривой
.
.
Тогда направление с секущей переходит
на касательную, и про такую касательную
говорят, что она имеет направление,
совпадающее с направлением кривой
.
Найдём
работу силы
![]() по перемещению материальной точки
из точки
в точку
вдоль кривой (рис. 3).
по перемещению материальной точки
из точки
в точку
вдоль кривой (рис. 3).
Р азобьём
кривую
произвольным образом на
азобьём
кривую
произвольным образом на
![]() частей и будем считать, что каждый
частей и будем считать, что каждый
![]() -й
участок кривой - прямолинейный отрезок,
длина которого
-й
участок кривой - прямолинейный отрезок,
длина которого
![]() ,
сила
на каждом таком участке постоянная по
величине и направлению, и угол между
силой
,
сила
на каждом таком участке постоянная по
величине и направлению, и угол между
силой
![]() и участком кривой равен
и участком кривой равен
![]() .
Тогда элементарная работа силы
на рассматриваемом участке
.
Тогда элементарная работа силы
на рассматриваемом участке
![]() .
Отсюда вся работа
.
Отсюда вся работа
![]() .
.
§ 2. Криволинейные интегралы второго рода
1. Определение криволинейного интеграла второго рода
Пусть
в плоскости
![]() лежит кривая
,
в каждой точке которой определена
функция
лежит кривая
,
в каждой точке которой определена
функция
![]() (рис. 1).
(рис. 1).
Разобьём
кривую
произвольным образом точками
![]()
![]() ,
,
![]() ,
следующими друг за другом, на
частей, пусть
,
следующими друг за другом, на
частей, пусть
![]() ,
,
![]() ,
…,
,
…,
![]() - диаметры дуг
- диаметры дуг
![]() ,
,
![]() ,
наибольший из диаметров
,
наибольший из диаметров
![]() ,
равный
,
равный
![]() ,
есть ранг дробления.
,
есть ранг дробления.
На
каждой дуге
![]() возьмём произвольную точку
возьмём произвольную точку
![]() и вычислим в ней значение функции
и вычислим в ней значение функции
![]() ,
т.е. составим произведение
,
т.е. составим произведение
![]() .
.
Просуммируем все такие произведения, т.е. составим интегральную сумму (сумму Римана):
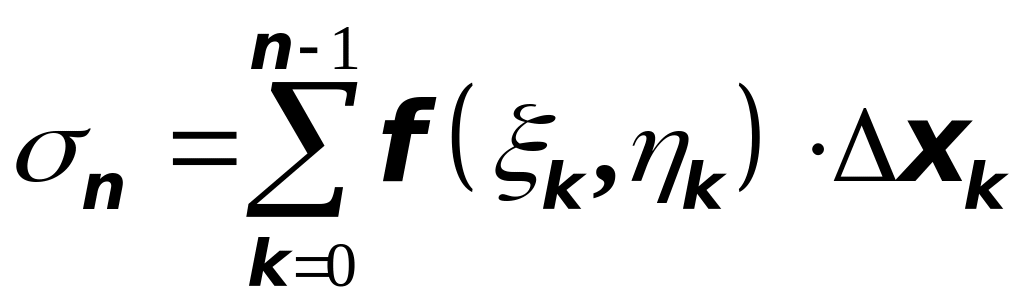 .
.
Измельчая дробление и устремляя ранг дробления к нулю, ищем предел
![]() .
.
Если этот предел существует, то он называется криволинейным интегралом второго рода от функции по кривой и обозначается так:
![]() .
.
Итак, короче:
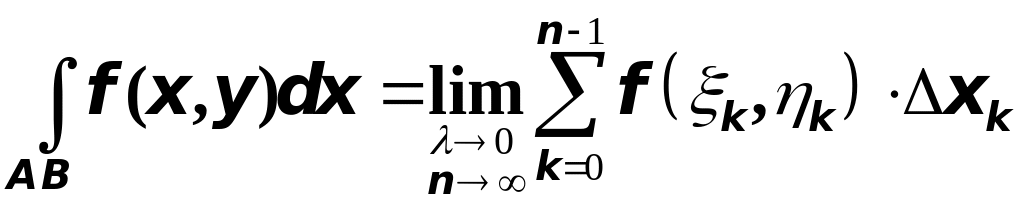 .
.
Определение
относится к плоской кривой. Точно так
же определяется интеграл по пространственной
кривой
![]() .
.
Аналогично
определяются интегралы
![]() и
и
![]() .
Сумму интегралов по кривой
обозначают так:
.
Сумму интегралов по кривой
обозначают так:
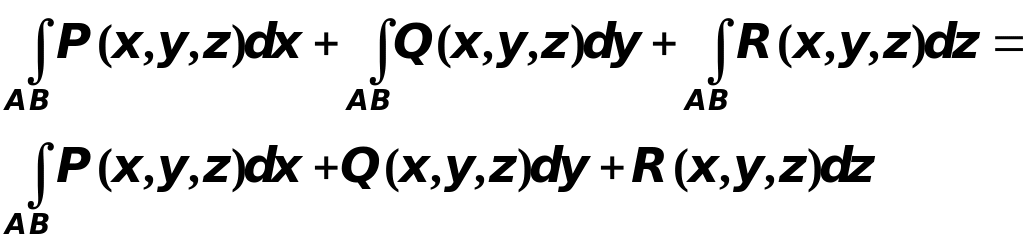
Всё
сказанное не исключает случая, когда
точка
совпадает с точкой
,
т.е. кривая
представляет собой замкнутый контур
![]() ,
в этом случае криволинейный интеграл
второго рода обозначается так:
,
в этом случае криволинейный интеграл
второго рода обозначается так:
![]() ,
,
причём безразлично, в какой точке следует начать движение по контуру. Следует заметить, что если - есть плоский замкнутый самонепересекающийся контур, то у такого контура различают положительное и отрицательное направление обхода, а именно: за положительное направление обхода принимают такое направление, при котором область, ограниченная контуром , остается слева, если наблюдатель движется по контуру. В таком случае, если - пространственная кривая, то направление обхода контура оговаривается особо. Иногда для интегралов по замкнутому самонепересекающемуся контуру употребляют такие обозначения:
![]() и
и
![]() .
.
2. Теорема существования криволинейного интеграла
второго рода
Теорема.
Пусть кривая
задана уравнениями
![]() ,
,
![]() ,
где
,
где
![]() и
и
![]() непрерывны на промежутке
непрерывны на промежутке
![]() ,
причём
,
причём
![]() также существует и непрерывна на
,
причём, когда параметр
также существует и непрерывна на
,
причём, когда параметр
![]() возрастает от
возрастает от
![]() до
до
![]() ,
то кривая
(или контур
)
описывается в одном и том же направлении
от
до
.
,
то кривая
(или контур
)
описывается в одном и том же направлении
от
до
.
Пусть также в каждой точке кривой задана непрерывная функция .
Тогда криволинейный интеграл второго рода от функции по кривой существует и выражается через определённый интеграл так:
 .
.
Частный
случай. Если кривая
задана уравнением
![]() ,
где
,
где
![]() - непрерывная на промежутке
- непрерывная на промежутке
![]() функция, и если в каждой точке кривой
задана непрерывная функция
,
то тогда криволинейный интеграл второго
рода
существует и выражается через определенный
интеграл так:
функция, и если в каждой точке кривой
задана непрерывная функция
,
то тогда криволинейный интеграл второго
рода
существует и выражается через определенный
интеграл так:
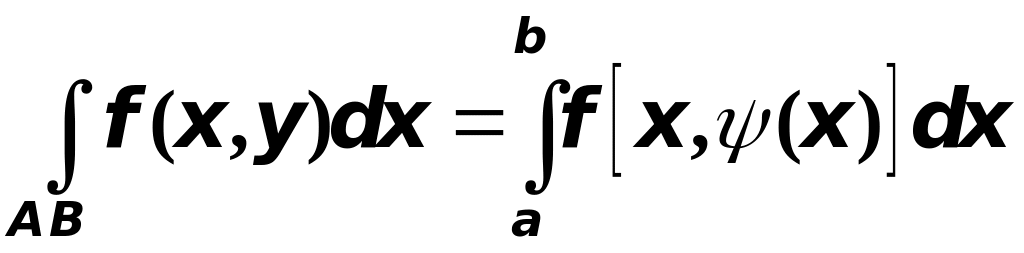 .
.
3. Свойства криволинейного интеграла второго рода
Остановимся на некоторых свойствах и применениях криволинейного интеграла второго рода, причём не будем упоминать и доказывать свойства, которые очевидны.
1. При определении криволинейного интеграла второго рода нужно различать начало и конец пути интегрирования, а именно:
![]() .
.
Это свойство станет очевидным, если для одного и того же способа разбиения составить интегральные суммы для интегралов, стоящих в левой и прямой части равенства.
2. В том случае, если кривая замкнута, т.е. представляет собой замкнутый контур , то
![]() ,
,
т.е. изменение направления обхода контура меняет знак интеграл на противоположный.
3. Если
функция
интегрируема на кривой
и если точка
![]() разбивает кривую на два участка
разбивает кривую на два участка
![]() и
и
![]() ,
то
,
то
![]() .
.
Для доказательства этого свойства достаточно составить интегральную сумму, а точку включить в число точек дробления.
4.
Очевидно, что если кривая
есть прямолинейный отрезок, перпендикулярный
оси
![]() ,
то при любой
интеграл
существует и равен нулю.
,
то при любой
интеграл
существует и равен нулю.
