4. Связь криволинейных интегралов первого и второго рода

Р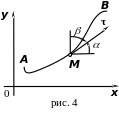 ассмотрим интеграл , где - непрерывная функция в каждой точке кривой , а кривая задана уравнением , причём непрерывна и имеет непрерывную производную на промежутке , где и

является абсциссой точки ,

- абсциссой точки (рис. 4)

При выполнении таких условий кривая в каждой точке имеет касательную. Мы будем рассматривать касательную, имеющую направление, совпадающее с направлением кривой . Обозначим через угол между положительным направлением касательной и осью . В силу геометрического смысла производной следует, что , а тогда

.

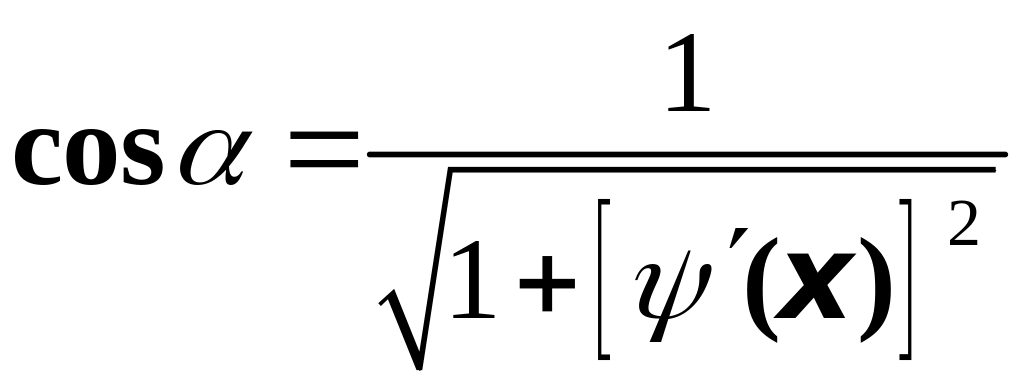Интеграл мы можем записать так:

.

Перейдём в правой части к определённому интегралу:

.

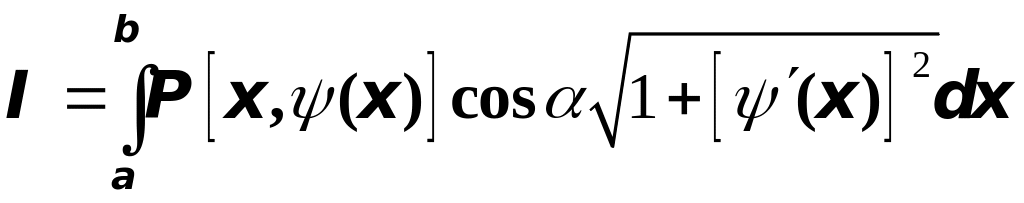Точно такому же определённому интегралу равен криволинейный интеграл первого рода

,

т.е. .

Окончательно получаем

.

Совершенно аналогично можно доказать и такую формулу:

,

где - угол между положительным направлением касательной к осью .

Скатывая почленно две последние формулы, получим соотношение, устанавливающее связь между криволинейными интегралами первого и второго рода по кривой , лежащей в плоскости :

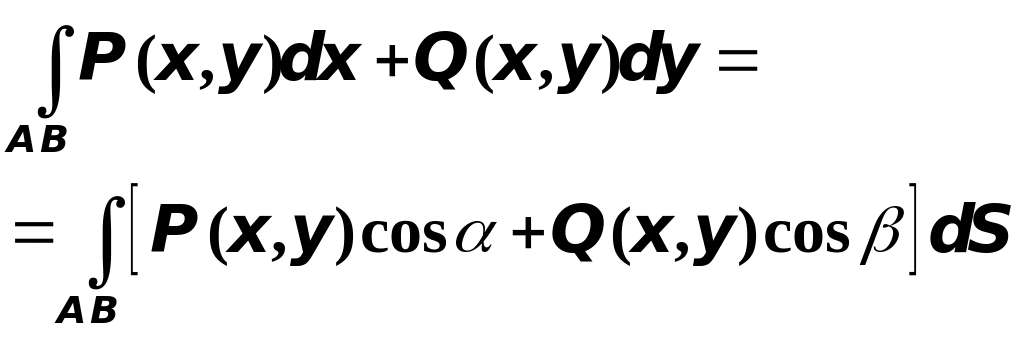
Между левой и правой частям равенства здесь такое согласование: следа интеграл вычисляется по кривой от к , а справа через и обозначены углы касательной, направление которой совпадает с направлением кривой , с координатными осями.

Если - пространственная кривая, , , - углы касательной, совпадающей по направлению с кривой , с координатными осями , и соответственно, то справедливо такое соотношение:

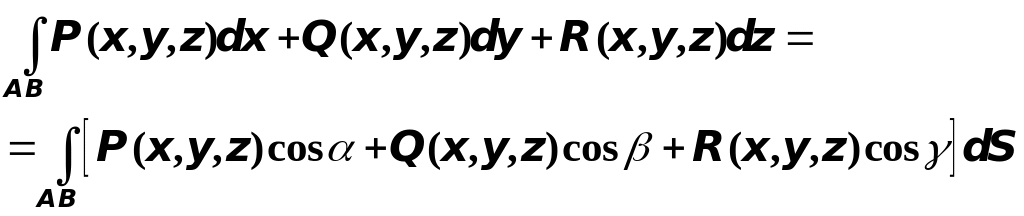
5. Вычисление работы с помощью криволинейного интеграла

М ы получили ранее выражение для работы силы по перемещению материальной точки по кривой через криволинейный интеграл первого рода: .

Здесь - угол между вектором и касательной, направление которой совпадает с направлением кривой .

Найдём выражение для этой работы с помощью криволинейного интеграла второго рода (рис. 5). Пусть - угол между направлением касательной и осью , - угол между вектором и осью , тогда ясно, что

.

Обозначим через и проекции силы на координатные оси. Очевидно, что

,

кроме того,

,

тогда

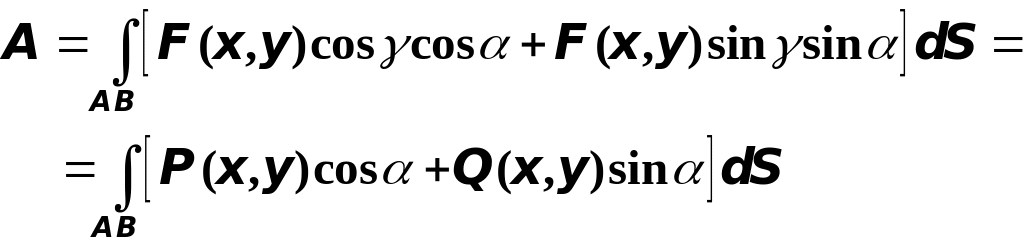
Принимая во внимание формулу, устанавливающую связь между криволинейными интегралами первого и второго рода, получим окончательно

.

Итак, всякий криволинейный интеграл второго рода вида

можно истолковать как работу силы, имеющей своими проекциями на координатные оси и , по перемещению материальной точки вдоль кривой из точки в точки .

§ 3. Формула Грина

Пусть задана некоторая область , ограниченная снизу кривой , сверху - кривой , а с боков - отрезками и , параллельными

о си (рис. 6), и пусть в этой области определена непрерывная функция , имеющая непрерывную частную производную .

Вычислим

.

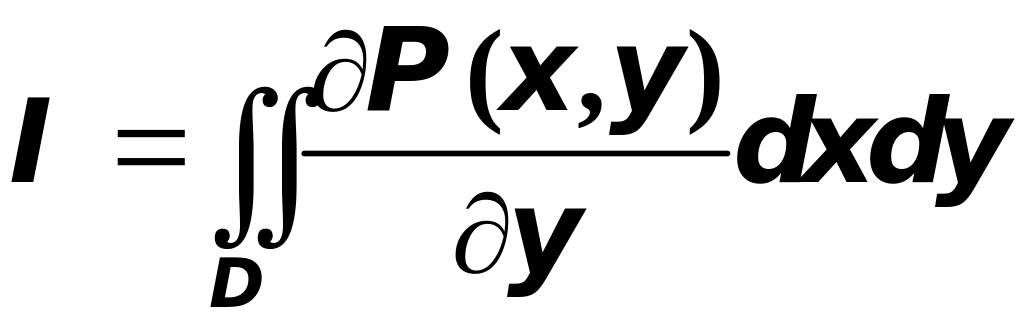Переходя к повторному интегралу, получим

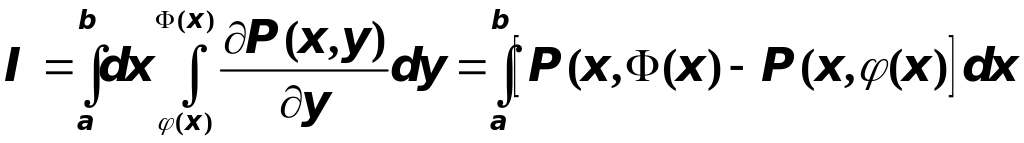
С другой стороны, интеграл по контуру области :

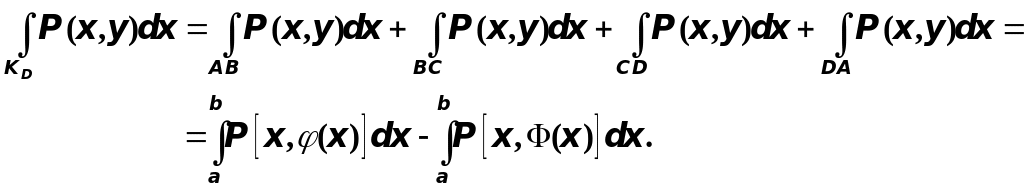
Правые части двух последних формул отличаются только знаком, следовательно,

.

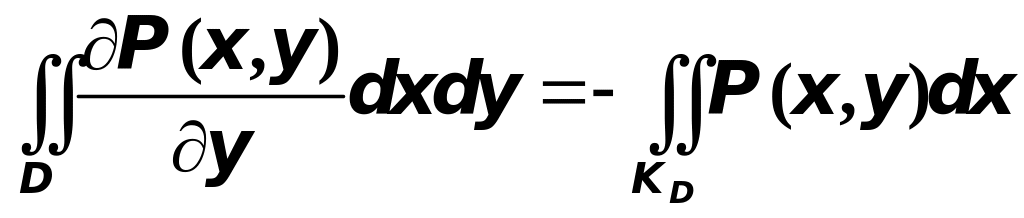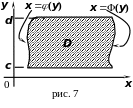
Полученная формула называется малой формулой Грина. Можно доказать, что она справедлива и для области, изображенной на рис. 7.

Нетрудно доказать также, что эта формула справедлива для любой области, распадающейся на конечное число частей, изображенных на рис. 6 и рис. 7.

Если в области определена и непрерывна функция , имеющая непрерывную частную производную , то совершенно аналогично можно доказать вторую малую формулу Грина:

.

Складывая почленно обе малые формулы Грина, получим формулу

.

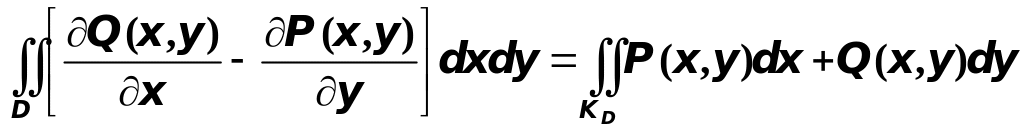Эта формула называется большой формулой Грина или просто формулой Грина. Она устанавливает связь между двойным интегралом по области и криволинейным интегралом по контуру этой области.

Замечание (о вычислении площади области с помощью криволинейного интеграла). Положим в формуле Грина , тогда получим

.

При таких значениях функции и интеграл, стоящий в левой части формулы Грина, даёт нам удвоенную площадь области , откуда следует

.

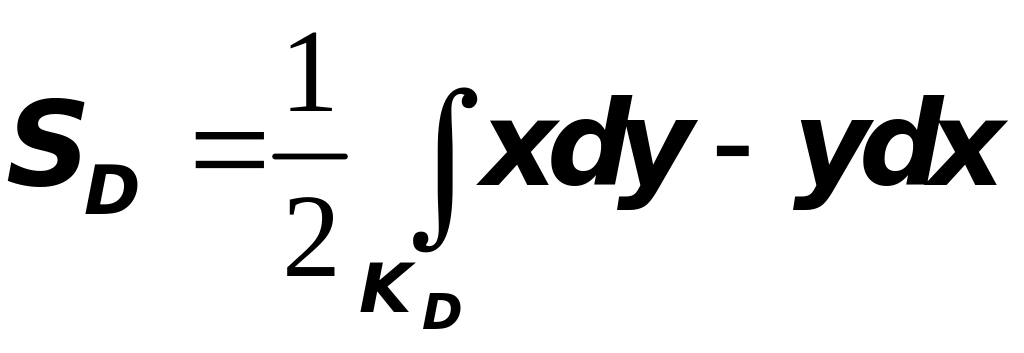По этой формуле можно вычислить площадь области , ограниченной контуром .

Пример. Вычислить площадь эллипса

Решение. Очевидно, что когда параметр изменяется от до , точка обегает полный контур эллипса в положительном направлении. Учитывая, что , получим

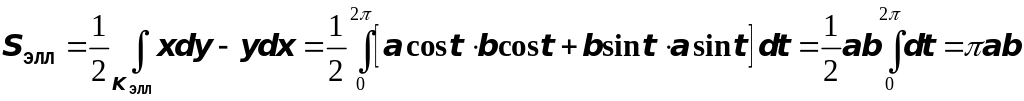кв. ед.