
- •3. Вычисление площади поверхности тела вращения
- •4. Вычисление объёмов
- •§4. Общая схема применения определённого интеграла
- •1. Методика применения определённого интеграла к решению практических задач.
- •2. Работа переменной силы
- •3. Давление на пластинку, погруженную вертикально в жидкость
- •4. Моменты. Центры масс плоских фигур.
- •5. Приложение определённого интеграла к
П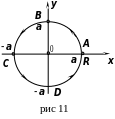 ример
6. Найти длину дуги окружности
радиуса
ример
6. Найти длину дуги окружности
радиуса
![]() ,
записав её уравнение в полярных
координатах (рис 11)
,
записав её уравнение в полярных
координатах (рис 11)
Решение. Напомним, что уравнение
окружности
радиуса
с центром в начале координат имеет вид
![]() .
Примем во внимание связь между декартовыми
и полярными координатами:
.
Примем во внимание связь между декартовыми
и полярными координатами:
![]()
(здесь
предполагается, что начало декартовых
координат совпадает с полюсом
![]() ,
а ось
,
а ось
![]() совпадает с полярной осью).
совпадает с полярной осью).
Тогда очевидно, что уравнение окружности
в полярных координатах:
![]() ,
причём, когда
,
причём, когда
![]() ,
текущая точка
,
текущая точка
![]() обегает контур окружности один раз
против часовой стрелки.
обегает контур окружности один раз
против часовой стрелки.
Имеем
![]() ,
тогда
,
тогда
![]() ,
следовательно
,
следовательно
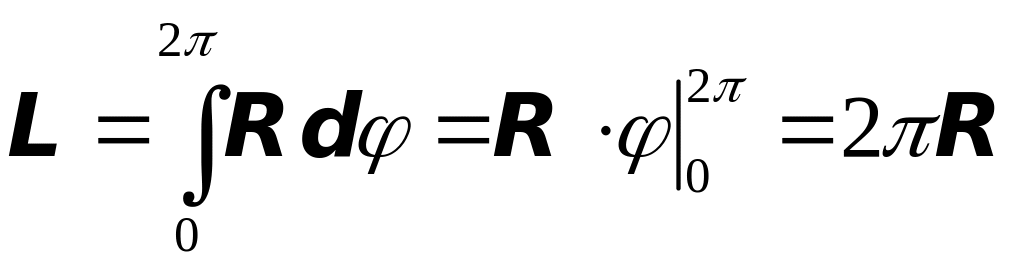 .
.
Итак, мы получили всем известную формулу
для вычисления длины дуги окружности
радиуса
:
![]() .
.
3. Вычисление площади поверхности тела вращения
Р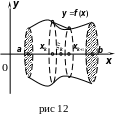 ассмотрим
на плоскости
ассмотрим
на плоскости
![]() некоторую кривую
некоторую кривую
![]() ,
заданную уравнением
,
заданную уравнением
![]() .
Пусть функция
.
Пусть функция
![]() и производная
и производная
![]() непрерывны на
непрерывны на
![]() .
От вращения кривой
вокруг оси
.
От вращения кривой
вокруг оси
![]() получается тело вращения, ограниченное
поверхностью вращения. По определению
будем считать площадью поверхности
вращения площадь поверхности, которая
получается от вращения ломаной линии
получается тело вращения, ограниченное
поверхностью вращения. По определению
будем считать площадью поверхности
вращения площадь поверхности, которая
получается от вращения ломаной линии
![]() ,
вписанной в кривую
(рис 12) при условии, что число точек
дробления бесконечно возрастает, а ранг
дробления
,
вписанной в кривую
(рис 12) при условии, что число точек
дробления бесконечно возрастает, а ранг
дробления
![]() при этом стремится к нулю.
при этом стремится к нулю.
От вращения хорды
![]() получим усечённый конус, боковая
поверхность которого
получим усечённый конус, боковая
поверхность которого
![]() ,
,
где
![]() .
.
Площадь поверхности вращения
![]() таким образом приблизительно равна
таким образом приблизительно равна
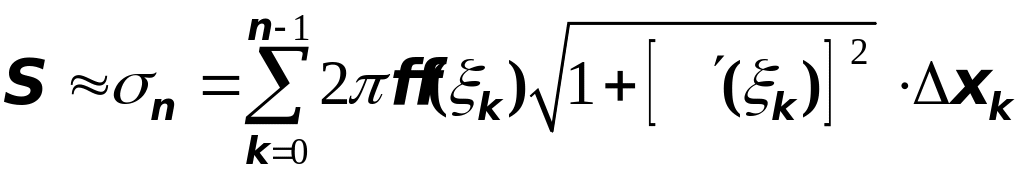
Измельчая дробление и устремляя ранг дробления к нулю, получим точное равенство
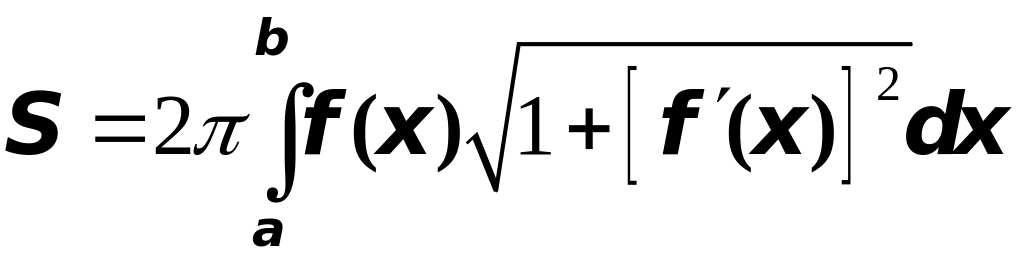
П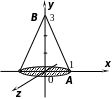 ример
7. Кривая
ример
7. Кривая
![]() вращается вокруг оси
вращается вокруг оси
![]() ,
найти площадь поверхности, ограниченной
плоскостью
,
найти площадь поверхности, ограниченной
плоскостью
![]() и получившейся поверхностью вращения.
и получившейся поверхностью вращения.
Р
рис 13![]() и
и
![]() ,
а интересующее нас тело есть конус (рис
12). Воспользуемся выведенной выше
формулой, заменив в ней естественным
образом переменную
,
а интересующее нас тело есть конус (рис
12). Воспользуемся выведенной выше
формулой, заменив в ней естественным
образом переменную
![]() на переменную
на переменную
![]() .
.
Получим
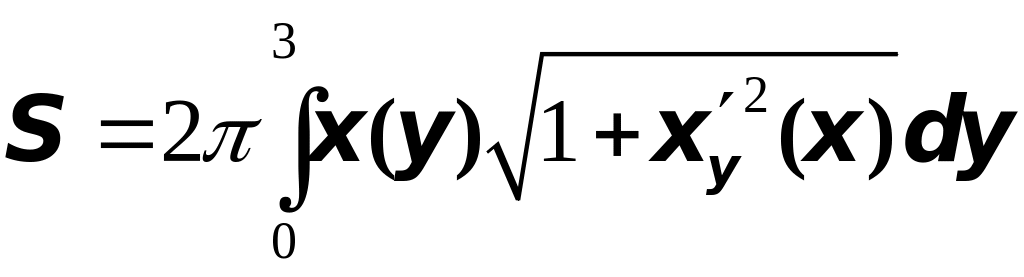 .
.
Подставим сюда
![]() ,
тогда будет
,
тогда будет
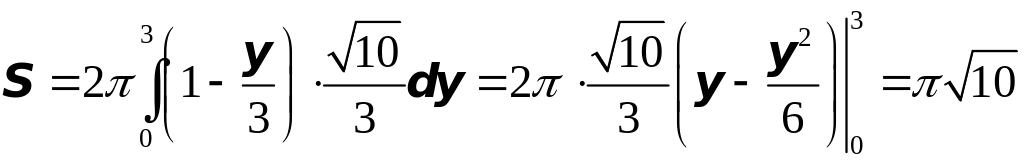 ,
,
что легко проверить, вычислив площадь боковой поверхности конуса
![]()
Итак
![]() кв.ед..
кв.ед..
4. Вычисление объёмов
Р
рис 14


![]()

![]()
![]()
![]()
![]()
![]()
 ассмотрим
некоторое тело, вытянутое вдоль оси
ассмотрим
некоторое тело, вытянутое вдоль оси
![]() и допустим, что мы знаем площадь сечения
этого тела любой плоскостью
и допустим, что мы знаем площадь сечения
этого тела любой плоскостью
![]() .
Обозначим площадь этого сечения через
.
Обозначим площадь этого сечения через
![]() .
Разобьём отрезок
произвольным образом на
.
Разобьём отрезок
произвольным образом на
![]() частей точками
частей точками
![]() .
.
На каждом частичном участке
![]() возьмём произвольную точку
.
Площадь этого сечения
возьмём произвольную точку
.
Площадь этого сечения
![]() .
Элементарный объём
.
Элементарный объём
![]() ,
тогда очевидно, что объём рассматриваемого
тела
,
тогда очевидно, что объём рассматриваемого
тела
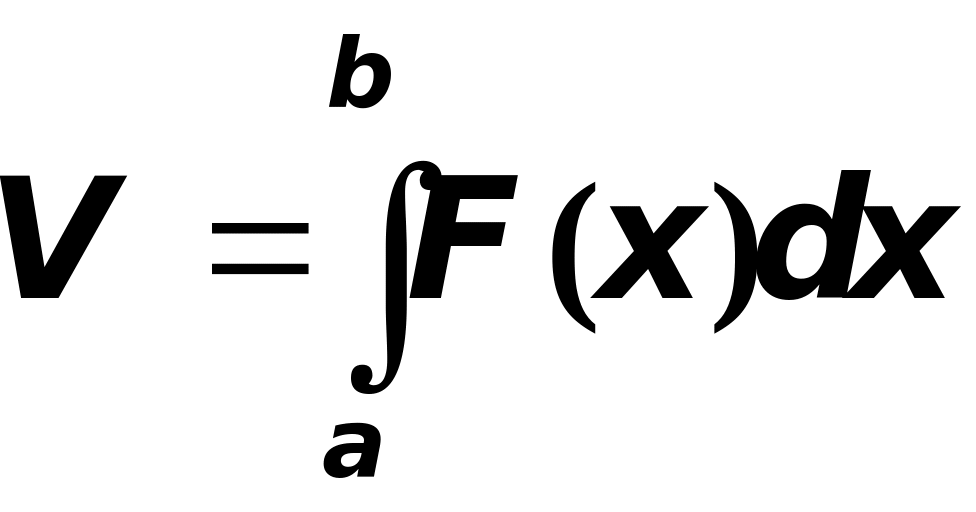 .
.
В частности, отсюда нетрудно получить
формулу объёма тела вращения, которая
получается от вращения
![]() вокруг оси
(
предполагается непрерывной на промежутке
).
Действительно, в этом случае площадь
сечения представляет собою круг радиуса
вокруг оси
(
предполагается непрерывной на промежутке
).
Действительно, в этом случае площадь
сечения представляет собою круг радиуса
![]() ,
следовательно площадь сечения равна
,
следовательно площадь сечения равна
![]() .
А тогда объём тела вращения
.
А тогда объём тела вращения
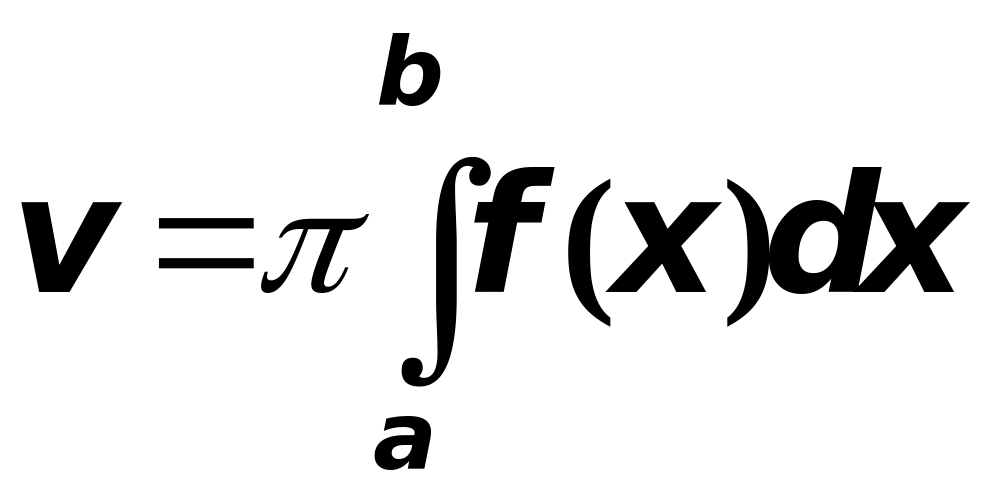
Пример 8. Найти объём шара радиуса .
Решение.
На шар будем смотреть как
на тело вращения. Здесь
![]() .
Тогда
.
Тогда
 .
.
Получим известную формулу для объёма шара радиуса :
![]() куб.ед..
куб.ед..
§4. Общая схема применения определённого интеграла
1. Методика применения определённого интеграла к решению практических задач.
Выше мы рассмотрели различные случаи применения определённого интеграла для решения геометрических задач. Но область применения определённого интеграла очень обширна и независимо от конкретного содержания задачи приходится действовать по вполне определённой схеме.
Пусть
требуется определить некоторую постоянную
величину
![]() ,
связанную промежутком
.
Эту величину мы будем предполагать
аддитивной, т.е. такой, что разложение
отрезка
точкой
,
связанную промежутком
.
Эту величину мы будем предполагать
аддитивной, т.е. такой, что разложение
отрезка
точкой
![]()
![]() на части
на части
![]() и
и
![]() влечёт за собой разложение на
соответствующие части величины
,
причём значение величины
,
соответствующее всему отрезку
,
равно сумме её значений, соответствующих
отрезкам
и
.
влечёт за собой разложение на
соответствующие части величины
,
причём значение величины
,
соответствующее всему отрезку
,
равно сумме её значений, соответствующих
отрезкам
и
.
Переходя к решению задачи по определению величины , разложим отрезок при помощи точек
![]()
на частей
![]()
![]() - длина
- длина
![]() -го
частичного промежутка,
- ранг дробления. В соответствии с
разложением промежутка
величина
разложится на
слагаемых
-го
частичного промежутка,
- ранг дробления. В соответствии с
разложением промежутка
величина
разложится на
слагаемых
![]() :
:
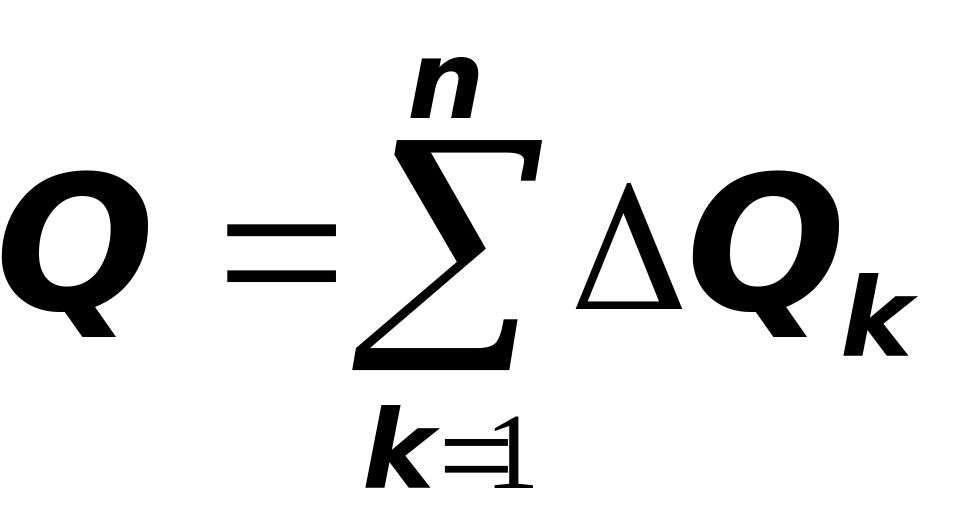 .
.
Допустим
теперь, что существует такая функция
![]() ,
что "элементарное" слагаемое
,
что "элементарное" слагаемое
![]() ,
соответствующее промежутку
,
соответствующее промежутку
![]() длины
длины
![]() ,
приближенно может быть записано в виде
,
приближенно может быть записано в виде
![]() ,
,
где
лежит между
![]() и
,
причём ошибка этого равенства при
бесконечно малом ранге дробления
и
,
причём ошибка этого равенства при
бесконечно малом ранге дробления
![]() будет бесконечно малой, порядка высшего,
чем
,
т.е.
будет бесконечно малой, порядка высшего,
чем
,
т.е.
![]() .
.
В этом случае для получается приближённое выражение
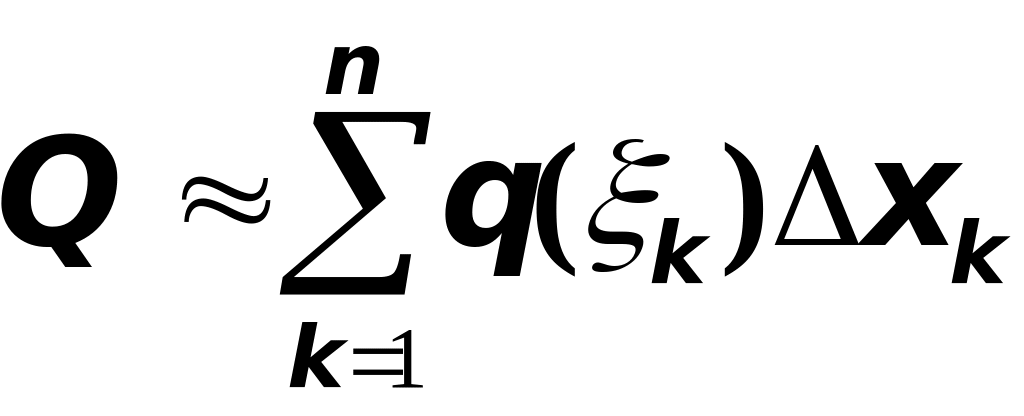 ,
,
тем более точно, чем
меньше
.
Стало быть, точное значение
будет служить пределом суммы при
![]() ,
или, что то же самое,
,
или, что то же самое,
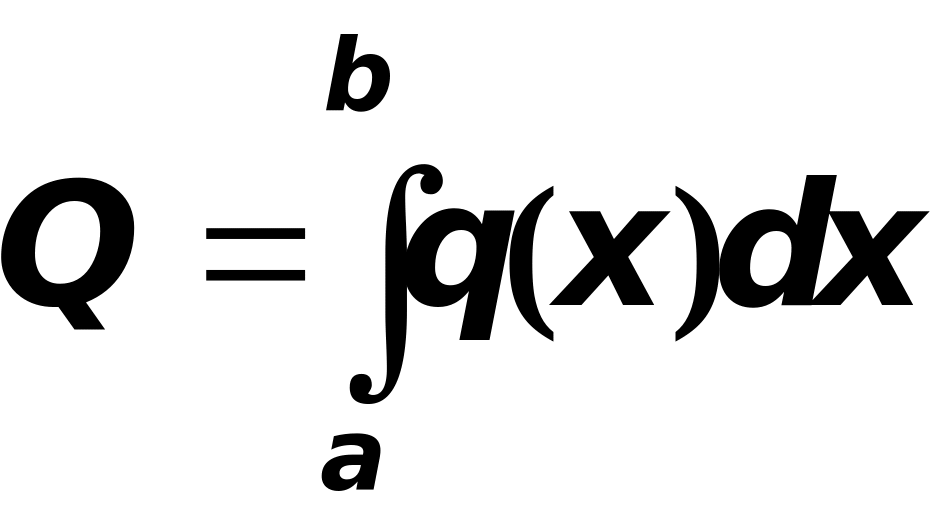 (1)
(1)
На
практике это рассуждение облекают в
более краткую форму, говоря, что если
элемент
![]() величины
,
отвечающий элементарному отрезку
величины
,
отвечающий элементарному отрезку
![]() ,
представим в виде
,
представим в виде
![]() ,
,
т.е.
![]() ,
,
то равенство (1) верно.
