
- •3. Вычисление площади поверхности тела вращения
- •4. Вычисление объёмов
- •§4. Общая схема применения определённого интеграла
- •1. Методика применения определённого интеграла к решению практических задач.
- •2. Работа переменной силы
- •3. Давление на пластинку, погруженную вертикально в жидкость
- •4. Моменты. Центры масс плоских фигур.
- •5. Приложение определённого интеграла к
2. Работа переменной силы
Задача 1. Какую работу нужно затратить, чтобы выкачать воду из полусферического сосуда радиуса ?
Р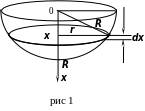 ешение.
Плоскостями, параллельными
плоскости воды, разобьём полушар на
элементы толщины
ешение.
Плоскостями, параллельными
плоскости воды, разобьём полушар на
элементы толщины
![]() (рис 1). Элементарная сила (сила тяжести),
действующая в направлении оси
на слой, толщиной
,
с точностью до бесконечно малых высших
порядков относительно
равна
(рис 1). Элементарная сила (сила тяжести),
действующая в направлении оси
на слой, толщиной
,
с точностью до бесконечно малых высших
порядков относительно
равна
![]() ,
гда
,
гда
![]() - плотность воды,
- плотность воды,
![]() - ускорение свободного падения.
Следовательно, элементарная работа
силы равна
- ускорение свободного падения.
Следовательно, элементарная работа
силы равна
![]() ,
,
где
- уровень воды,
![]() ;
отсюда находим
;
отсюда находим
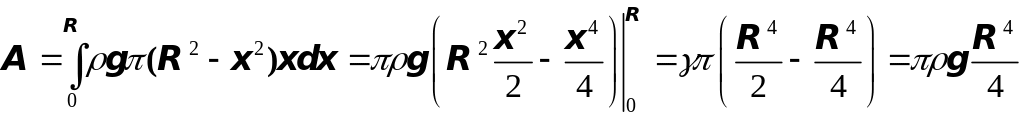 .
.
3. Давление на пластинку, погруженную вертикально в жидкость
Для
вычисления силы давления жидкости
используют закон Паскаля, согласно
которому сила давления жидкости на
пластинку площади
с глубиной погружения
![]() равна
равна
![]() ,
,
где - плотность жидкости, - ускорение свободного падения.
Задача
2. Треугольный щит вертикально
опущен в воду, причём основание
треугольника находится на уровне воды
(рис 2). Требуется найти силу давления
![]() на одну из сторон щита, если щит имеет
форму равностороннего треугольника
.
на одну из сторон щита, если щит имеет
форму равностороннего треугольника
.
Р
рис 2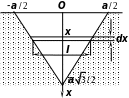 ешение.
Прямыми, параллельными
плоскости воды, разобьём треугольник
на элементы (полоски) ширины
.
Площадь одного такого элемента (отбрасывая
бесконечно малые высшего порядка),
находящегося на расстоянии
от поверхности воды, равна
ешение.
Прямыми, параллельными
плоскости воды, разобьём треугольник
на элементы (полоски) ширины
.
Площадь одного такого элемента (отбрасывая
бесконечно малые высшего порядка),
находящегося на расстоянии
от поверхности воды, равна
![]() .
Из подобия треугольников, изображенных
на рис 2, ясно, что длина
.
Из подобия треугольников, изображенных
на рис 2, ясно, что длина
![]() полоски удовлетворяет соотношению
полоски удовлетворяет соотношению
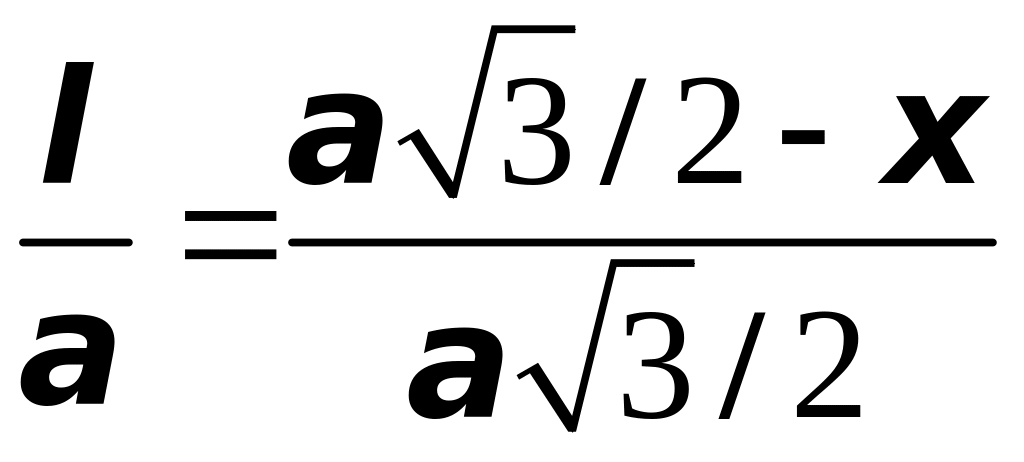 ,
,
откуда
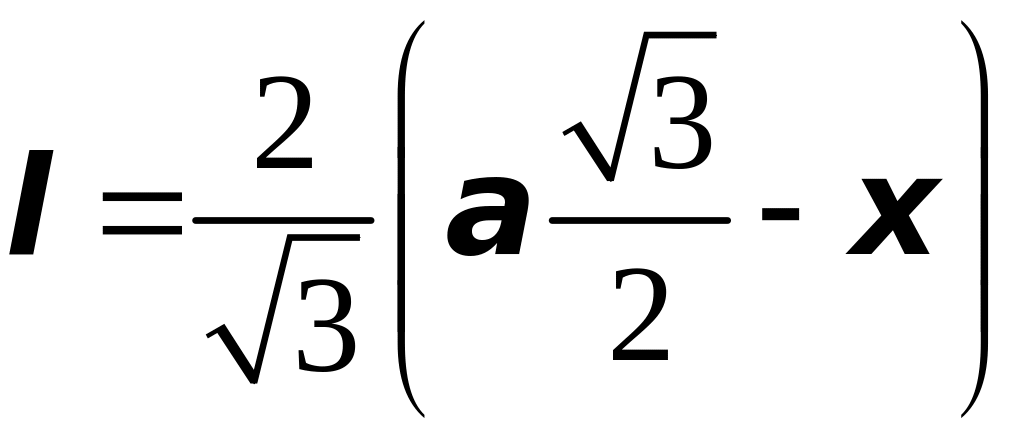 и, следовательно, элементарное давление
и, следовательно, элементарное давление
![]() на полоску ширины
равно
на полоску ширины
равно
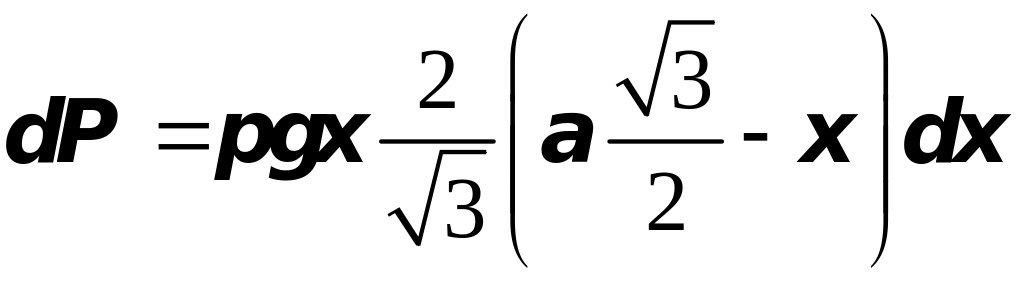 .
Отсюда
.
Отсюда
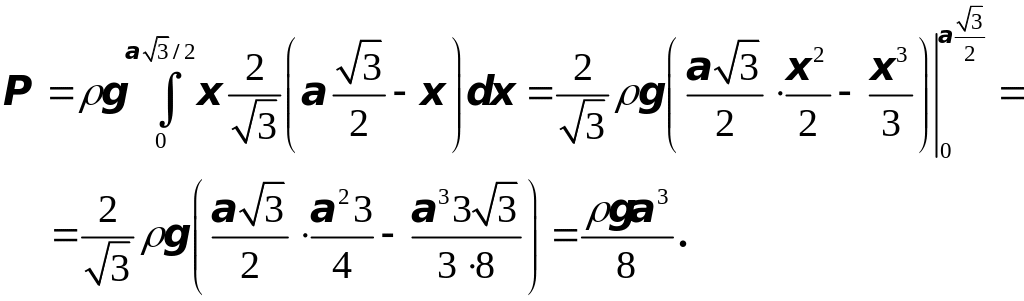
Задача 3. Найти силу давления , испытываемую полукругом радиуса , погруженным вертикально в воду так, что его диаметр совпадает с поверхностью воды (рис 3).
Разобьём площадь полукруга на элементы (полоски) ширины , параллельные поверхности воды.
П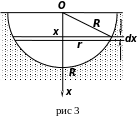 лощадь
одного такого элемента (отбрасывая
бесконечно малые высшего порядка),
находящегося на расстоянии
от поверхности воды, равна
лощадь
одного такого элемента (отбрасывая
бесконечно малые высшего порядка),
находящегося на расстоянии
от поверхности воды, равна
![]() .
.
Сила
давления, испытываемая этим элементом,
равна
![]() ,
где
- плотность воды,
- ускорение свободного падения. Отсюда
вся сила давления есть
,
где
- плотность воды,
- ускорение свободного падения. Отсюда
вся сила давления есть
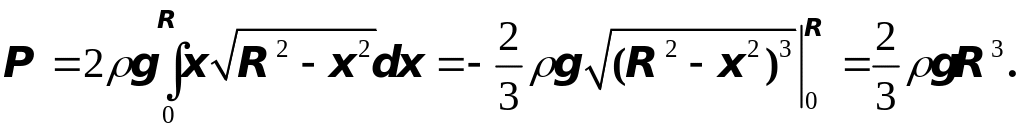
4. Моменты. Центры масс плоских фигур.
Моментом
инерции относительно оси
материальной точки
,
имеющей массу
![]() и отстоящей от оси
на расстояние
и отстоящей от оси
на расстояние
![]() ,
называется величина
,
называется величина
![]() .
.
Моментом
инерции относительно оси
системы
материальных точек с массами
![]() называется сумма
называется сумма
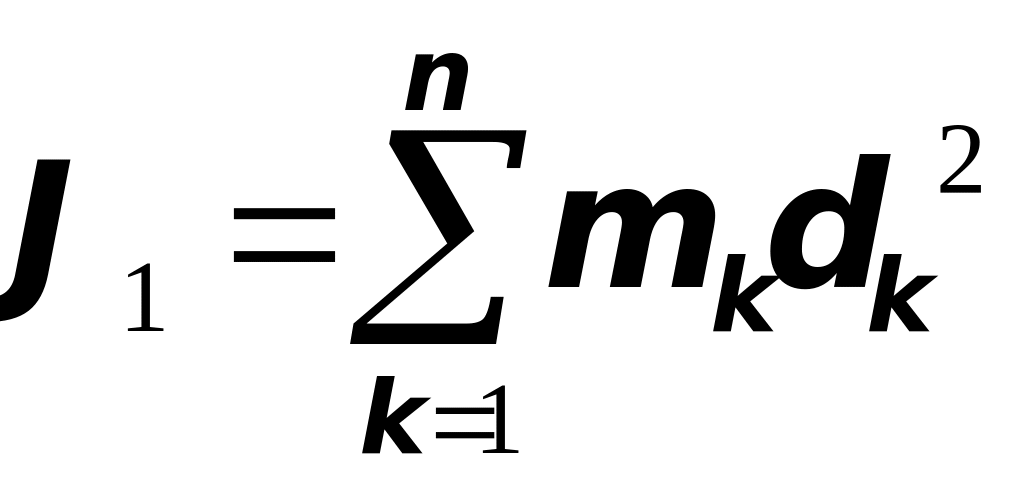
где
![]() - расстояния точек до оси
.
В случае сплошной массы, распределённой
в плоской области, вместо суммы должен
быть соответствующий интеграл.
- расстояния точек до оси
.
В случае сплошной массы, распределённой
в плоской области, вместо суммы должен
быть соответствующий интеграл.
Задача
4. Найти момент инерции
однородной пластинки, имеющей форму
треугольника с основанием
и высотой
,
относительно его основания. Будет
предполагать пластинку однородной, так
что её поверхностная плотность равна
(т.е. масса, приходящаяся на единицу
площади) будет постоянной и, следовательно,
![]() ,
где
- площадь пластинки.
,
где
- площадь пластинки.
Р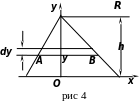 ешение.
За основание треугольника
примем ось
,
а его высоту за ось
(рис 4). Разобьём треугольник на бесконечно
тонкие горизонтальные полоски ширины
ешение.
За основание треугольника
примем ось
,
а его высоту за ось
(рис 4). Разобьём треугольник на бесконечно
тонкие горизонтальные полоски ширины
![]() ,
играющие роль элементарных масс
,
играющие роль элементарных масс
![]() .
.
Используя подобие треугольников получаем:
![]() .
.
Площадь
![]() бесконечно тонкой горизонтальной
полоски ширины
равна
бесконечно тонкой горизонтальной
полоски ширины
равна
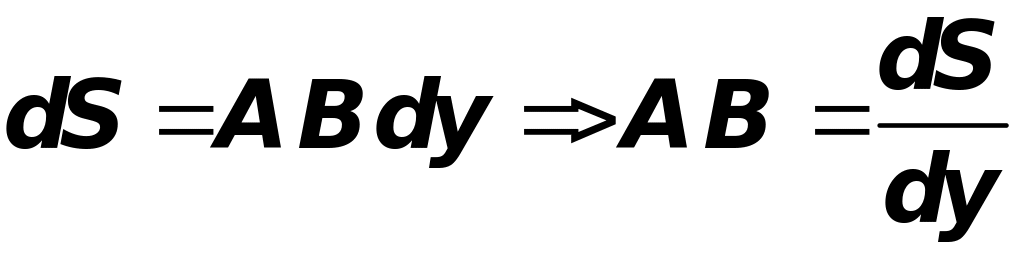 ,
тогда получим
,
тогда получим
 ,
,
откуда
![]() .
.
Следовательно,
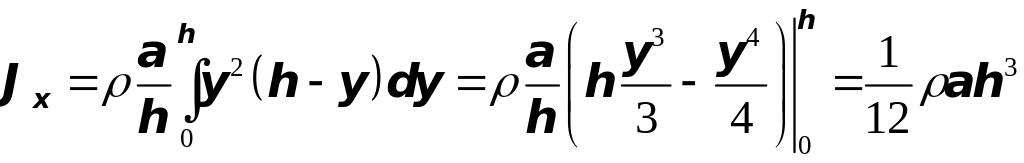 .
.
Статическим
моментом относительно оси
материальной точки
,
имеющей массу
и отклонение
(с учётом знака) оси
,
называется величина
![]() .
.
Статическим
моментом относительно оси
системы
материальных точек с массами
![]() ,
лежащих в одной плоскости с осью
и имеющих отклонения
,
лежащих в одной плоскости с осью
и имеющих отклонения
![]() (с учётом знаков) от этой оси (рис 5)
называется сумма
(с учётом знаков) от этой оси (рис 5)
называется сумма
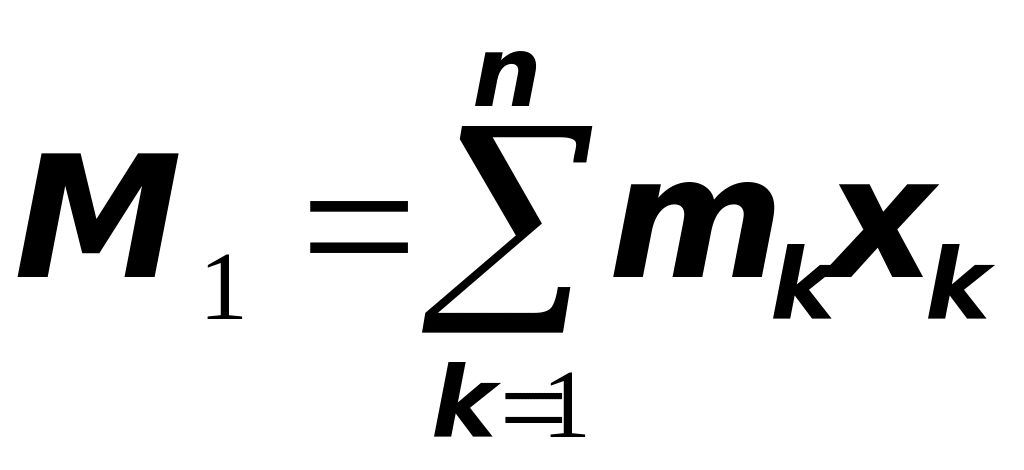 .
.
Если массы непрерывно заполняют фигуру плоскости , то вместо сумм должен быть соответствующий интеграл.
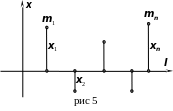
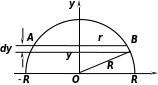
рис 6
Задача 5. Найти статический момент однородной пластинки, имеющей форму полукруга радиуса и плотность , относительно основания полукруга.
Решение.
Основание полукруга поместим
на ось
,
а за ось
примем перпендикуляр к оси
,
проходящий через центр полукруга (рис
6). Разобьём полукруг на бесконечно
тонкие горизонтальные полоски ширины
.
Элементарный статический момент
![]() этой бесконечно тонкой полоски
относительно оси
будет равен
этой бесконечно тонкой полоски
относительно оси
будет равен
![]() ,
следовательно,
,
следовательно,
![]() .
.
Из
треугольника (рис 6) по теореме Пифагора
находим
![]() .
.
Следовательно,
![]() .
.
Интегрируя это равенство по , получим:
 .
.
Координаты
центра масс
![]() плоской фигуры массы
вычисляются по формулам
плоской фигуры массы
вычисляются по формулам
![]()
где
![]() и
и
![]() - статические моменты плоской фигуры
массы
.
- статические моменты плоской фигуры
массы
.
Задача 6. Найти координаты центра масс однородной пластинки, рассмотренной в предыдущем примере.
Р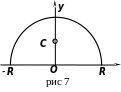 ешение.
Так как пластинка предполагается
однородной (плотность
),
то в силу симметрии пластинки её центр
масс
должен лежать на оси
,
т.е.
ешение.
Так как пластинка предполагается
однородной (плотность
),
то в силу симметрии пластинки её центр
масс
должен лежать на оси
,
т.е.
![]() (рис. 7).
(рис. 7).
Масса пластинки равна
![]()
а так
как из предыдущего примера известно,
что
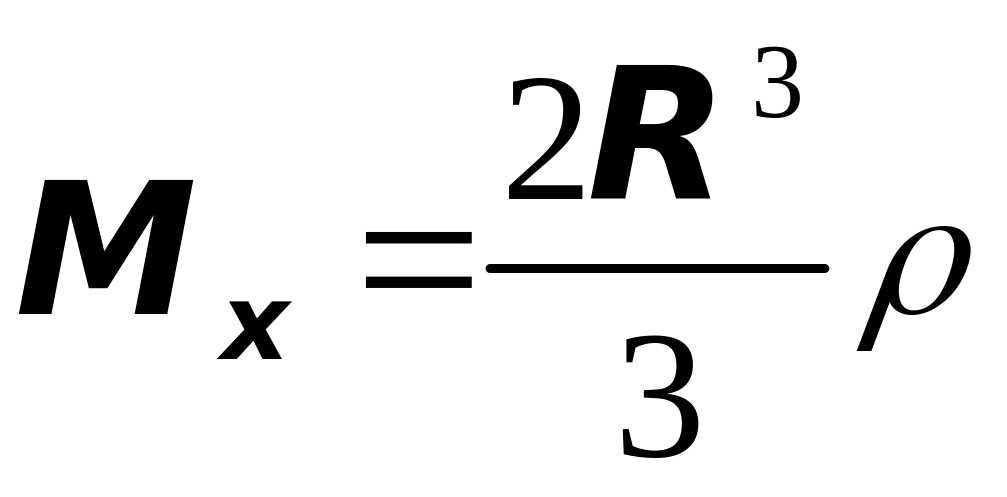 ,
то будем иметь
,
то будем иметь
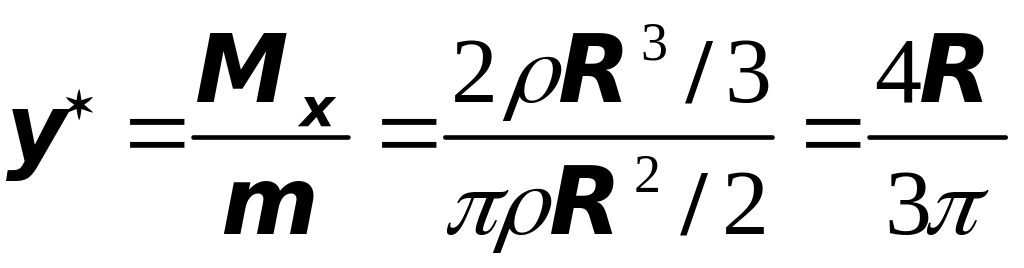 .
Итак,
.
Итак,
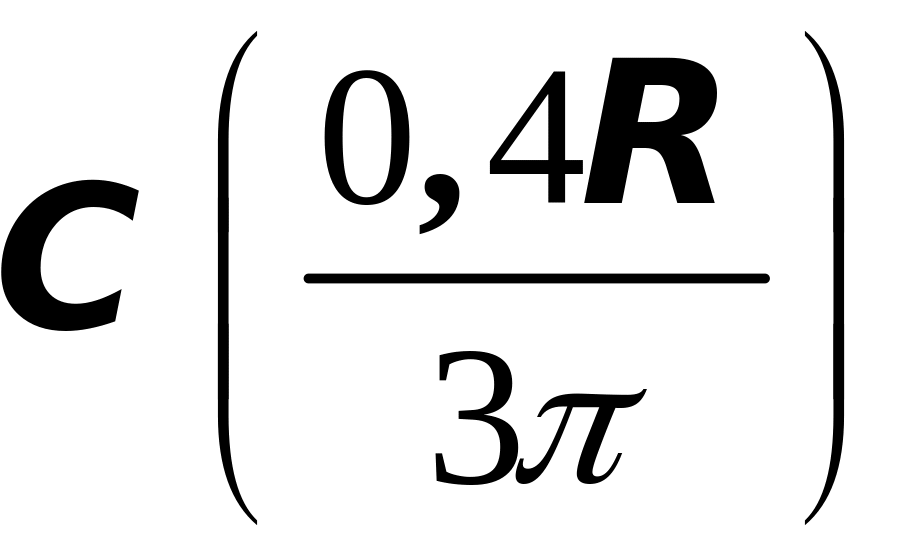 - центр масс однородного полукруга
радиуса
.
- центр масс однородного полукруга
радиуса
.
